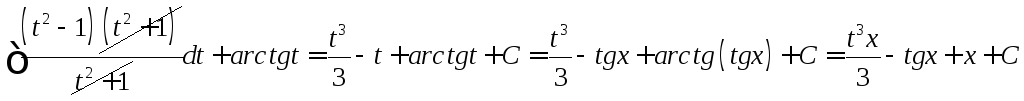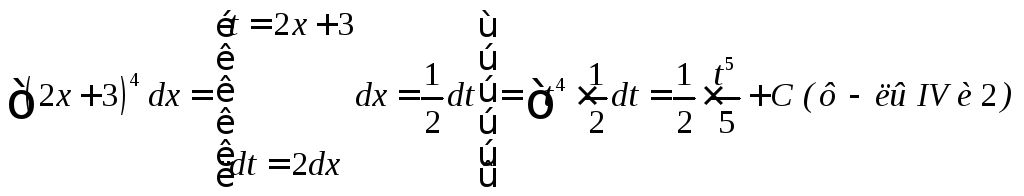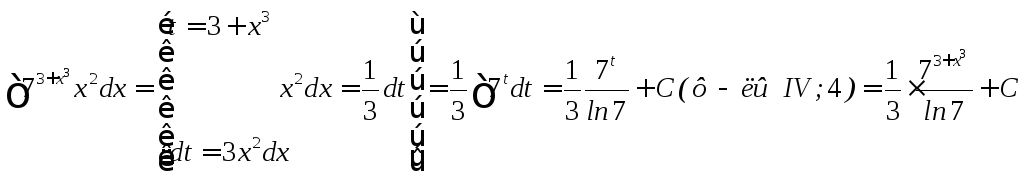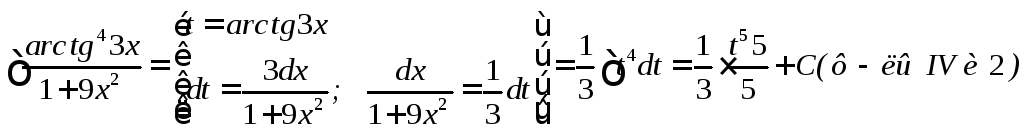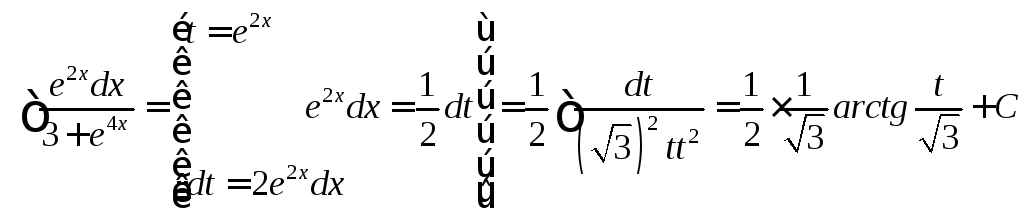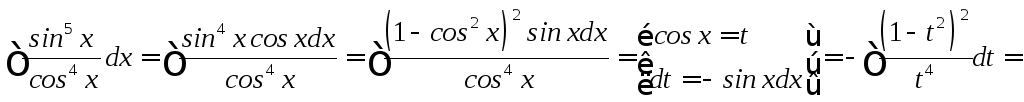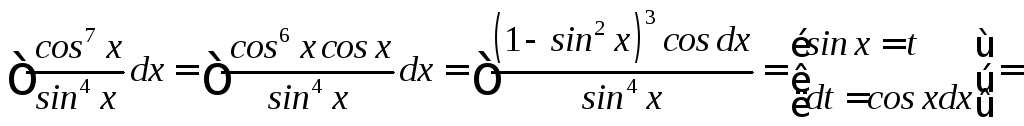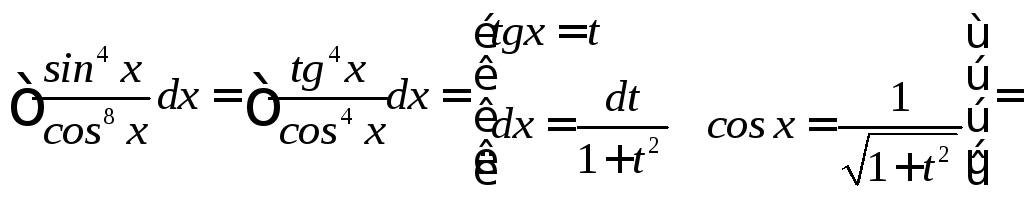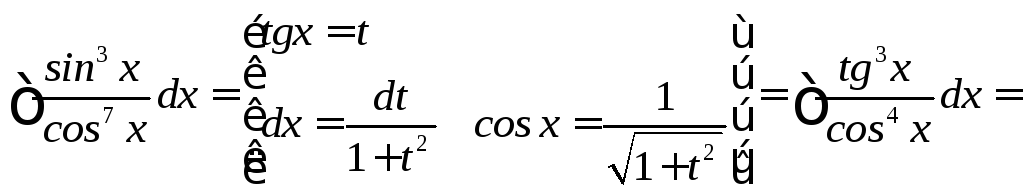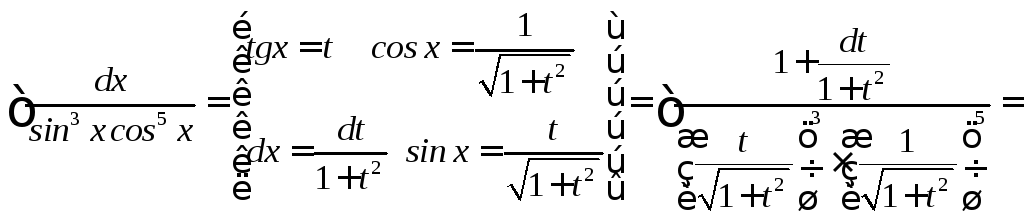- •Высшая математика конспект лекций
- •1 Курс, 2 семестр
- •Содержание
- •Тема 6 «Функции нескольких переменных» 7
- •Тема 7 «Комплексные числа. Многочлены» 13
- •Тема 8 «Неопределённый интеграл» 19
- •Тема 9 «Определенный интеграл» 38
- •Тема 10 «Приложения определенного интеграла» 43
- •Тема 11 «Дифференциальные уравнения» 48
- •Введение
- •Тематический план
- •Предел функции двух переменных.
- •Частные производные первого порядка
- •Градиент функции. Производная по направлению вектора.
- •Вопросы для самоконтроля
- •Тема 7 «Комплексные числа. Многочлены» Основные понятия
- •Действия с комплексными числами
- •Рациональные дроби. Краткие сведения из теории многочленов.
- •Рациональные дроби.
- •Вопросы для самоконтроля
- •Тема 8 «Неопределённый интеграл» Первообразная функция. Основная теорема о первообразных
- •Понятие неопределенного интеграла
- •Основные свойства неопределенного интеграла
- •Инвариантность формул интегрирования
- •Метод непосредственного интегрирования
- •Метод замены переменной (способ подстановки)
- •Интегрирование по частям
- •Интегралы от некоторых функций, содержащих квадратный трехчлен
- •Интегрирования рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Интегралы от дифференциальных биномов
- •Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
- •Вопросы для самоконтроля
- •Тема 9 «Определенный интеграл» Понятие определённого интеграла.
- •Основные свойства определённого интеграла.
- •Вопросы для самоконтроля
- •Тема 10 «Приложения определенного интеграла» Вычисление площадей плоских фигур
- •Вычисление объема тела
- •Обыкновенные дифференциальные уравнения 1-го порядка.
- •Условие (5) называется начальным условием.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •Нетрудно заметить, что уравнение (21) представляет собой уравнение с разделяющимися переменными, метод решения которого изложен в лекции 1.
- •Уравнение Бернулли Уравнением Бернулли называется уравнение вида:
- •Геометрические задачи.
- •Пример 7.
- •Решение
- •Дифференциальные уравнения высших порядков.
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Решить дифференциальное уравнение:
- •Пример 10.
- •Линейные дифференциальные уравнения порядка n
- •Решение линейных неоднородных уравнений
- •Решение однородных уравнений.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.
- •Укажем частные решения , соответствующие различным простейшим случаям специальной правой части:
- •Пример. (Задача типа 61-70).
- •Решение
- •Вопросы для самоконтроля
- •Литература
Метод непосредственного интегрирования
Непосредственным интегрированием называется интегрирование, заключающиеся в непосредственном применении формул таблице основных интегралов.
Чтобы найти неопределенный интеграл от какой-нибудь функцииf (x) нужно прежде всего отыскать в таблице интегралов формулу в левой части которой стоит интеграл того же вида, как данный и записать ответ в соответствии с правой частью равенства.
Примеры
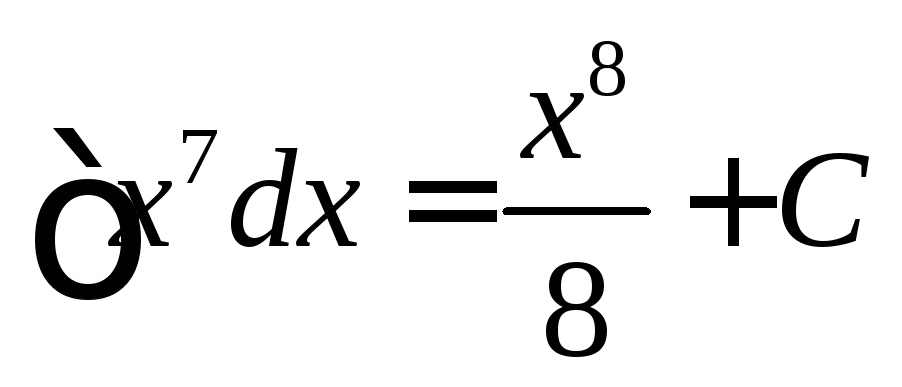 (формула
2)
(формула
2)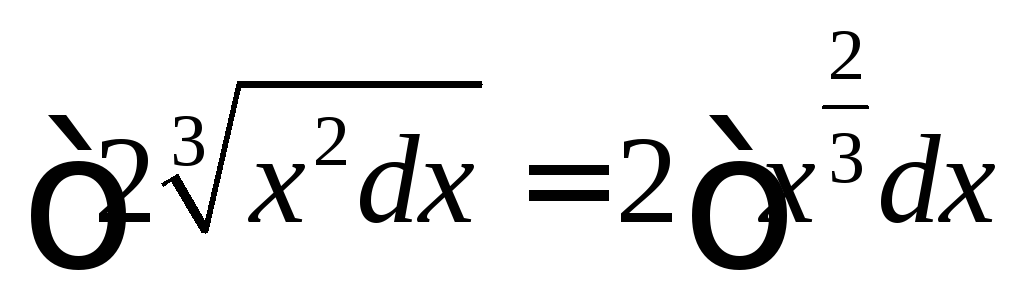 (формула
IV)
(формула
IV)
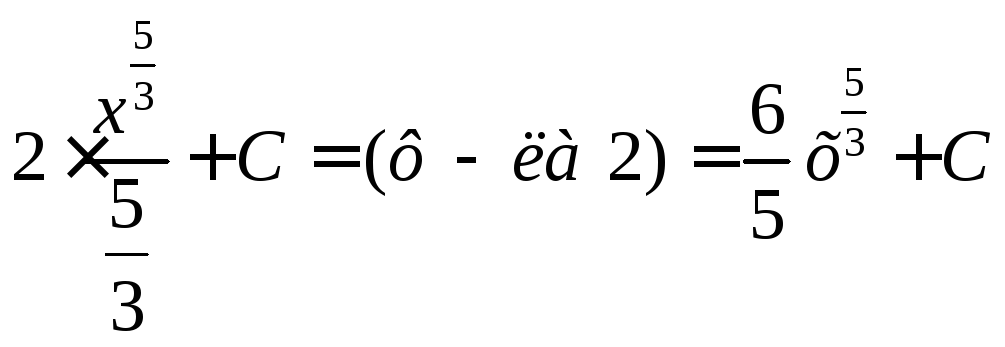
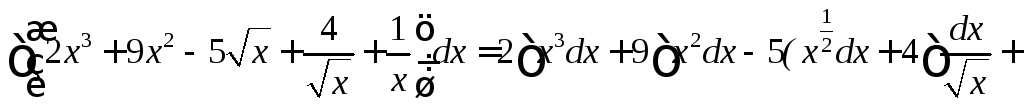
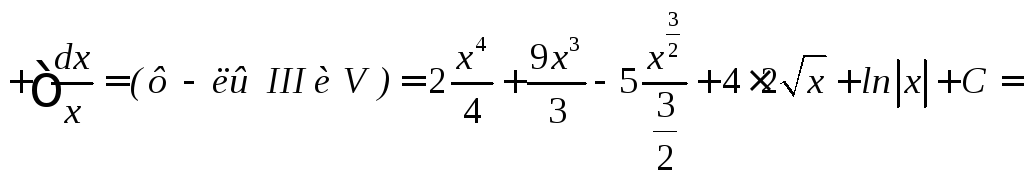
![]()
При вычислении неопределенных интегралов полезно помнить следующие правила:
Если
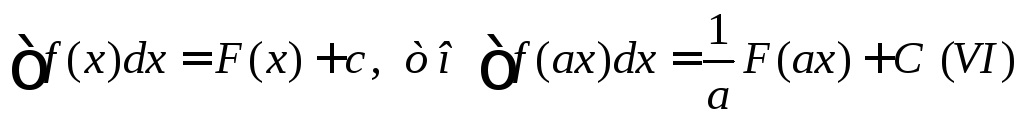
![]()
Если
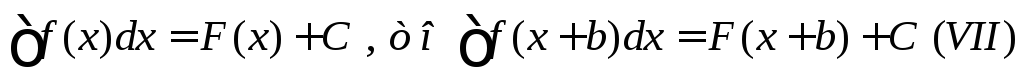
![]()
Если
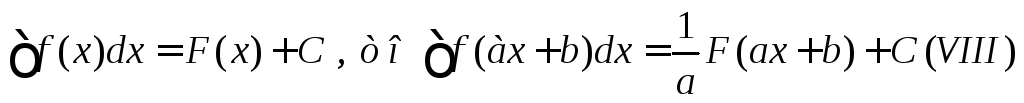
![]()
Если числитель подинтегральной функции является производной знаменателя, то интеграл равен логарифму знаменателя
![]()
Примеры
![]()
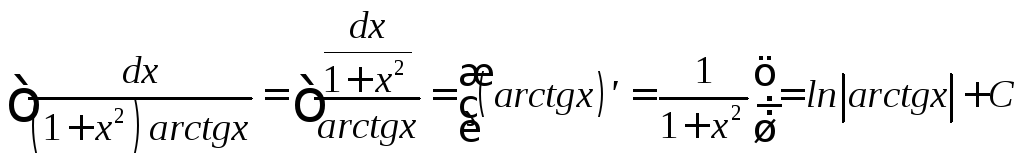
Метод замены переменной (способ подстановки)
Наиболее
общим приемом интегрирования функций
является способ подстановки, который
применяется тогда. Когда искомый интеграл
![]() не является табличным, но путем
преобразований может быть сведен к
табличному.
не является табличным, но путем
преобразований может быть сведен к
табличному.
Метод основан на применении следующей формулы:
![]()
где x = φ (t) – дифференцируемая функция от t; причем x = φ (t) - строго монотонна для рассматриваемых значений переменной.
В этом методе мы переменную х заменяем x = φ (t) dx = φ| (t) dt
Примеры
![]()
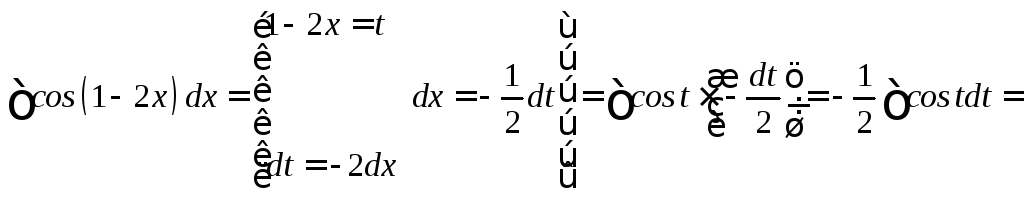
![]()
![]()
![]()
Интегрирование по частям
Пусть
u
и v
– две дифференцируемые функции от х.
Тогда, как известно, дифференциал от
произведения вычисляется по формуле
![]() .
.
Проинтегрируем обе части
![]() или
или
![]() -
формула
интегрирования по частям
-
формула
интегрирования по частям
Этой
формулой пользуются, когда
![]() невозможно свести к табличному с помощью
подстановки или труднее найти чес
невозможно свести к табличному с помощью
подстановки или труднее найти чес
![]() .
.
Здесь можно различным образом разбить данное подынтегральноe выражение на множители u и du.
Рассмотрим основные случаи, когда применяется метод интегрирования по частям.
![]()
2)
![]()
![]()
3)
![]()
4)
![]()
![]()
5)

Примеры
1)
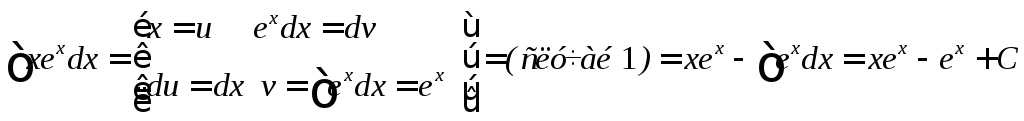
2)
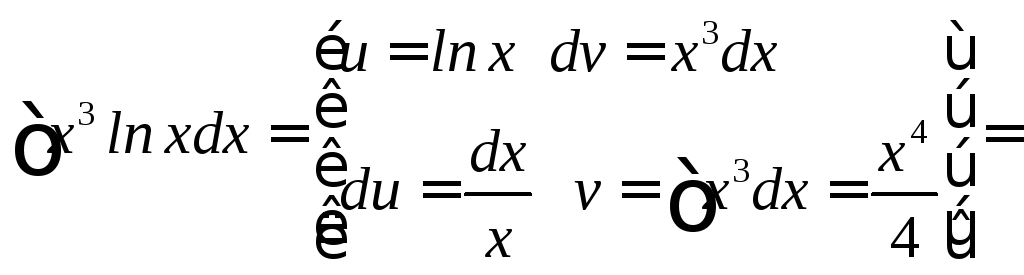
![]()
3)
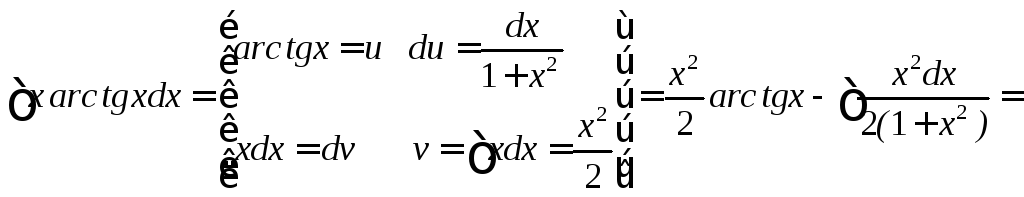
![]()
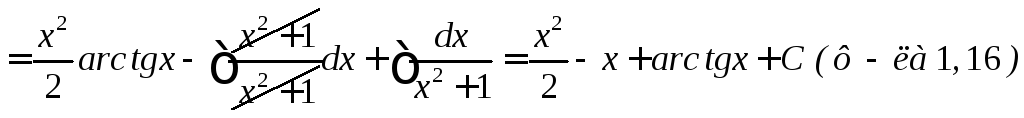
![]()
4)
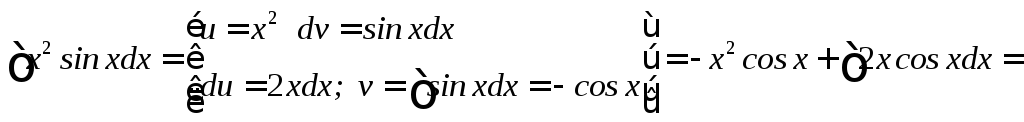
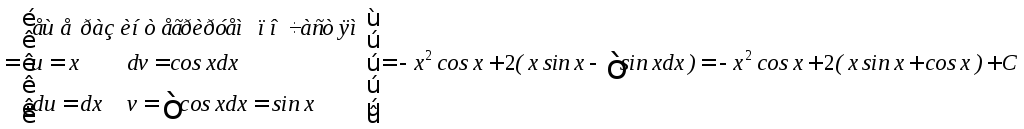
5)

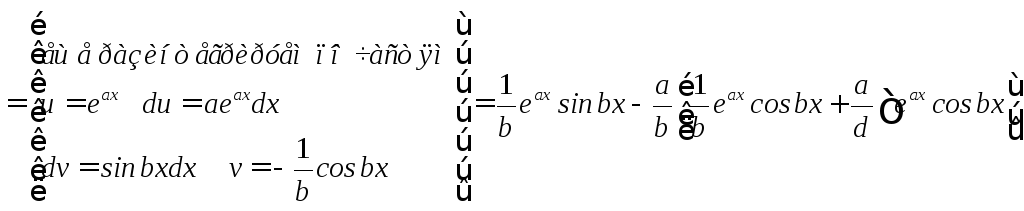
Таким образом, двукратное применение формулы интегрирования по частям приводит к исходному интегралу, который мы вычисляли.
Раскроем скобки в правой части и получим:
![]()
![]()
Отсюда следует, что искомый интеграл равен
![]()
Интегралы от некоторых функций, содержащих квадратный трехчлен
![]()

х
– первое число,
![]() - второе число
- второе число
![]() удвоенное произведение первого на
второе; прибавим и отнимем квадрат
второго числа
удвоенное произведение первого на
второе; прибавим и отнимем квадрат
второго числа
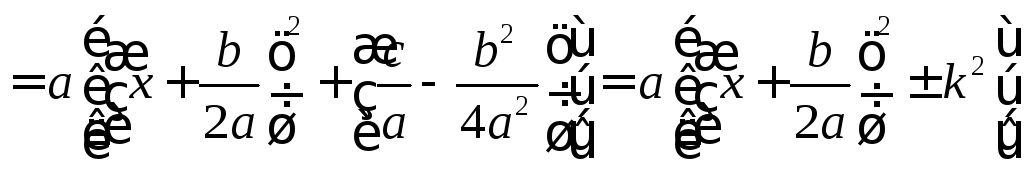
где
![]()
Если
![]()
Имеем
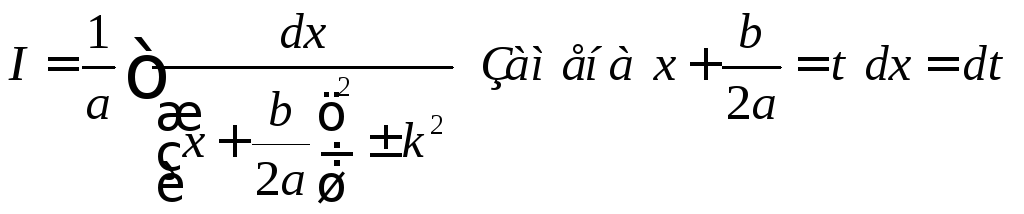
![]()
Примеры
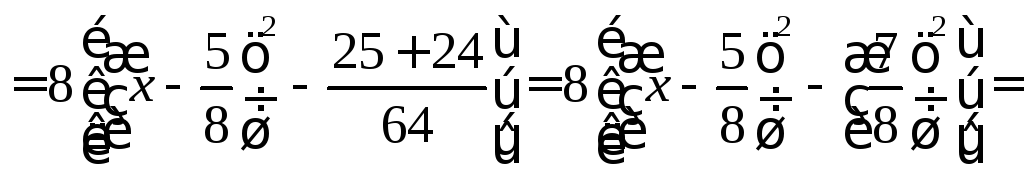
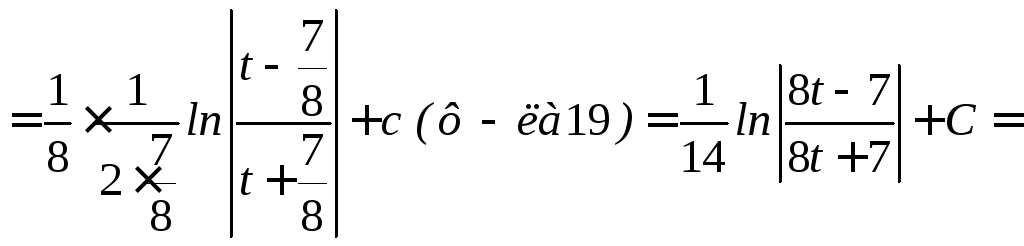
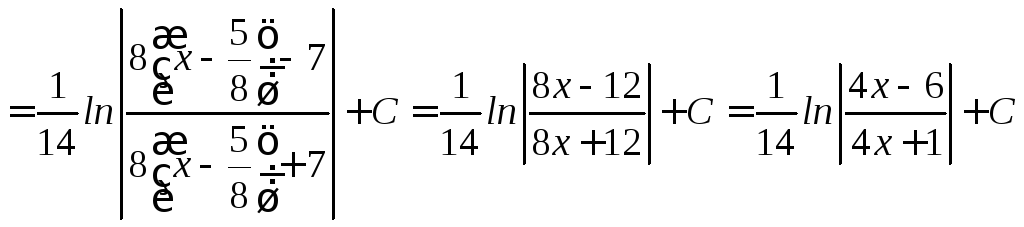
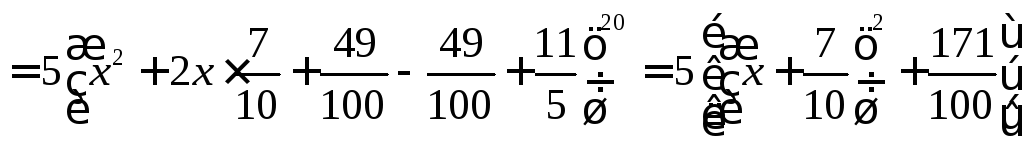
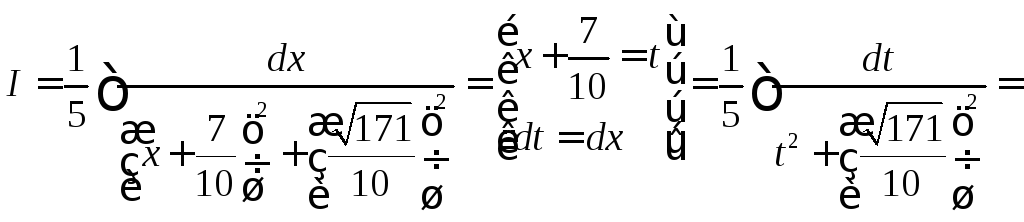
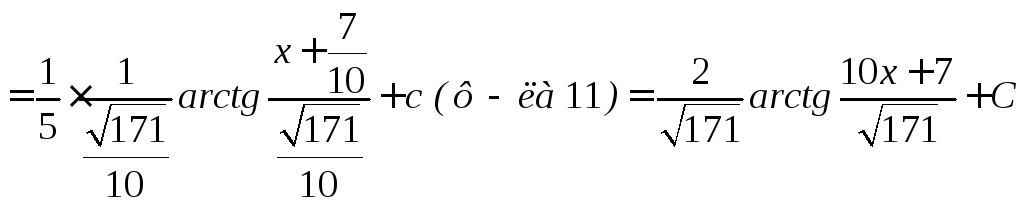
![]()
![]()
![]()
![]()
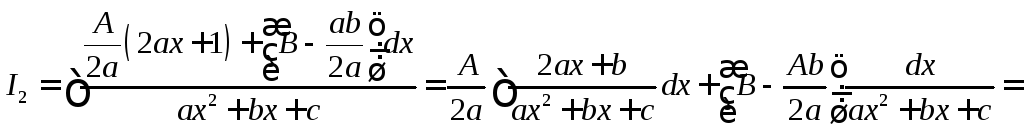
![]()
Пример:
![]()
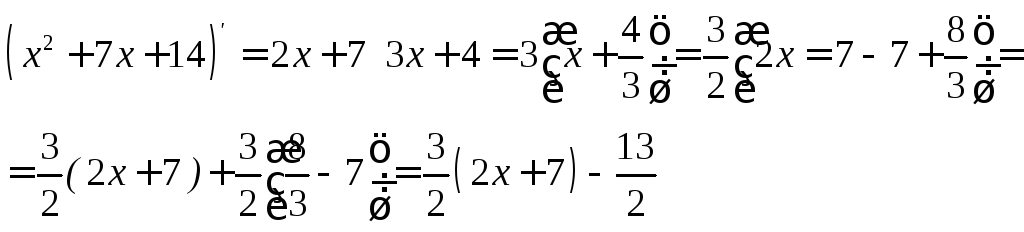
Выделим
полный квадрат:
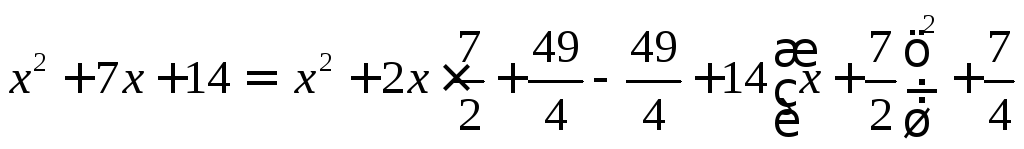
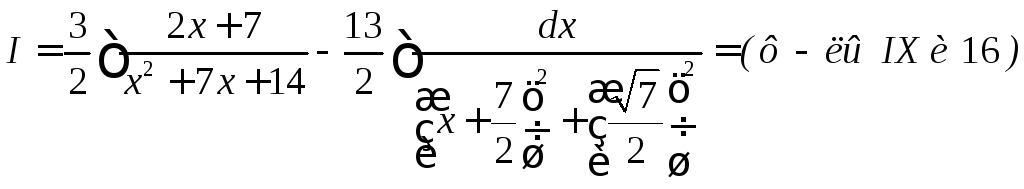
![]()
Интегрирования рациональных дробей
Корни знаменателя действительные и различные.
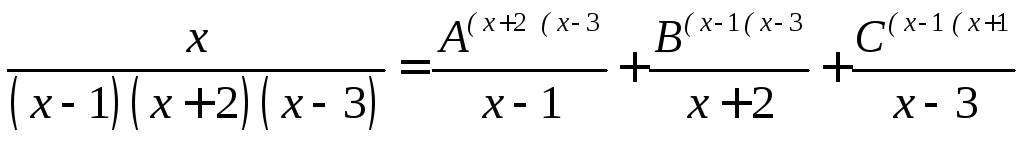
![]()
![]()
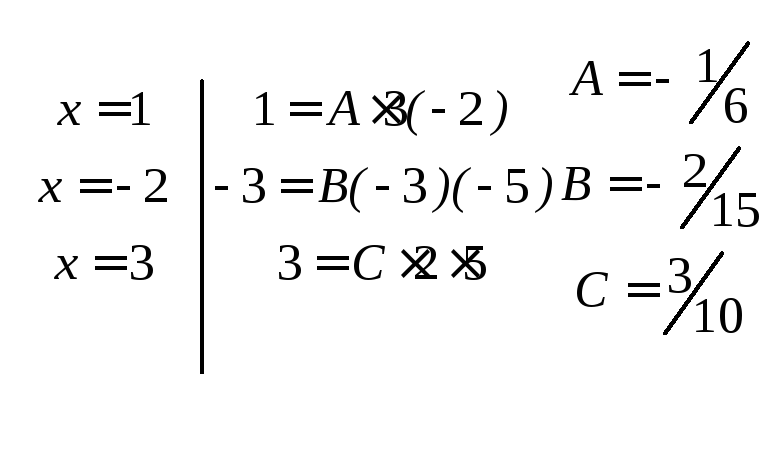
Итак
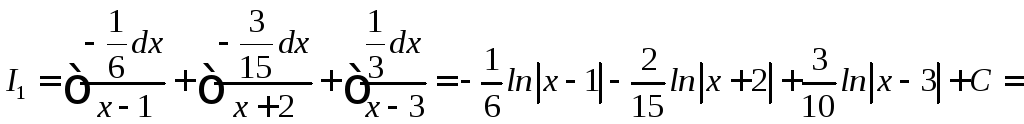
![]()
Корни знаменателя действительные, но среди них есть кратные.
![]() Дробь
неправильная. Выделяем, целую часть
Дробь
неправильная. Выделяем, целую часть
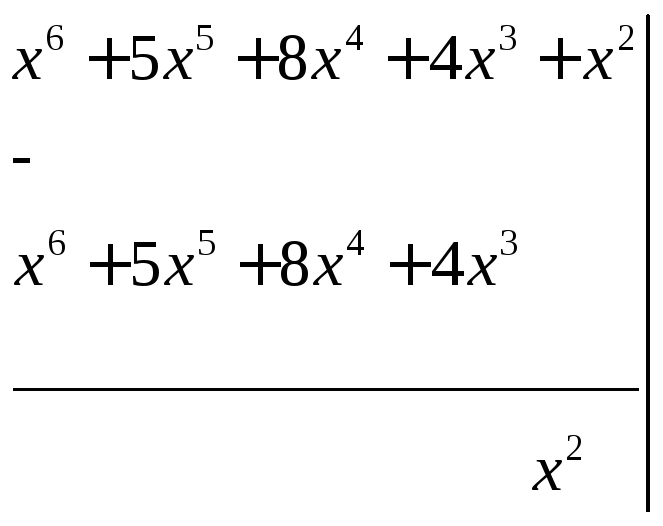
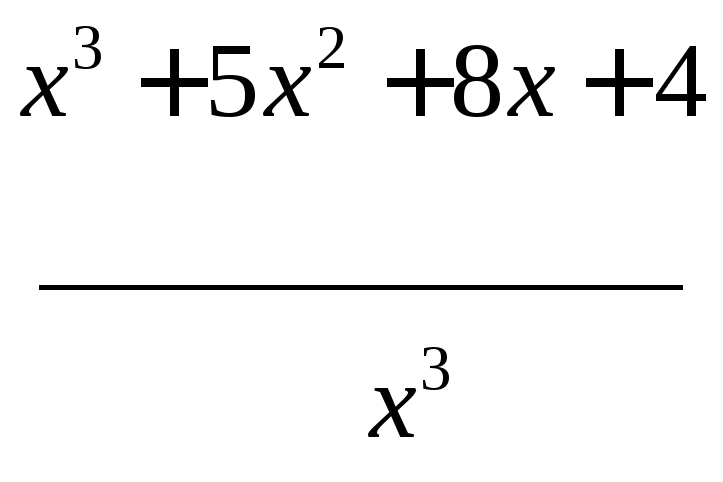
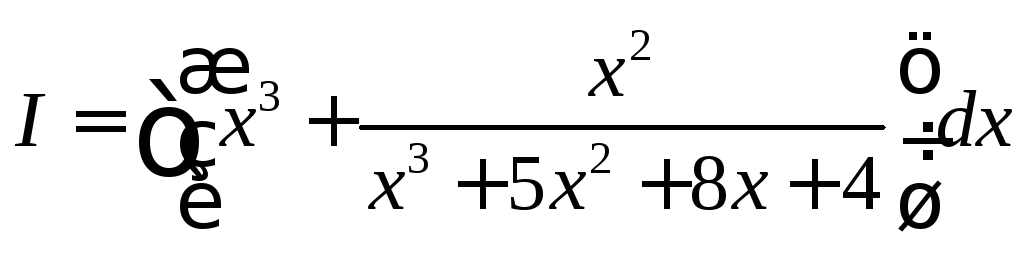
Разложим знаменатель на множители
![]()
![]()
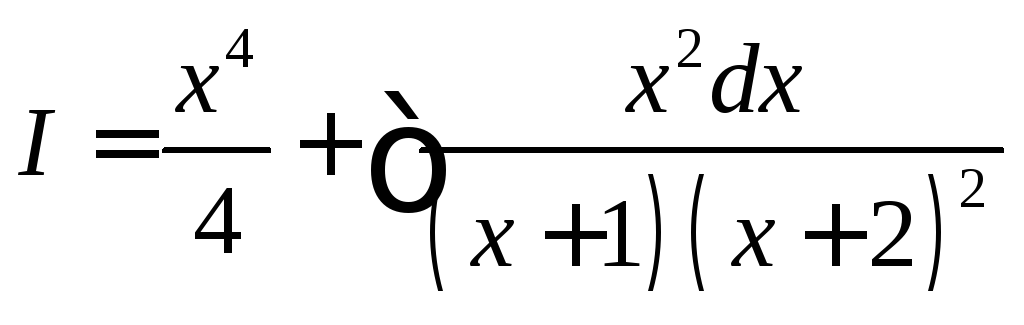 Разложим
дробь на элементарные
Разложим
дробь на элементарные
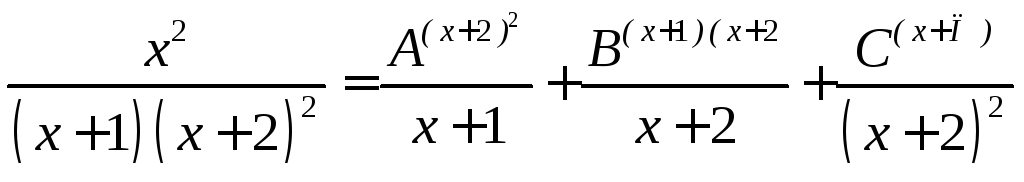
![]()
![]()
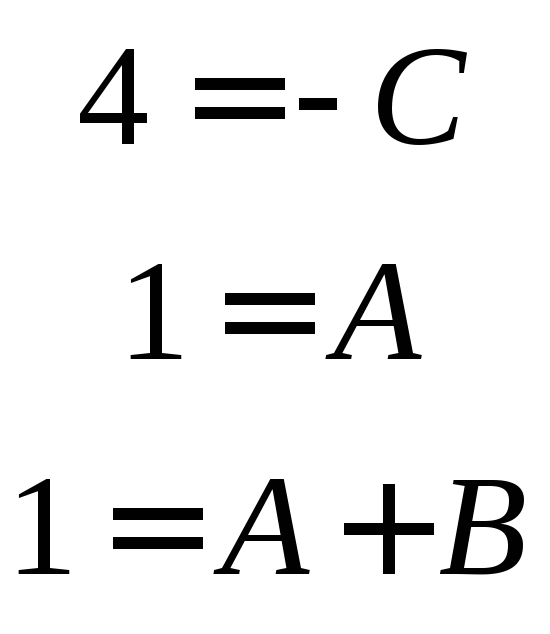
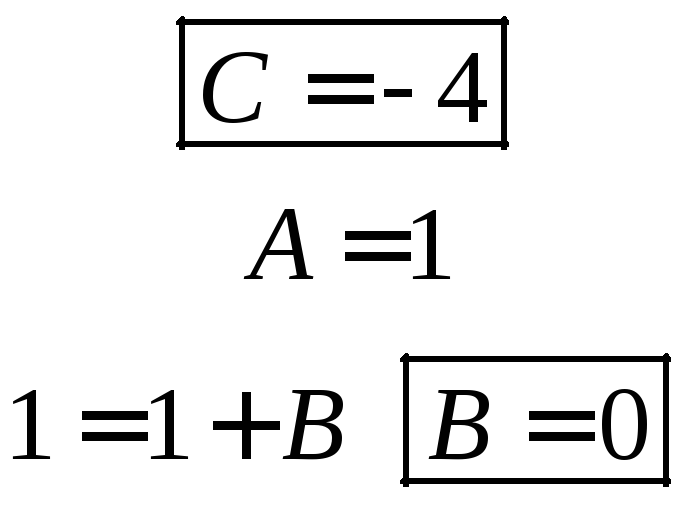
имеем:

Знаменатель имеет кроме действительных корней комплексные или только комплексные.
![]() Дробь
неправильная. Выделим целую часть.
Дробь
неправильная. Выделим целую часть.
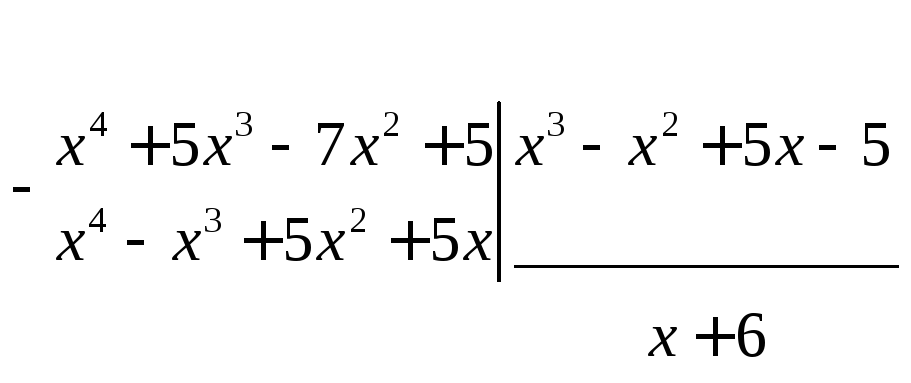
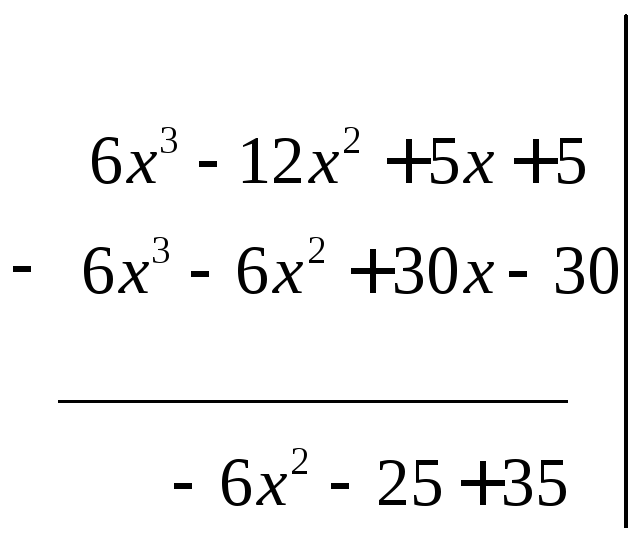
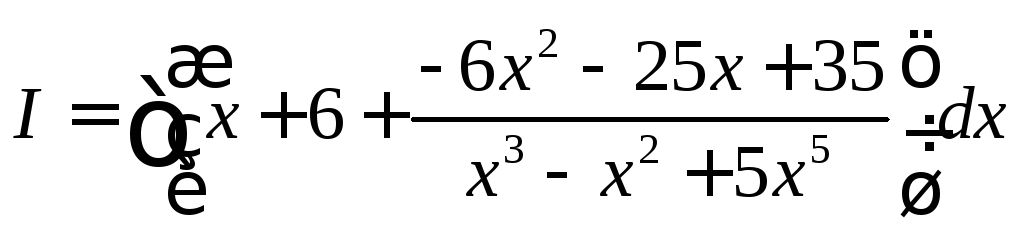
Разложим числитель и знаменатель на множители
![]()
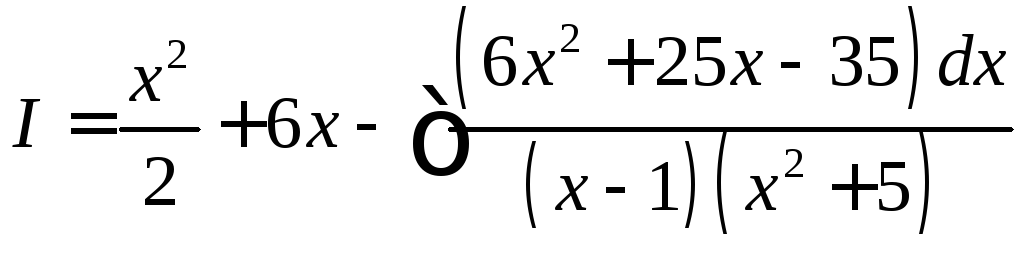 Разложим
дробь на элементарные
Разложим
дробь на элементарные
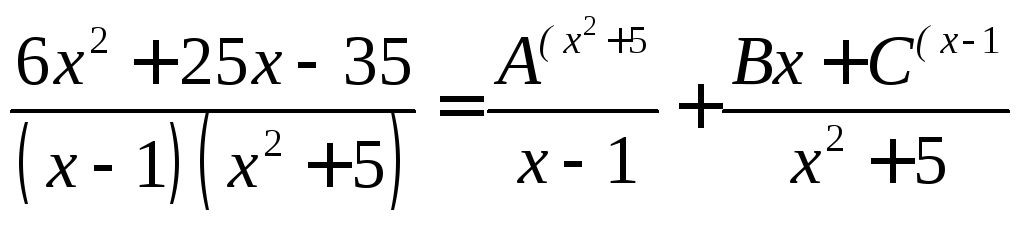
![]()
![]()

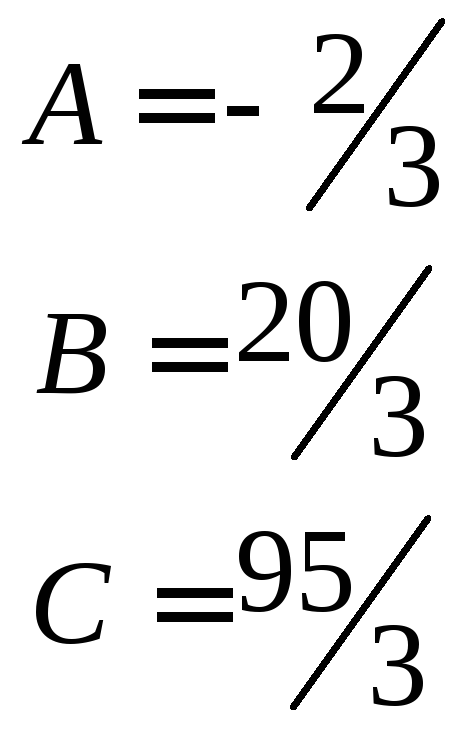
Итак
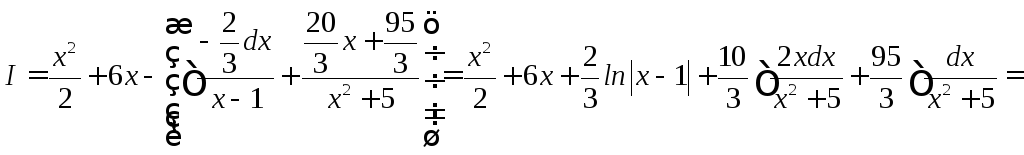
![]()
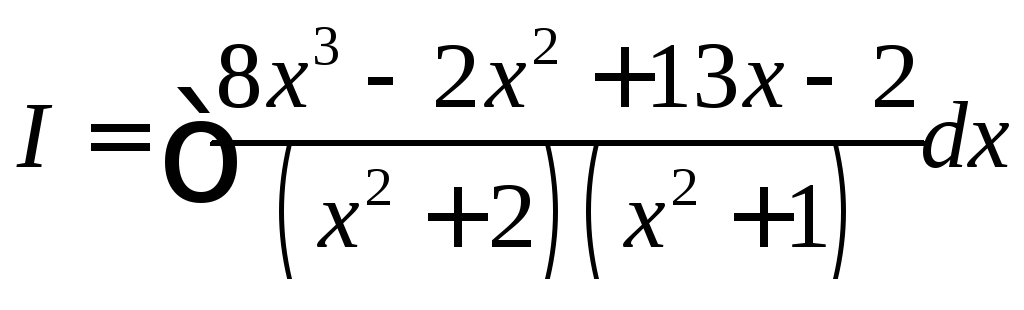 Разобьем
дробь на элементарные
Разобьем
дробь на элементарные
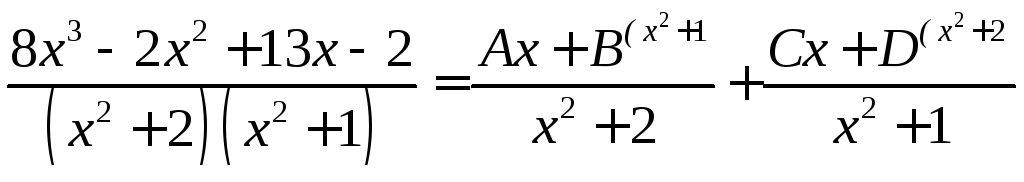
![]()
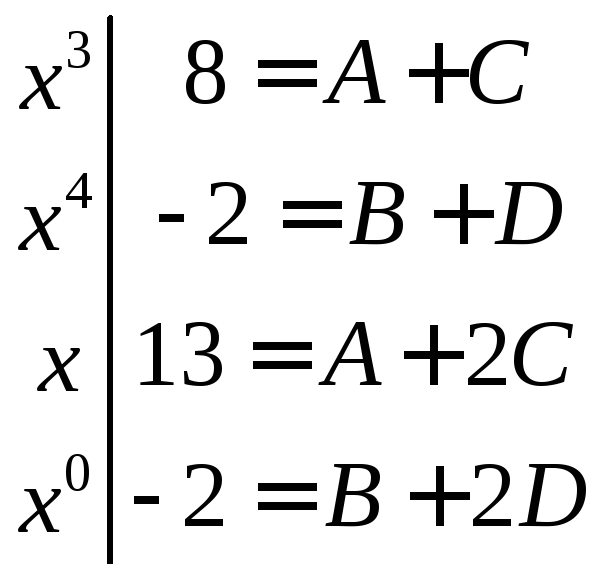
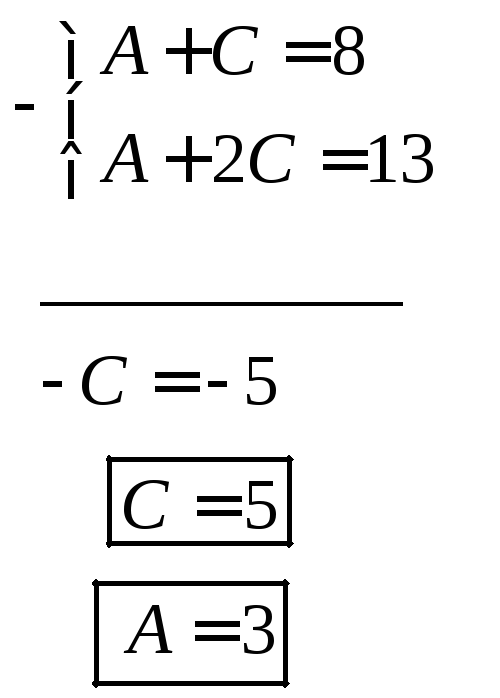
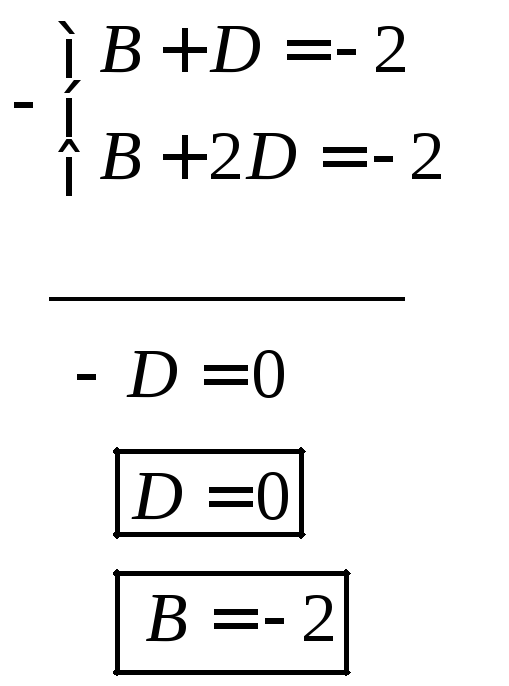
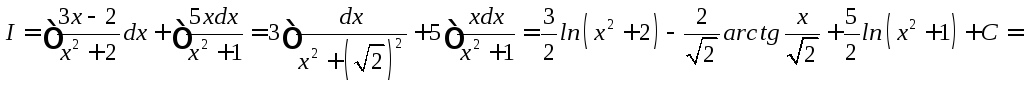
![]()
Интегрирование тригонометрических функций
Интегралы вида
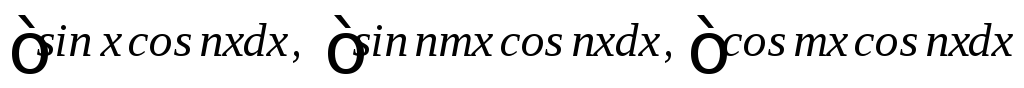 m
и n
целые числа m
≠ n.
m
и n
целые числа m
≠ n.
Интегралы такого типа часть встречаются в приложениях, в частности мы будем ими пользоваться в разделе «Ряды Фурье».
Для вычисления используем формулы
![]() (а)
(а)
![]() (б)
(б)
![]() (в)
(в)
![]()
Пример
![]()
![]()
Интегралы типа,
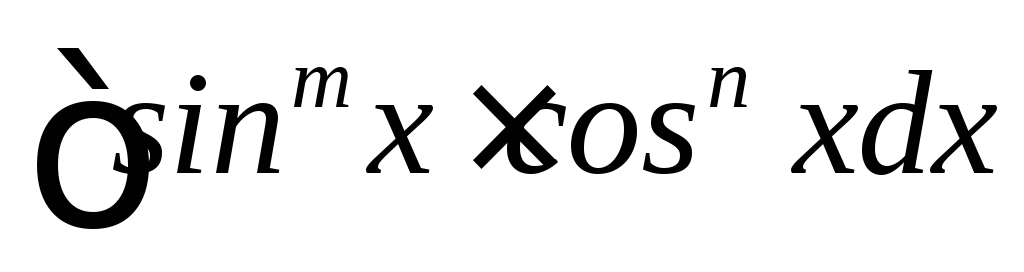 где m
n
– целые числа
где m
n
– целые числа
m > 0; n > 0 причем одно из них нечетное , а другое произвольное.
Пусть m – нечетное, тогда m = 2k + 1
При решении используется формула:
![]()
![]()
![]()
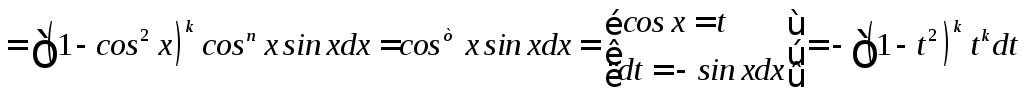
Мы свели интеграл к интегралу от суммы степенных функций
![]()
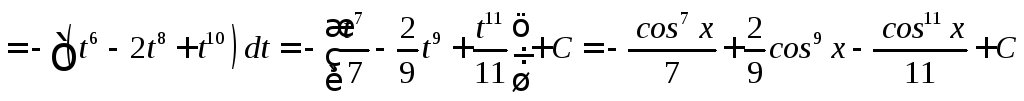
Пусть n – нечетное; n = 2k + 1
![]()
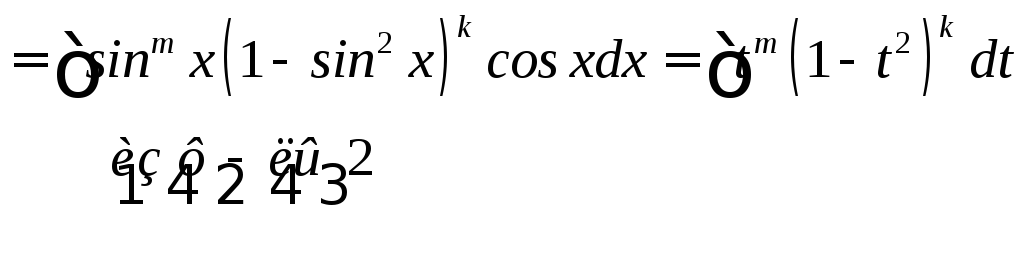
Мы привели интеграл к интегралу от суммы степенных функций
![]()
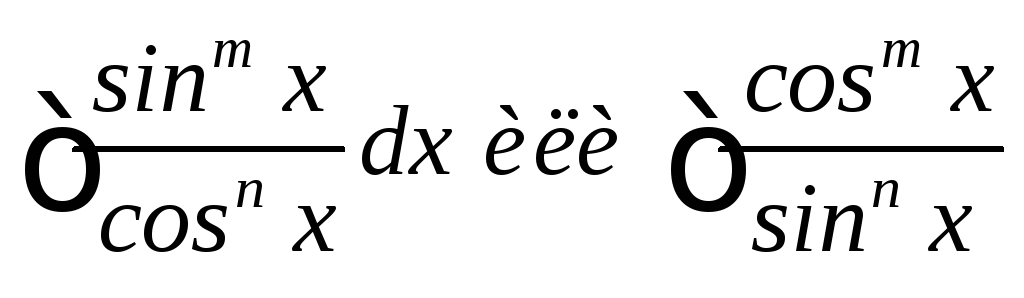 m
– нечетное
m
– нечетное
Подстановка
![]()
![]()
Примеры
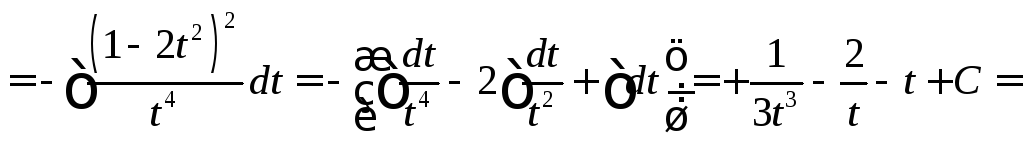
![]()
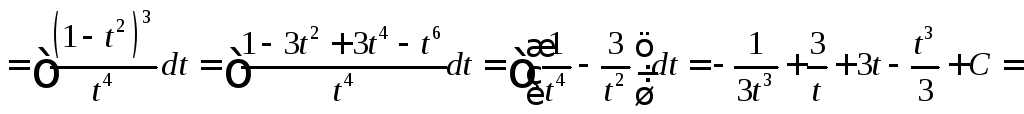
![]()
m > 0, n > 0 оба четные. Берется путем понижения степени с использованием формул:
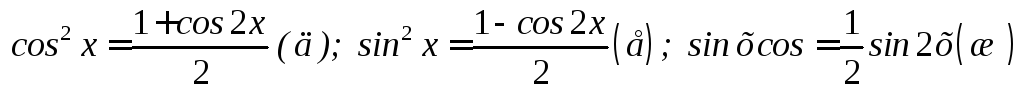
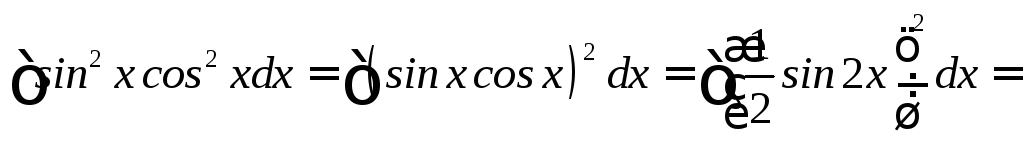
![]()
4 m и n оба четные; одно из них отрицательное
5 m и n – оба нечетные; одно из них отрицательное
6 m и n – отрицательные, а их сумма есть четное число
Подстановка
![]()
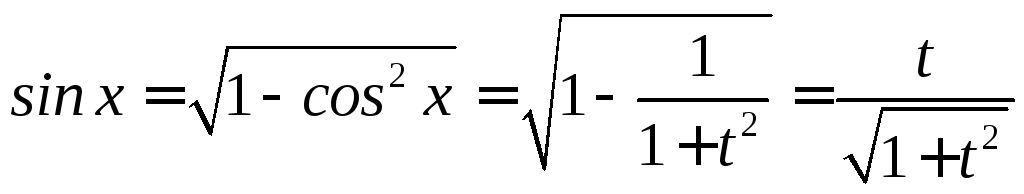
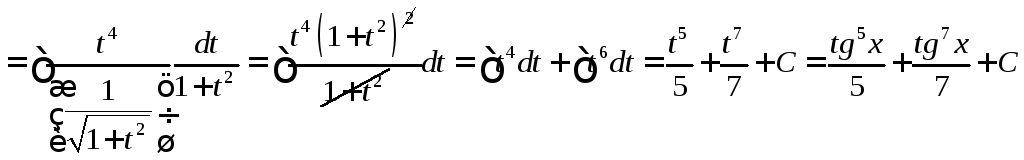
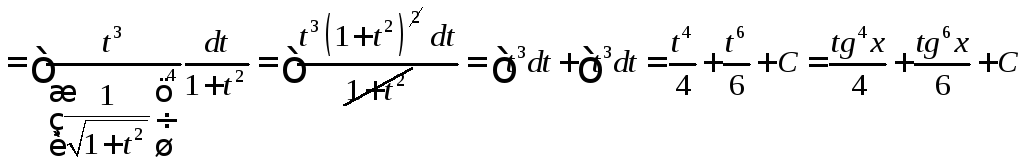
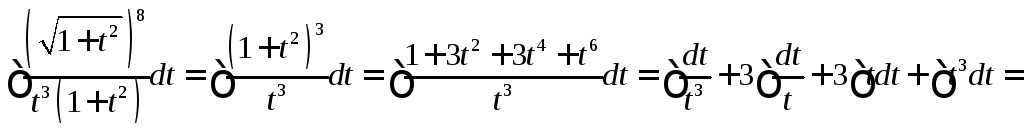
![]()
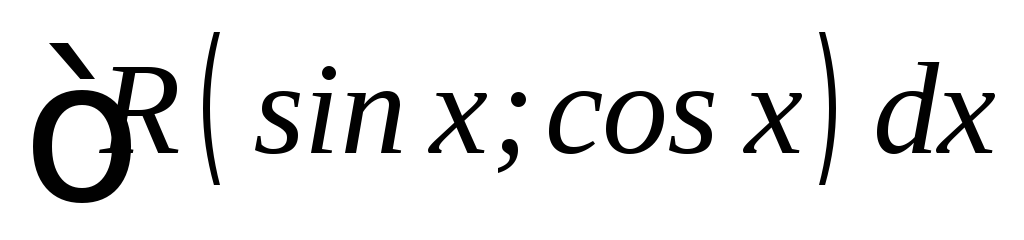 где
R
– рациональная функция х.
где
R
– рациональная функция х.
Если интеграл не сводится к I и II случаям, то применяют универсальную подстановку
![]()
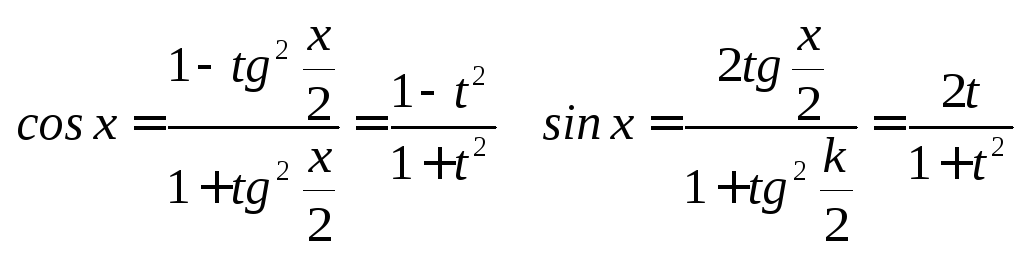
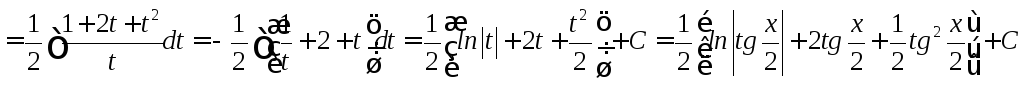
Интегралы вида
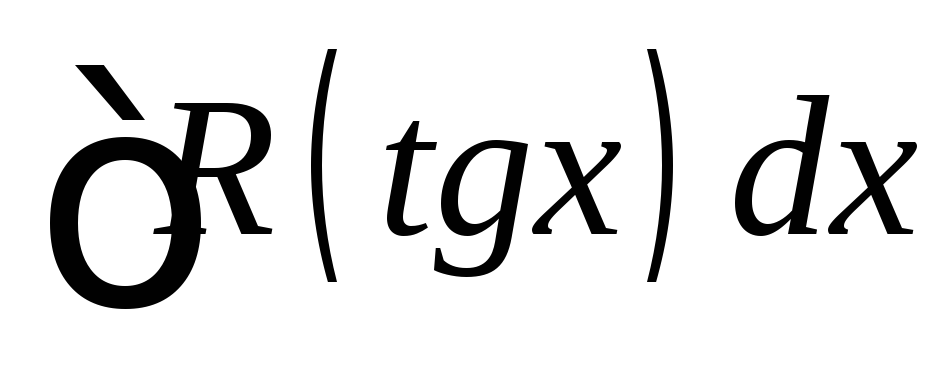
Подстановка
![]()