Тема 7 «Комплексные числа. Многочлены» Основные понятия

Выражение вида , где Х и У – действительные числа, а - мнимая единица, называется комплексным числом в алгебраической форме записи.

Свойства мнимой единицы

Операции над комплексными числами в алгебраической форме зваписи.

Пусть Тогда:

1).

2).

3).

4).

По отношению к операциям сложения и умножения справедливы свойства коммутативности, ассоциативности и дистрибутивности.

5).

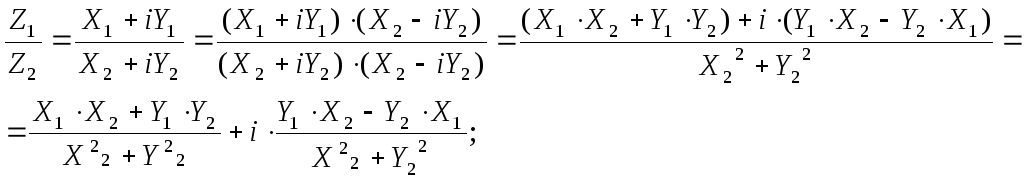
Примеры.

Удобно пользоваться геометрической интерпретацией комплексного числа.

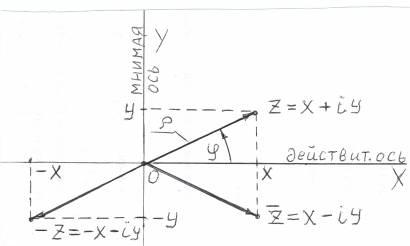
Комплексное число изображают в виде точки комплексной плоскости или радиуса – вектора этой точки. Вектор, симметричный исходному вектору относительно действительной оси ОХ, соответствует комплексному числу, сопряжённому с данным, которое обозначается символом Произведение сопряжённых комплексных чисел - всегда действительное число. Противоположное по отношению к исходному комплексное число на комплексной плоскости изображается как вектор, противоположный данному (он развёрнут на 180 градусов).

Сформулируем общее свойство комплексных чисел.

Действия с комплексными числами

Сумма, разность, произведение, частное комплексных чисел, сопряжённых с исходными, есть комплексное число, сопряжённое с суммой, разностью, произведением, частным исходных комплексных чисел.

Во многих случаях удобнее пользоваться тригонометрической формой комплексного числа. Переход от алгебраической формы комплексного числа к тригонометрической осуществляется на основе простейших формул тригонометрии (см. рисунок).

Здесь: - модуль комплексного числа;

- аргумент – угол, который отсчитывается от действительной оси ОХ в направлении против часовой стрелки (в положительном направлении).

Комплексное число в тригонометрической форме приобретает свойство периодичности. .

Такие математические операции над комплексными числами, как умножение, деление, возведение в степень и извлечение корня удобнее осуществлять, используя тригонометрическую форму комплексных чисел

Пусть

1).

2).

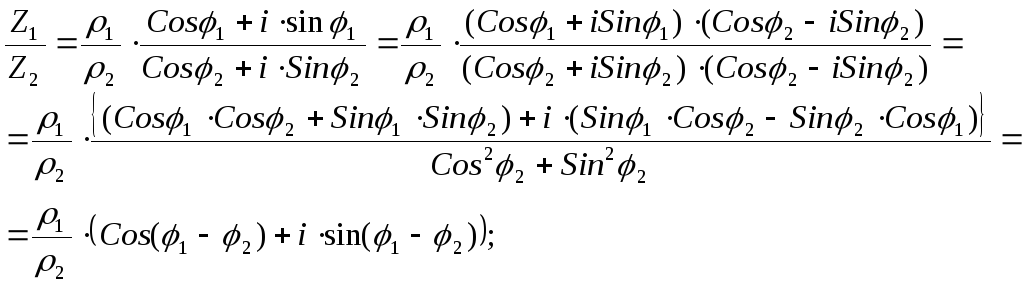
Сформулируем полученное правило.

При перемножении комплексных чисел их модули - перемножаются, а аргументы – складываются. При делении – их модули делятся, а аргументы – вычитаются.

3). Используя формулу 1, запишем формулу для возведения в степень.

(формула Муавра).

4). Извлечение корня из комплексного числа осуществляется по следующему правилу.

Доказательство.

Пусть (формула Муавра).

Но два комплексных числа в тригонометрической форме равны тогда, когда их модули равны, а аргументы отличаются на число, кратное .

Отсюда получим:

Таким образом при извлечении корня из комплексного числа имеем столько корней, какова степень корня.

В теоретических основах электротехники широко используется показательная форма комплексного числа. Переход от тригонометрической формы к показательной осуществляется при помощи формул Эйлера.

Используя эти формулы, получим:

Правила умножения, деления, возведения в степень и извлечения корня из комплексного числа в показательной форме аналогичны правилам для комплексных чисел в тригонометрической форме.

Если то используют формулы.

1).

2).

3).

4).

Пример.

Данное комплексное выражение записать в виде комплексного числа в алгебраической, тригонометрической и показательной формах. Решить уравнение

а)

Решение. , - алгебраическая форма выражения.

Для получения тригонометрической формы найдём модуль и аргумент числа.

Аргумент числа удобно определять, изобразив его на комплексной плоскости.

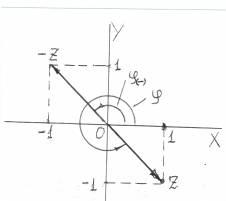
Из рисунка видно что аргумент комплексного числа равен

Тригонометрическая и показательная фоормы имеют вид.

Преобразуем заданное уравнение. Из рисунка видно, что противоположное комплексное число (-Z) имеет тот же модуль, а аргумент его равен Корни уравнения находим по вышеприведённой формуле.

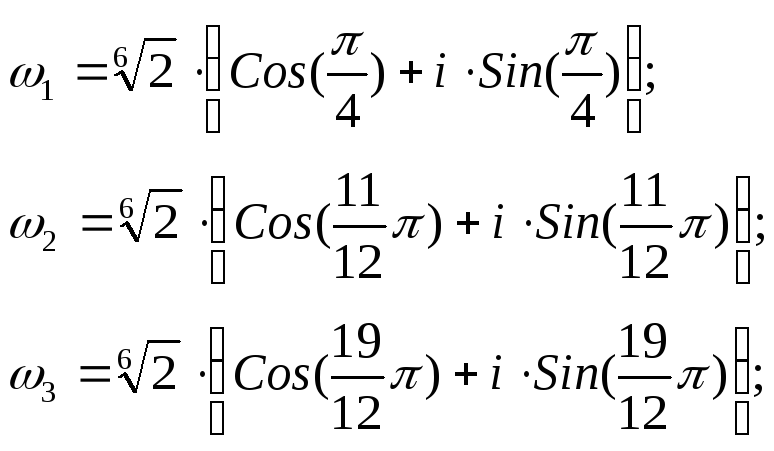
На комплексной плоскости корни распределяются равномерно по окружности.