Решить дифференциальное уравнение:

(55)

Решение. Уравнение (55) представляет собой дифференциальное уравнение 3-го порядка, в котором в явном виде отсутствует искомая функция у. Следовательно оно является уравнением вида (53). Так как у^// - это низшая производная, входящая в уравнение (55), то мы можем понизить его порядок сразу на две единицы с помощью замены: у^|| = z (x). Тогда у^/// = z^/ (x) и уравнение (55) принимает вид:

(56)

Последнее уравнение есть уравнение 1-го порядка с разделяющимися переменными. Решим его (см § 3): ;

;

.

Положим С₁ = ± С (где C₁ = const, C₁ ≠ 0), тогда

,

но так как z = y^//, после обратной замены получаем следующее дифференциальное уравнение: (57)

Уравнение (57) относится к виду (45). Решим его.

;

;

;

;

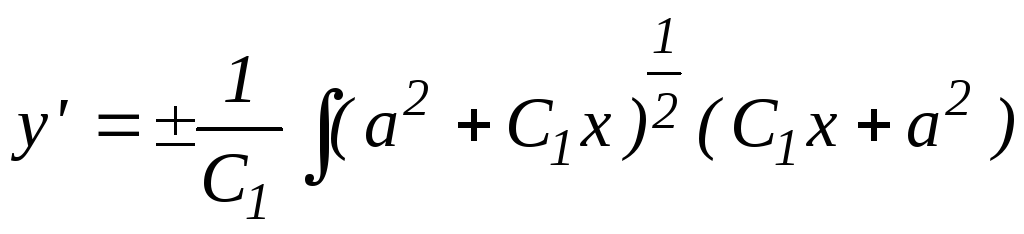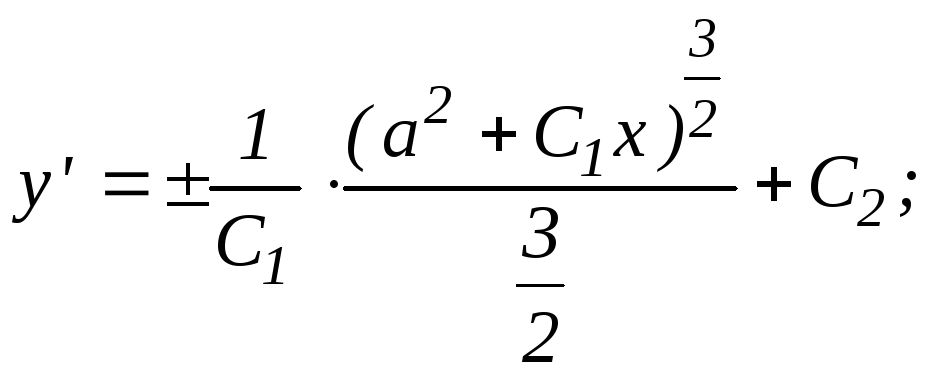
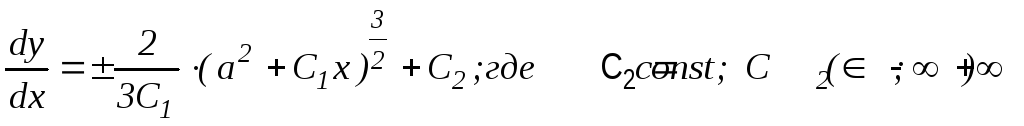
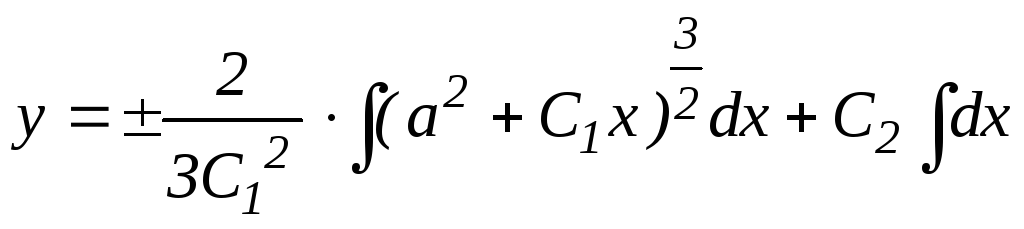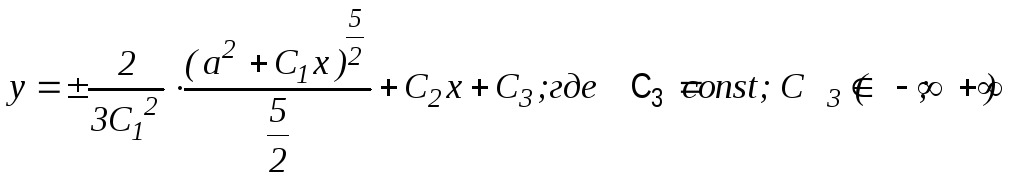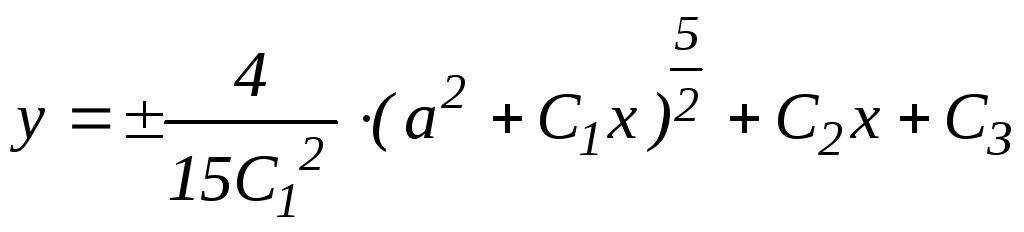. (58)

Итак, формула (58) определяет общее решение заданного уравнения (55).

Проверим, не потеряли ли мы решения, наложив ограничение z²– a² ≠ 0, т.е. z ≠ ± а.

Пусть z = ± а, т.е. у^|| = ± а. Откуда после двукратного интегрирования находим:

(59)

Непосредственной проверкой убеждаемся, что семейство функций (59) является решением заданного уравнения (55) (действительно, подставив (59) в (55) имеем тождество ), причем оно не может быть получено из общего решения (58) ни при каком наборе числовых значений произвольных С1, С2, С3.

Окончательно, совокупность всех решений уравнения (55) следующая

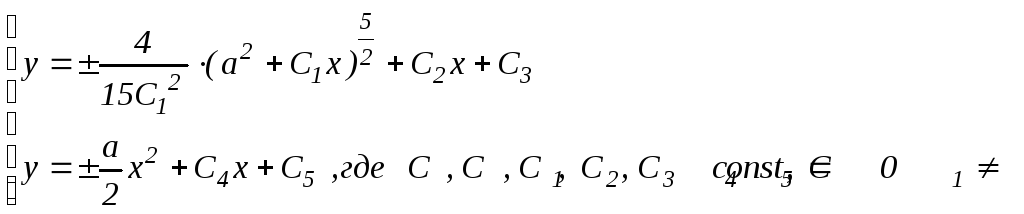
Ответ:

3. Уравнение вида: F (y, y^|, y^||,….y⁽ⁿ⁾)= 0 (60)

Отличительная особенность уравнения (60) в том, что оно явно не содержит независимую переменную х. Порядок такого дифференциального уравнения можно понизить на единицу, если положить у^/ = z ( где z = z(у) – новая искомая функция, а у – новый аргумент). В этом случае производные у^//, у^///,…находятся (согласно правилу дифференцирования сложной функции) по формулам:

(61)

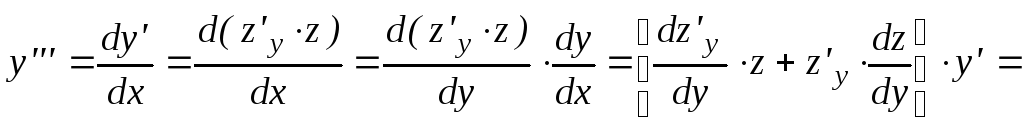
и т. д.

Пример 10.

Решить задачу Коши: 2уу^// = (у^/)² + 1 (62)

у (0) = 1

у^/ (0) = -1 (63)

Решение. Уравнение (62) есть уравнение 2-го порядка, не содержащее явно независимую переменную х, а поэтому оно относится к виду (60). Понизим порядок данного уравнения (62) на единицу, положив у^/ = z (y). Откуда .

После подстановки у^/ = z и в уравнение (62) имеем:

(64) Уравнение (64) представляет собой уравнение 1-го порядка с разделяющимися переменными. Решим его. . Пологая, что у ≠ 0, делим обе части последнего уравнения на : ;

.

Приняв С₁ = ± С (C₁ = const, C₁ ≠ 0), имеем:

.

Но, так как z = y^|, то после обратной подстановки получаем следующее дифференциальное уравнение: . Откуда . Пологая, что, получаем:;

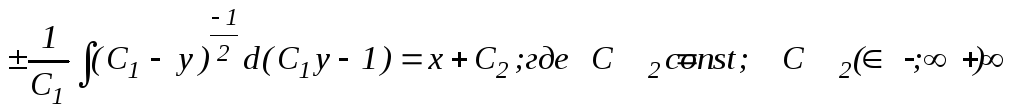
. (65)

Итак, формулой (65) определяется общее решение заданного уравнения (62). Заметим, что в процессе решения налагались ограничения у ≠ 0 и у ≠ С^-1₁. Поэтому необходимо проверить, не утрачены ли при этом решения у =0 и у =С₁^-1. Функции у= =0 и у =С₁^-1, будучи подставленными в уравнение (62), не обращают его в тождество, а значит они не являются его решениями. Следовательно, формула (65) определяет все решения данного уравнения. Найдем частное решение уравнения (62), удовлетворяющее начальным условиям (63):

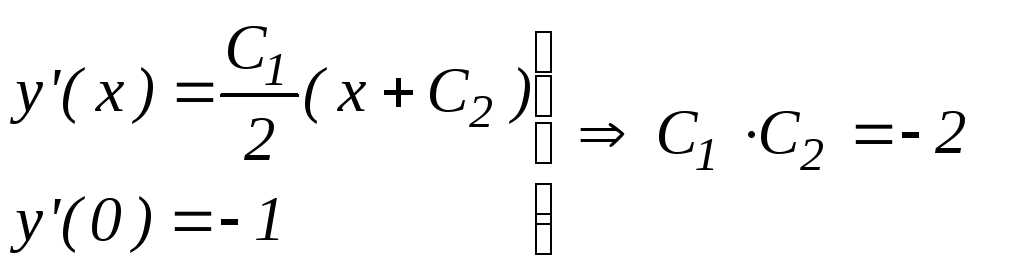
Получаем в результате систему: 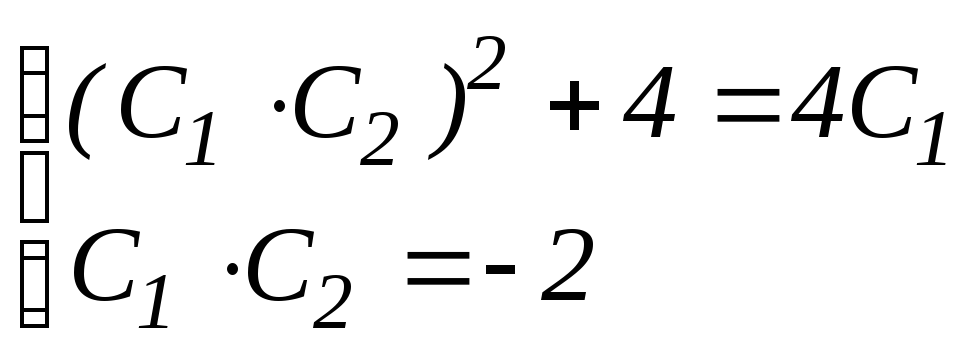, решением которой будет: С₁ = 2, С₂ = - 1 . Таким образом, искомое частное решение имеет вид:

(66)

С геометрической точки зрения функция (66) определяет интегральную кривую (параболу с вершиной в точке и осью симметрии, параллельной оси ординат), проходящую на плоскости ХОУ через точку М_о (0; 1) и имеющую в ней касательную с угловым коэффициентом k = -1 (так как k = tgφ = -1, то касательная образует с положительным направлением оси Ох угол φ = 135⁰).