Линейные дифференциальные уравнения порядка n
Линейным дифференциальным уравнением порядка n называется уравнение, в котором неизвестная функция У и её производные до порядка n входят линейно.
(67)
Если
правая часть
,
то уравнение называется однородным.
Если в уравнении (67) коэффициент
,
то оно приводится к каноническому виду
путём деления всех его членов на этот
коэффициент:
(68)
Линейные однородные уравнения
Теорема существования и единственности решения Коши для ЛОДУ принимает следующую форму:
Если
коэффициенты
- непрерывны на
то уравнение
удовлетворяет
условиям теоремы Коши для уравнения,
разрешенного относительно старшей
производной. Поэтому для любой точки
(n+1)
-
мерного
пространства
существует и притом единственное решение
ЛОДУ, определённое в некотором интервале,
содержащем точку
и удовлетворяющее начальным условиям:
.
Отметим некоторые свойства ЛОДУ.
1).
Если функции
- решения ЛОДУ, то линейная комбинация
этих решений с любыми числовыми
коэффициентами вида
так же будет решением этого уравнения.
Свойство распространяется на любое
конечное число решений уравнения.
2).
Если ЛОДУ с коэффициентами – функциями
действительного переменного
имеет комплексное решение
,
то действительная часть этого решения
– функция
и коэффициент при мнимой части – функция
каждая в отдельности так же являются
решениями ЛОДУ. Доказательство свойства
вытекает из общего свойства комплексных
чисел: сумма, разность, произведение,
частное комплексных чисел, сопряжённых
с данными, есть комплексное число,
сопряжённое с суммой, разностью,
произведением, частным исходных
комплексных чисел.
3). Всякое ЛОДУ имеет «нулевое» (тривиальное) решение.
Перед тем, как перейти к вопросам решения ЛОДУ, введём понятие линейной зависимости и независимости функций, аналогичное понятиям линейной зависимости и независимости системы векторов в линейном векторном пространстве.
Функции
назовём линейно
зависимыми
на сегменте
,если
существуют постоянные коэффициенты
такие, что для
выполняется тождественное равенство:
,
при этом не все постоянные коэффициенты
равны нулю. Если указанное тождество
выполняется лишь при условии
,
то функции называются линейно
независимыми.
Пример.
Являются
ли функции
линейно зависимыми на
?
Решение.
Составим линейную комбинацию из данных
функций:
.
По следствию из основной теоремы алгебры,
у многочлена степени n
с действительными коэффициентами может
быть только n
корней, поэтому тождественное равенство
нулю для линейной комбинации для любого
х из указанного промежутка возможно
только при условии
.
Следовательно, предложенная совокупность
функций является линейно независимой.
Однако, решить вопрос о линейной зависимости или независимости функций на основании лишь данного выше определения возможно лишь в очень простых случаях. В общем случае этот вопрос решается следующей теоремой:
Теорема.
Если непрерывные и (n-1)
раз дифференцируемые на некотором
интервале функции
- линейно зависимы, то на этом же интервале
определитель
Вронского
(польский математик, 1775 – 1853 г.),
составленный для этих функций, будет
тождественно равен нулю:
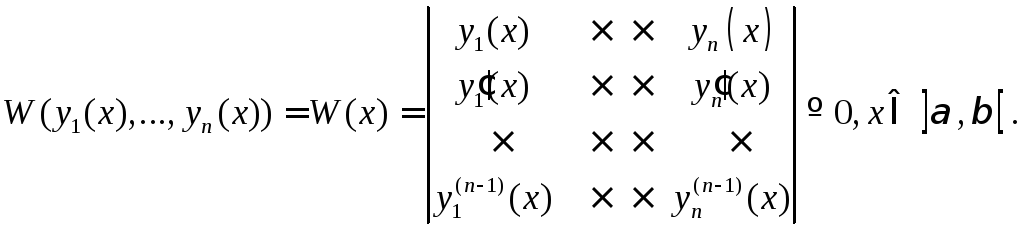(69)
Доказательство. Составим равную нулю линейную комбинацию из n линейно зависимых функций и продифференцируем её (n-1) раз:
(не
все коэффициенты, входящие в линейную
комбинацию, равны нулю).
Для
любого фиксированного
написанная выше система уравнений
относительно коэффициентов
является системой линейных однородных
алгебраических уравнений, имеющей
ненулевое решение. А это может быть лишь
в случае, если определитель, составленный
из коэффициентов при неизвестных (а это
– определитель Вронского) равен нулю.
Теорема доказана.
Замечание.
Если данные функции – линейно независимы
на промежутке
,
то составленный из них определитель
Вронского может принимать нулевое
значение лишь в конечном числе точек
этого промежутка.
Отметим
важное свойство решений ЛОДУ. Если
функции
- линейно независимы на промежутке
,
и каждая из них одновременно является
решением ЛОДУ, удовлетворяющего условиям
теоремы Коши на этом промежутке, то
определитель Вронского для этих функций
не обращается в нуль ни в одной точке
этого промежутка:
.
(Свойство приводим без доказательства).
Теорема.
Общим решением ЛОДУ порядка n,
удовлетворяющего условиям теоремы
Коши, является линейная комбинация из
n
его линейно независимых на
частных решений
,
взятых с произвольными постоянными
коэффициентами
:
.
(70)
Доказательство.
Утверждение, что линейная комбинация
(70) – решение ЛОДУ, вытекает из свойства
1) ЛОДУ (см. выше). Решение (70) будет общим,
если оно содержит в себе все частные
решения. Зададимся произвольными
начальными условиями:
.
Так как ЛОДУ удовлетворяет условиям
теоремы Коши, то выбранным начальным
условиям будет соответствовать
единственное частное решение, которое
может быть получено следующим образом.
Для выбранных начальных условий можно
записать:
(71)
Система уравнений (71) относительно произвольных констант – линейная алгебраическая неоднородная. Её определитель совпадает с определителем Вронского, который отличен от нуля в силу отмеченного ранее свойства решений ЛОДУ. Следовательно, ранг системы равен числу неизвестных и решение у системы (71) – единственное, т. е. набор констант = единственный для любого набора начальных условий задачи Коши.
Следствие.
Максимальное число линейно независимых
частных решений ЛОДУ порядка n,
составляющих его общее решение, равно
порядку уравнения, т. е. равно числу n.
Легко показать, что если составить общее
решение из (n+1)-
ого частного решения то ранг системы,
аналогичной системе (71), будет равен n
и «лишний» (n+1)
столбец войдёт в решение только для n
констант
.
Любые n линейно независимые решения ЛОДУ порядка n составляют его фундаментальную систему решений.
Пример.
Какие
из частных решений
могут составить фундаментальную систему
решений ЛОДУ
?
Решение. ЛОДУ второго порядка, поэтому
его фундаментальная система решений
включает в себя только два линейно
независимых частных решения. Составим
определитель Вронс-
кого для предложенных частных решений.
Следовательно,
частные решения
образуют фундаментальную систему
решений на любом интервале числовой
оси.
Пример.
Дано
ЛОДУ:
Его частными решениями являются функции:
Образуют ли они фундаментальную систему
решений?
Частные
решения образуют фундаментальную
систему решений на любом интервале, не
содержащем точку Х=0.
Методы решения ЛОДУ.
Общих методов решения ЛОДУ в полном виде с переменными коэффициентами – произвольными функциями даже для уравнений второго порядка не существует. Существует лишь метод решения ЛОДУ второго порядка для случая, когда одно нетривиальное частное его решение подобрано или определено из каких – либо иных соображений. Существует так же метод понижения порядка ЛОДУ на единицу, если известно одно его частное решение. Два известных частных решения позволят понизить порядок ЛОДУ соответственно на две единицы и т. д.
Нахождение общего решения ЛОДУ второго порядка с использованием
формулы Лиувиля – Остроградского.
Пусть дано ЛОДУ второго порядка, записанного в канонической форме и известно одно его частное решение:
-
известное частное решение.
Введём
новую неизвестную функцию
,
положив
-решение ЛОДУ.
Подставим предполагаемое решение в данное ЛОДУ и проведём некоторые преобразования:
Вторая скобка в последнем равенстве равна нулю, так как представляет из себя результат подстановки в ЛОДУ его же частного решения. Поэтому будем иметь:
(72)
Порядок
уравнения (72) может быть понижен на
единицу, так как в его составе в явном
виде отсутствует неизвестная функция
.
Полагаем
тогда
.
Здесь
- новая неизвестная функция. В новой
переменной уравнение (72) примет вид:
- уравнение первого порядка с разделяющимися
переменными. Решаем
его:
Решение исходного ЛОДУ примет вид:
Здесь второе частное решение найдено по формуле Лиувиля – Остроградского:
(73)
Пример.
Дано ЛОДУ второго порядка и известно одно его частное решение. Найти общее решение уравнения.
-
известное частное решение.
Для нахождения второго частного решения используем формулу Лиувиля - Остроградского:
Общее
решение имеет вид:
Метод понижения порядка.
Дано ЛОДУ второго порядка и известно одно его частное решение:
-
известное частное решение.
Понизим порядок уравнения на единицу при помощи следующей подстановки:
,
где
-
новая неизвестная функция. Продифференцируем
выражение дважды:
После подстановки в ЛОДУ и некоторых преобразований будем иметь:
Первая скобка в последнем выражении равна нулю (как результат подстановки частного решения в само уравнение), поэтому в окончательном виде уравнение в новой переменной получит выражение:
(74)
Уравнение (74) – линейное, неоднородное, первого порядка. Его можно решить методом вариации произвольной постоянной Лагранжа или методом Бернулли.
Пример. Решить предыдущий пример методом понижения порядка.
Подстановка:
В новой переменной заданное уравнение примет вид:
Его
решение:
Общее решение ЛОДУ следующее:
Следует упомянуть, что профессором Кислым А. А. разработан метод решения ЛОДУ с переменными коэффициентами второго, третьего и четвёртого порядков для целого ряда видов переменных коэффициентов. При этом производные неизвестной функции по времени заменяются её производными по новой переменной, что позволяет превратить ЛОДУ с переменными коэффициентами в ЛОДУ с постоянными коэффициентами, общее решение которого всегда может быть надено.