Предел функции двух переменных.

Говорят, что последовательность точек с координатами стремится к точке с координатами , если последовательность расстояний точек от точки стремится к нулю при . Таким образом, последовательность точек стремится к, если

т. е. если стремится к , а -- к .

Говорят, что есть предел функции , где (х, у) стремится к , если для каждой последовательности точек , отличных от и стремящихся к , последовательность стремится к при . Это записывается следующим образом:

Частные производные первого порядка

Рассмотрим функцию . Пусть независимая переменная у приняла постоянное значение , а переменная изменяется. Тогда из функции двух переменных получим функцию одной независимой переменной .

Ее графиком является линия пересечения поверхности и плоскости (рис 10).

Поскольку является функцией одной переменной, ее производная в точке вычисляется по формуле

Рис. 10.

Эта производная называется частной производной от функции двух переменных в точке .

Обозначим через приращение переменной х; введем также обозначение

Приращение называют частным приращением функции z по переменной х.

Аналогично, если переменная у получает приращение , а х остается постоянной, то частное приращение функции z по переменной у имеет следующий вид:

Если существует предел

то этот предел называется частной производной первого порядка или первой частной производной по переменной х; она обозначается следующими символами:

.

Аналогично определяется первая частная производная по переменной у

как предел отношения

.

Пример 1. Найти первые частные производные функции

.

Решение. Чтобы найти частную производную по , принимаем у за постоянную и находим производную по х:

(Производную приняли равной нулю, поскольку у считаем постоянным числом. В первом слагаемом постоянную вынесли за знак производной.)

Чтобы найти частную производную по у, принимаем х за постоянную и находим производную по у.

Пример 2. Найти первые частные производные функции

.

Решение. Чтобы найти частную производную по , принимаем у за постоянную и находим производную по х:

Чтобы найти частную производную по у, принимаем за постоянную и находим производную по у:

.

Градиент функции. Производная по направлению вектора.

Градиентом функции называется вектор, проекциями которого на оси координат являются частные производные данной функции:

.

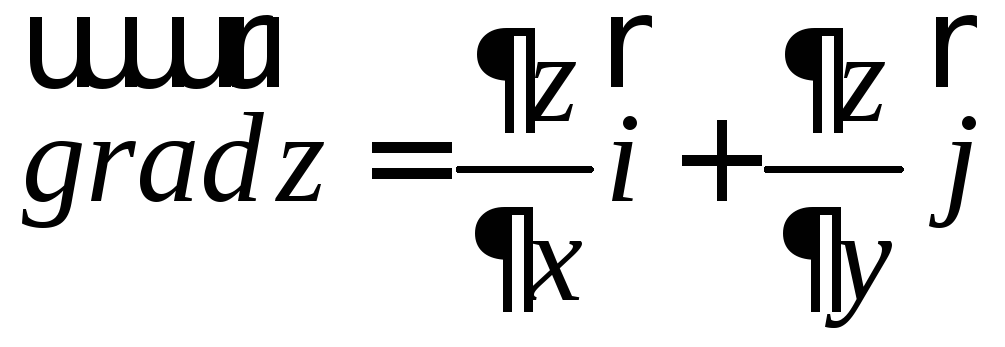Производной функции в данном направлении называется

.

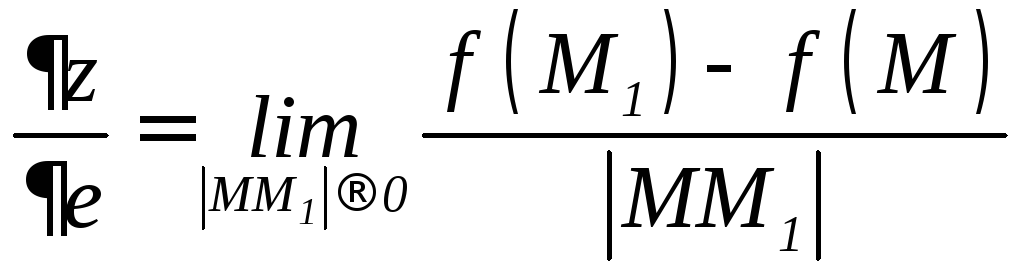Если функция дифференцируемая, то производную в данном направлению можно найти по формуле

,

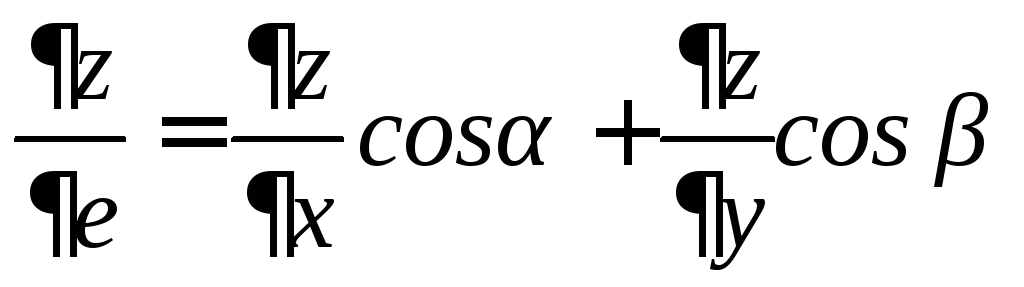где - направляющие косинусы вектора .

● Пример 4. Дана функция , точка и вектор . Найти: 1) в точке ; 2) производную в точке по направлению вектора .

Решение. 1) Найдем частные производные данной функции:

; .

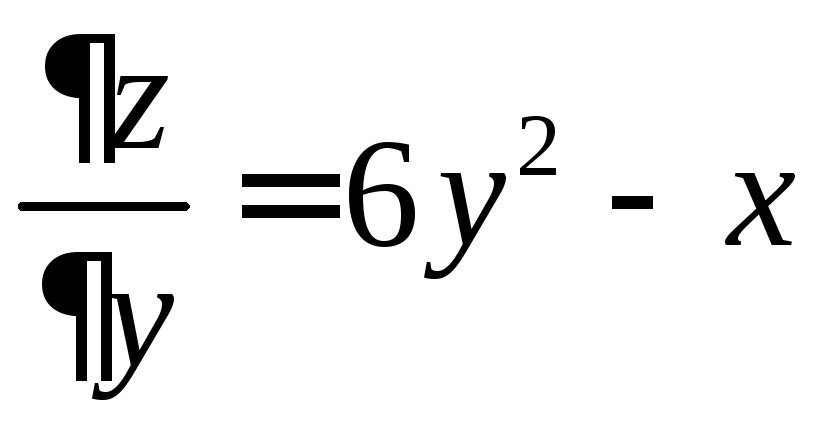Градиент данной функции в произвольной точке равен

.

Определим градиент в точке

.

2) Найдем производную функции в точке по направлению вектора.

Частные производные функции в точке равны

; .

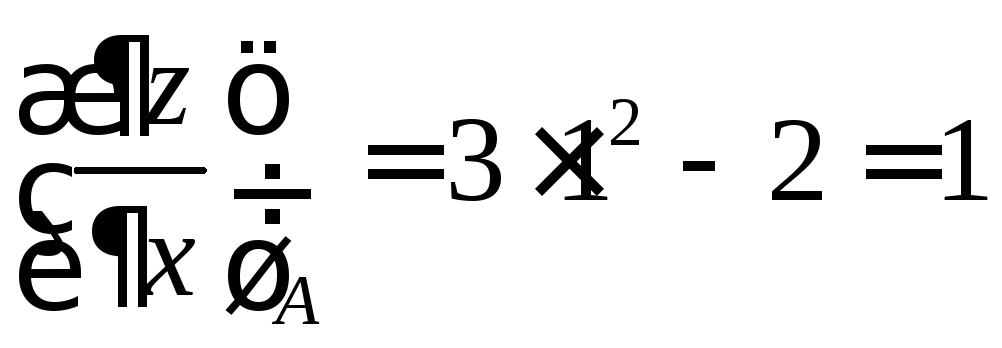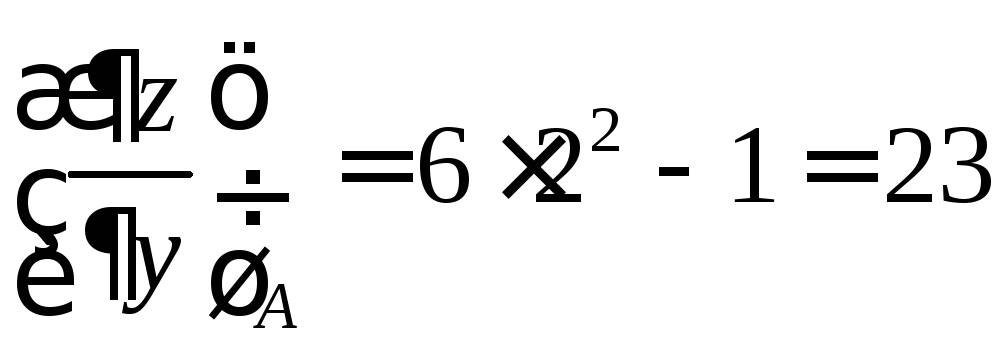Определим направляющие косинусы вектора

;

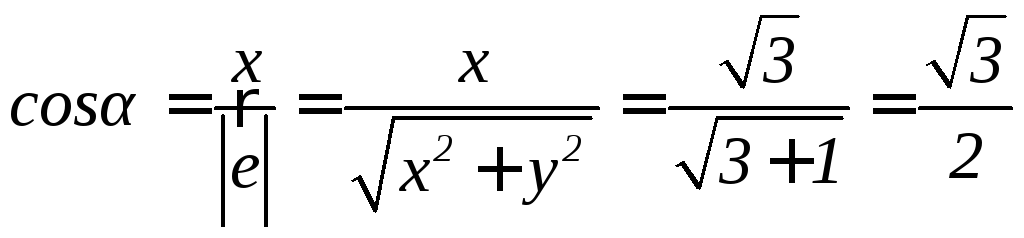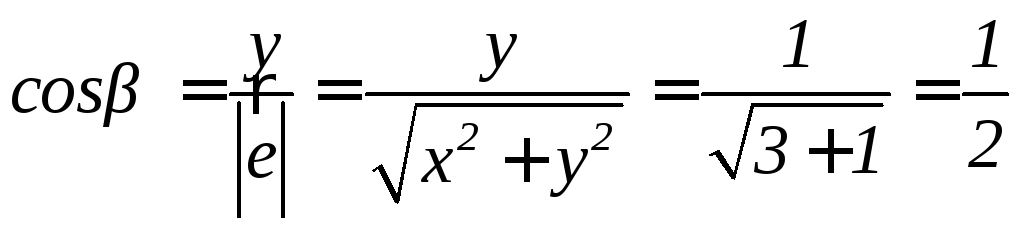
Отсюда, искомая производная

.●

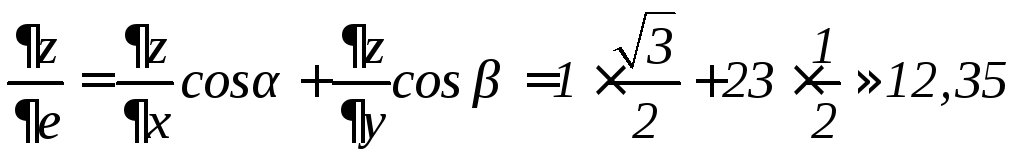Вопросы для самоконтроля

1. Понятие о функции нескольких переменных.

2. Полное и частное приращение функции.

3. Частные производные функций нескольких переменных.

4. Полный дифференциал.

5. Касательная плоскость и нормаль к поверхности.

6. Частные производные и дифференциалы высших порядков.

7. Необходимый признак экстремума функций двух переменных.

8. Нахождение функции на основании экспериментальных данных по методу наименьших квадратов.