Вопросы для самоконтроля
Частные и общие решения дифференциального уравнения 1-го порядка.
Дифференциальные уравнения с разделяющимися переменными.
Однородные уравнения.
Линейные уравнения.
Уравнения Бернулли.
Частные и общие решения дифференциального уравнения 2-го порядка.
Дифференциальные уравнения вида
.Дифференциальные уравнения вида
.Дифференциальные уравнения вида
;
.Дифференциальные уравнения вида
;
.Основная теорема об общем решении линейного однородного уравнения 2-го порядка.
В каком случае
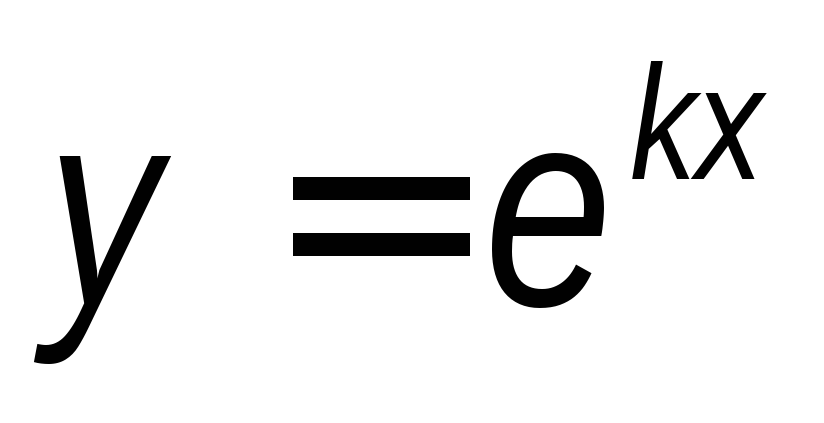является решением линейного однородного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами.Вид общего решения линейного дифференциального уравнения второго порядка в случае, если корни характеристического уравнения действительные и различные.
Вид общего решения линейного однородного дифференциального уравнения 2-го порядка, если корни характеристического уравнения кратные.
Вид общего решения линейного однородного дифференциального уравнения 2-го порядка, если корни характеристического уравнения комплексные.
Теорема об общем решении линейного неоднородного дифференциального уравнения 2-го порядка.
Метод Лагранжа решения неоднородного линейного дифференциального уравнения 2-го порядка.
Дифференциальные уравнения малых колебаний механических систем.
Литература
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2-х томах, том 1, изд. «Наука», М.,1972 г., 456 стр. с илл.
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2-х томах, том 2, изд. «Наука», М.,1972 г., 456 стр. с илл.
Слободская В.А. Краткий курс высшей математики. Изд. 2-е, переработ. и доп. Учеб. пособие для втузов. М., «Высшая школа», 1969. 544стр. с илл.
Письменный Д.Т. конспект лекций по высшей математике: полный курс.-4-е изд.-М.: Айрис-пресс, 2006.-608 с.: ил. – (высшее образование).