Конспект лекции по ТЭС

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

по времени одной, достаточно длинной, реализации: X (t)

по времени одной, достаточно длинной, реализации: X (t)

.pdf

Скачиваний:

112

Добавлен:

10.06.2015

Размер:

1.85 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 155 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

ЛЕКЦИЯ 11

Вероятностные характеристики случайных процессов.

Случайные величины и их вероятностные характеристики: интегральная функция распределения, плотность вероятности и их свойства. Совместное распределение вероятностей двух случайных величин. Условная плотность вероятности. Независимость совокупности случайных величин. Функциональные преобразования случайных величин. Основные числовые характеристики: мода, медиана, математическое ожидание, дисперсия, коэффициент корреляции. Нормальный или гауссовский закон распределения случайных величин.

Теория вероятностей – это наука, изучающая закономерности в случайных событиях или явлениях. Числовой мерой достоверности случайного события является вероятность.

Вероятность появления некоторого события A в опыте (испытании, измерении) равна

P( A) lim	N A	,	(76)

N N

где N A – число опытов, в которых событие A произошло, N – общее число опытов.

Вероятность события может принимать значения от 0 (невозможное событие) до 1 (достоверное событие).

Случайные величины Случайная величина (СВ) – это некоторая числовая величина, принимающая, в

зависимости от случая, свои значения с заданными вероятностями. Если вероятность СВ не равна единице, то её значение в конкретном опыте достоверно предсказать невозможно.

Случайные величины могут быть дискретными и непрерывными. Дискретные СВ являются частным случаем непрерывной СВ, поэтому, в дальнейшем, ограничимся описанием свойств и характеристик непрерывных СВ.

Случайные величины или события обычно обозначают большими буквами (прописью), а конкретное её значение или реализацию случайной величины в опыте обозначают строчными буквами. Например, X – случайная величина, x – значение этой случайной величины.

Интегральная функция распределения и плотность вероятности

Важными характеристиками случайных величин являются интегральная функция распределения (ИФР) и плотность вероятности (ПВ). ИФР и ПВ случайной величины X

– это функции от неслучайного аргумента, которые равны

				x		( x ) – ИФР,
	FX (x) P( X x) wX (t)dt					( x ) – ИФР,		(77)

wX	(x) lim	P(x X x x)			dFX (x)		( x ) – ПВ.	(78)
			x			x

	x 0

Если при написании ИФР или ПВ индекс, обозначающий случайную величину к которой они принадлежат, не указан, то принадлежность их к случайной величине определяют по обозначению аргумента.

Свойства интегральной функции распределения:

1) 0 FX (x) 1 ;

2) FX ( ) 0, FX ( ) 1 ;

3) FX (x1 ) FX (x2 ) , если x1 x2 .

Свойства плотности вероятности:

1)wX (x) 0 ;

2)вероятность того, что СВ примет своё значение внутри заданного интервала, равна

x2
P(x1 X x2 ) wX (x)dx ;	(79)
x1

3) условие нормировки ПВ: wX (x)dx 1 (вероятность достоверного события);


4) плотность вероятности дискретной СВ X xk , k 1, 2,..., n с	pk P( X xk ) равна
n
wX (x) pk (x xk ) .	(80)
k 1

Совместное распределение вероятностей двух случайных величин

Обобщением распределения одной СВ является совместное распределение двух и более СВ. Для их полного описания необходимо задать многомерную ИФР или многомерную ПВ.

Рассмотрим совместное распределение двух СВ X и Y . Их совместная ПВ и ИФР по определению равны

			x		y
FX ,Y (x, y) P( X x,Y y)					wX ,Y (t, v)dtdv ,		(81)

wX ,Y (x, y) lim		P(x X x		x, y Y y y)		.	(82)

			x		y
x 0
y 0							X ,

Если известно распределение двух СВ, то распределение одной из них, например
можно найти по формулам
x
FX (x) FX ,Y (x, )	wX ,Y (t, v)dtdv ,				wX (x) wX ,Y (x, y)dy .		(83)

Условная плотность вероятности

Если распределение вероятностей одной случайной величины в опыте зависит от того, какое значение приняла в опыте другая случайная величина, то такие СВ являются зависимыми. Для выражения вероятностной зависимости СВ друг от друга в теории вероятностей вводятся условные плотности вероятности.

Совместную плотность вероятности двух СВ можно найти через условные плотности вероятности wY |X ( y | x) и wX |Y (x | y) по известной формуле Байеса

wX ,Y (x, y) wX (x)wY \| X ( y \| x) wY ( y)wX \|Y (x \| y) .						(84)
Откуда легко выразить условную плотность вероятности Y :
wY \|X ( y \| x)	wX ,Y	(x, y)	wX ,Y	(x, y)
					.	(85)
	wX				.	(85)
	wX	(x)	wX ,Y	(x, y)dy
			wX ,Y	(x, y)dy

Независимость совокупности случайных величин
Случайные величины X1, X 2 ,..., X n		являются независимыми, если
			n
wX1 , X 2 ,..., X n (x1, x2 ,..., xn ) wX k (xk ) .						(86)
			k 1

Если это условие не выполняется, то X1, X 2 ,..., X n являются зависимыми СВ.

Функциональные преобразования случайных величин

Довольно часто приходится решать задачи, в которых требуется найти распределение случайной величины, полученной в результате функционального преобразования случайных величин с известным распределением.

Рассмотрим две типичные задачи функционального преобразования.
Случай 1. ИФР или плотность вероятности X известны, а Y получена из X	путём
функционального преобразования
y f (x) .
Используя определение ИФР, находим
FY ( y) P(Y y) P( f ( X ) y) P( X fx( 1) ( y)) FX fx( 1) ( y) ,	(87)

где fx( 1) ( y) – обратная функция по отношению к f (x) .

Тогда

wY ( y)

FY ( y)

FX fx( 1) ( y) wX

fx( 1) ( y)

fx( 1) ( y) wX

fx( 1) ( y)

(88)

Учитывая, что wY ( y) 0 , получим

wY ( y) wX fx( 1) ( y)

(89)

, т.е.

Если обратная функция x

fx( 1) ( y) неоднозначная

при заданном

существует

несколько значений x :

fx( 1) ( y) x1 fx( 1) ( y), x2

fx( 1) ( y),..., xn

fx( 1) ( y) , то

( 1)

( y)

FY ( y) P X x1 X x2 ... X xk ... FX

(90)

fxk

k 1

( 1)

dxk

wY ( y) wX fxk

( y)

(91)

k 1

Пример. Значения X и Y связаны зависимостью y x2 .

FY ( y) P(Y y) P( X 2 y) P X

(92)

wY ( y)

FY ( y) wX

y 0 .

(93)

Случай 2. СВ Y связана с двумя СВ X1

и X 2

функциональным преобразованием

y f (x1, x2 ) .

Аналогично случаю 1, находим

P X1 x1, X

(x1, y)

FY ( y) P(Y y) P f ( X1, X 2 ) y

( 1)

2 fx2

x1 ( ; )

( 1)

(x1, y) | X1

( 1)

(x1, y) | x1 dx1 .

P X1 x1 P X 2 fx2

wX1 (x1 )FX 2 | X1 fx2

x1 ( ; )

Плотность вероятности Y найдём как производную от FY ( y)

по y :

( 1)

wY ( y)

FY ( y) wX1 (x1 )wX 2 | X1 fx2

(x1, y) | x1

fx2

(x1, y)dx1 .

С учётом неотрицательности ПВ, получим

( 1)

wY ( y)

wX1 , X 2 x1, fx2

( y, x1 )

fx2

( y, x1 )

dx1

Пример 1. Дано y x x . Тогда f ( 1) (x , y) x

y x ,

f ( 1)

(x , y) 1

wY ( y)

wX1 , X 2 (x, y x)dx .

Если X1 и X 2

независимые СВ, то ПВ Y будет равна их свёртке

wY ( y) wX1 (x)wX 2 ( y x)dx .

Пример 2. Дано y x x . Тогда

f ( 1)

(x , y) x

y / x ,

( 1) (x , y) 1/ x

wY ( y)

wX1 , X 2 x,

dx .

(94)

(95)

(96)

(97)

Основные числовые характеристики случайных величин Мода – значение случайной величины, при которой плотность вероятности достигает

своего максимума.

Медиана – значение случайной величины, в которой площадь, ограниченная кривой плотности вероятности, делится пополам.

Математическое ожидание или статистическое среднее

M X
M X		X	mX	x wX (x)dx .	(98)
Дисперсия
Дисперсия

	X mX 2
D X M X 2	X mX 2			2X (x mX )2 wX (x)dx ,	(99)

	D X M X 2 mX2 ,				(100)

где X – среднеквадратическое отклонение случайной величины, которое определяет меру


разброса случайной величины около своего среднего значения,				X X mX –
центрированная случайная величина.
Коэффициент корреляции

	M{X Y}	1
X ,Y			(x mX ) ( y mY )wX ,Y (x, y)dxdy .	(101)
		X Y
	X Y

Коэффициент корреляции является одним из показателей линейной зависимости СВ.

Свойства коэффициента корреляции: 1) 1 X ,Y 1;

2) если X ,Y	0 , то X и Y – некоррелированные СВ;
3) если X ,Y	1 , то X и Y – линейно-зависимые СВ.
Если Y aX b , то X ,Y sign(a) . При этом wX ,Y (x, y) wX (x)( y ax b) .
Если СВ статистически независимые, то коэффициент корреляции равен X ,Y		0 , т.е.

из условия независимости СВ следует их некоррелированность. Наоборот не всегда справедливо.

Нормальный или гауссовский закон

Если X – нормальная (гауссовская) СВ с M X mX и D X 2X , то

		1			( x mX )2
	wX (x)	1		e	2 2X	.	(102)

			22X
Свойства:			22X
Свойства:
1)	при X 0 wX (x) (x mX ) , а при X					wX (x) 0 ;
2)	закон 3 : P mX 3X X mX	3X P \| X mX					\| 3X 0, 997 ;
3)	если две нормальные СВ некоррелированные, то они также независимые.

Центральная предельная теорема теории вероятностей доказывает, что сумма

достаточно большого числа независимых	СВ есть СВ, распределённая	по нормальному
(гауссовскому) закону. В частном случае, алгебраическая сумма		Y X1 X 2 двух
независимых нормальных СВ X1 и X 2 будет также распределена по нормальному закону с
M Y M X1 M X 2	и D Y D X1 D X 2 .	(103)

ЛЕКЦИЯ 12

С л у ч а й н ы е процессы. Основные характеристики случайных процессов: математическое ожидание и дисперсия случайных процессов. Корреляционная функция и коэффициент корреляции случайного процесса и их свойства. Взаимная корреляционная функция случайных процессов.

Случайные процессы

Случайный процесс – это случайная функция от неслучайной переменной времени t .

Он образуется множеством	детерминированных	(неслучайных) функций	времени xi (t)
( i 0,1,..., ), которые называют реализациями случайного процесса X (t) .			Значение СП в
некоторый момент времени	является случайной	величиной и называется	сечением СП.

Например, если X (t) – случайный процесс, то X i X (ti ) – сечение случайного процесса в момент времени ti .

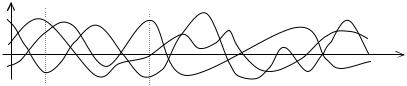
Для полного описания случайного процесса необходимо задать совместное

распределение всех его сечений.		и X1 обозначают сечения СП X (t) в моменты времени t0 и
На следующем рисунке X0		и X1 обозначают сечения СП X (t) в моменты времени t0 и
t1 , а функции x0 (t) ,	x1(t) и x2 (t)	– его выборочные реализации.
X (t)	X 0	X1
x0 (t)
x1 (t)
x2 (t)		t
	t0	t1
	Рис. 31. Реализации случайного процесса и его сечения.

Случайные сигналы, к которым относятся помехи, шумы и другие сигналы случайного происхождения, в теории связи рассматриваются в виде случайных процессов.

Основные характеристики случайных процессов

Для случайных процессов, как и для случайных величин, можно найти математическое ожидание и дисперсию:

(x, t)dx ,

(104)

X (t)

(t) X (t)

x w

(t))2 w

X 2

X (t)

(t)

X (t) m

(t)

(x m

(x, t)dx M

(t)

(t) ,

(105)

X (t) X (t) mX (t)

– центрированный СП, mX (t) – регулярная составляющая СП.

Корреляционная функция

mX (t1 ) x2 mX (t2 ) wX (x1 , x2 , t1 , t2 )dx1dx2 .

BX (t1 , t2 ) X (t1 ) X (t2 )

(106)

BX (t1,t2 ) X (t1 ) X (t2 ) X (t2 ) X (t1 ) BX (t2 ,t1 ) ,

BX (t, t ) BX (t, t ) .

(107)

Коэффициент корреляции

BX (t1,t2 )

X (t1

,t1 )

(108)

X (t1 ) X (t2 )

Свойства коэффициента корреляции:

1)1 X (t1, t2 ) 1;

2)X (t1, t2 ) 0 , если сечения X (t1 ) и X (t2 ) некоррелированные;

3)X (t1, t2 ) 1 , если сечения X (t1 ) и X (t2 ) линейно-зависимые.

Взаимная корреляционная функция различных случайных процессов X (t) и Y (t)


BX ,Y (t1,t2 ) X (t1 )Y (t2 ) M X (t1 )Y (t2 )						x mX (t1 ) y mY (t2 ) wX ,Y (x, y, t1,t2 )dxdy . (109)

ЛЕКЦИЯ 13

Стационарные и нестационарные случайные процессы. Корреляционная функция и коэффициент корреляции стационарного случайного процесса и их свойства. Интервал корреляции. Эргодические случайные процессы. Гауссовские и марковские случайные процессы.

Стационарные и нестационарные случайные процессы

Случайные процессы можно разделить на два класса – стационарные и нестационарные.

Строго стационарными или стационарными в узком смысле называют такие случайные процессы, плотность вероятности или интегральная функция распределения которых не зависит от произвольного временного сдвига. Если X (t) – строго стационарный

случайный процесс, то
wX (x1, x2 ,..., xn , t1, t2 ,..., tn ) wX (x1, x2 ,..., xn , t1 , t2 ,..., tn )	при любом .	(110)

Одномерная плотность вероятности стационарного СП wX (x, t) wX (x, t ) wX (x) – не зависит от времени, а двумерная плотность вероятности wX (x1, x2 , t1, t2 ) w(x1, x2 , ) – зависит от разности моментов времени t2 t1 .

Стационарные в широком смысле случайные процессы характеризуются тем, что их математическое ожидание и дисперсия не зависят от времени, а корреляционная функция

зависит только от разности моментов времени:

Нестационарные

X (t)

const ;

случайные процессы

X (t)

Стационарные

M X 2 (t) mX2 2X

D X (t)

X (t) mX (t) 2

const ;

в широком смысле

Строго

стационар-

ные

BX (t,t ) X (t) X (t ) BX ( ) .

Строго стационарные СП стационарны и в широком смысле. Но наоборот не всегда

справедливо.

Свойства корреляционной функции стационарного СП:

BX ( ) BX ( ) – чётная функция от ;

BX (0) 2X

– средняя мощность центрированного СП X (t) ;

| B ( ) | B

(0) 2 .

Коэффициент корреляции стационарного СП:

X ( ) B

( ) / 2X , причём

X ()

1 .

Для чисто случайного процесса

X ()

0 при .

Интервал корреляции (радиус корреляции). Интервал кор , для которого выполняется

одно из условий BX ( ) 0

или X ( ) 0 при кор , называют интервалом или радиусом

корреляции СП. Сечения СП, отстоящие друг от друга на

кор , можно считать

некоррелированными.

Если непосредственно по форме корреляционной функции не удаётся найти кор , то для его определения можно использовать метод равновеликого прямоугольника:


Sпрямоуг.		BX (0) кор			BX ()	d ,
				0
	1
кор	1		\| BX ( ) \| d \| X ( ) \| d .				(111)
кор	BX (0)		\| BX ( ) \| d \| X ( ) \| d .				(111)
	BX (0)		0	0

BX ( )

BX (0)

0 кор

Рис. 32. Определение интервала корреляции методом равновеликого прямоугольника.

Для большого числа практических задач корреляционная функция является достаточно полной характеристикой стационарного случайного процесса. Раздел теории, который изучает свойства случайных процессов, определяемых моментами первых двух порядков, называют корреляционной теорией. В корреляционной теории не рассматриваются многомерные распределения, поэтому в рамках этой теории стационарны все случайные процессы, у которых среднее значение и дисперсия не зависят от времени, а корреляционная функция зависит лишь от разности моментов времени.

Для полного описания стационарного в широком смысле случайного процесса достаточно задать математическое ожидание и корреляционную функцию.

Эргодические случайные процессы Эргодические случайные процессы – это процессы, для которых усреднение по

множеству его реализаций (статистическое усреднение) совпадает с результатом усреднения

Необходимым условием эргодичности случайного процесса является его стационарность.

Основные характеристики эргодического СП находятся следующим образом:

T / 2

x(t) lim

x(t)dt

– постоянная составляющая x(t) ,

T T

T / 2

2 dt

(x(t) m

lim

x(t) m

– средняя мощность

переменной

T T

T / 2

составляющей x (t) x(t) x(t) ,

T / 2

() x(t) x(t ) lim

x(t)x(t )dt .

(112)

T T

T / 2

Усреднение по времени сделать значительно легче, чем выполнять усреднение по множеству реализаций, поскольку для его осуществления достаточно одной реализации случайного процесса.

Нормальные или гауссовские случайные процессы

Для нормального или гауссовского случайного процесса совместная плотность вероятности различных его сечений равна

(x , x ,..., x , t , t

,...,t

)

exp

(x m

)T A 1(x m

)

(113)

n 1

где

2 n

– вектор сечений СП в моменты времени (t , t

,..., t

x (x , x ,..., x )T

) ,

(mX ,1, mX ,2 ,..., mX ,n )T – вектор математических ожиданий этих сечений,

r1,1

r1,2

...

r1,n

r2,1

r2,2

...

r2,n

A (x mX )(x mX )

– корреляционная матрица

(симметричная),

...

n,1

n,2

n,n

элементы которой равны ri , j

(ti , t j ) .

Свойство 1: гауссовский

случайный процесс полностью

определяется

своим

математическим ожиданием и корреляционной функцией.

Свойство 2: если сечения гауссовского СП попарно некоррелированные, то они также

независимые, т.к. в этом случае A diag(2X ,k ) и

w(x1, x2 ,..., xn ,t1,t2 ,...,tn ) wX (xk ,tk ) ,

(114)

k 1

( xk mX ,k )2

где

wX (xk , tk )

... wX (x1,..., xk ,..., xn , t1,..., tk ,..., tn ) dxi

2 2X ,k

(115)

i 1

2X ,k

i k

– одномерная плотность вероятности сечения СП в момент времени tk .

Стационарные гауссовские случайные процессы

Математическое ожидание стационарного гауссовского СП не зависит от времени, а его корреляционная функция зависит от разности моментов времени. Поэтому

mX mX (1,1,...,1)T , ri , j BX (ti t j ) , rk ,k 2X ,

а корреляционная матрица A является симметричной и тёплицевой матрицей.

Следствие: стационарные в широком смысле гауссовские СП являются также строго

стационарными.
Если сечения гауссовского СП попарно некоррелированные, то A 2X In	и
n
w(x1, x2 ,..., xn ) wX (xk ) wX (x) n .	(116)
k 1

Марковские случайные процессы

Марковский случайный процесс – это СП без последействия, т.е. его условная (переходная) плотность вероятности зависит только от предыдущего состояния, в котором он находился ранее:

w(x

| x

k 1

, x

k 2

,...,t

k 1

k 2

,...) w(x

| x

k 1

, t

k 1

)

w(xk , xk 1 ,tk ,tk 1 )

(117)

w(xk 1

,tk 1 )

w(xk , xk 1,tk ,tk 1 )dxk

Марковский СП полностью описывается двумерной ПВ w(xk , xk 1, tk , tk 1) . Совместная плотность вероятности различных сечений марковского СП равна

wX (xk , xk 1,..., x0 , tk ,tk 1,...,t0 ) w(x0 ,t0 )w(x1, t1 \| x0 ,t0 )w(x2 ,t2	k	\| xi 1,ti 1 ) .(118)
	\| x1,t1 )... w(x0 ,t0 ) w(xi ,ti	\| xi 1,ti 1 ) .(118)
	i 1

Для стационарного или однородного марковского СП условная плотность вероятности зависит только от разности tk tk 1 :

w(xk , tk | xk 1, tk 1 ) w(xk | xk 1, ) .

(119)

Марковские случайные процессы часто используют для описания различных реальных физических случайных процессов и сигналов.

Примером марковского СП является винеровский случайный процесс, который описывает хаотическое движение частиц жидкости или газа при отсутствии внешних

воздействий: X (t) N (t1 )dt1 , где N (t) – это СП с

N (t)

и BN

(t1

, t2 )

(t2 t1 ) .

Для винеровского СП

0 и B

(t , t

)

min(t , t

) .

X (t)

1 2

ЛЕКЦИЯ 14

Спектральная плотность мощности случайного процесса. Теорема Хинчина–Винера. Эффективная ширина спектра случайного процесса и её связь с интервалом корреляции. Спектр и корреляционная функция белого шума.

При изучении детерминированных процессов часто применяют гармонический анализ

– это ряды Фурье для периодических сигналов и преобразования Фурье для непериодических сигналов. Аналогично, преобразования Фурье можно применять и для анализа случайных процессов.

Спектральная плотность мощности случайного процесса

Определим спектральную плотность любой реализации случайного процесса X (t) на временном интервале длительностью T выражением

SX ,T ( f )	T / 2
SX ,T ( f )	X (t) e j 2 f t dt , [В/Гц].
	T / 2

Тогда спектральная плотность мощности (СПМ) случайного процесса X (t) равна

		1			2
		1			2
GX	( f ) lim		SX ,T	( f )		, [Вт/Гц].	(120)
	T T

Следует отметить, что СПМ не содержит информации о фазо-частотном спектре СП.

Теорема Хинчина–Винера

Если случайный процесс не содержит регулярной составляющей, X (t) X (t) , то усреднённая по времени корреляционная функция и спектральная плотность мощности такого случайного процесса связаны друг с другом парой преобразований Фурье

GX ( f )

BX ( ) e j 2 f

[Вт/Гц],

(121)

BX ( ) GX ( f ) e j 2 f df

[Вт],

(122)

где

T / 2

BX () BX (t, t ) lim

BX (t, t )dt .

(123)

T T

Доказательство:

T / 2

2 lim

e j 2 f (t1 t2 ) dt dt

( f ) lim

X ,T

( f )

X ,T

( f ) S X ,T ( f ) lim

X (t ) X (t

)

T T

T / 2

lim

(t, t )dt e j 2 f d

BX () e j 2 f d .

Свойства:

T T

T / 2

1) площадь фигуры, ограниченной GX ( f ) , есть средняя мощность СП:

PX BX (0) GX ( f )df ;

(124)

2) из свойства чётности корреляционной функции BX ( ) следует, что

GX ( f ) Re BX () e j 2 f

d BX ( ) cos(2f )d 2 BX () cos(2f )d

(125)

–действительная и чётная функция частоты;

3)из свойства чётности СПМ GX ( ) следует, что

<<< < Предыдущая 1 2 3 45 / 155 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.201810.04 Mб48Книга ЭВМ.docx
#
10.06.2015222.21 Кб22ком. мен. лекции.doc
#
25.09.2019279.55 Кб19Команды общего назначения.doc
#
17.04.2019147.46 Кб18Компенс ст рег.doc
#
29.03.20161.46 Mб65Конспект Введение в спец. .pdf
#
10.06.20151.85 Mб112Конспект лекции по ТЭС.pdf
#
21.12.20182.42 Mб61Конспект лекций И-М.doc
#
10.06.2015900.61 Кб179Конспект лекций по дисц.ОИК. Часть 4..doc
#
29.03.20163.66 Mб322Конспект лекций по КГ.doc
#
10.06.20151.09 Mб76Конспект лекций по рекламе в ком. процессе..doc
#
10.06.20151.65 Mб32Конспект лекций по УК.docx