
Конспект лекции по ТЭС
.pdf
Спектральное представление сигналов в системах связи Спектры периодических сигналов. Ряд Фурье
Периодическую функцию x(t) , с периодом T можно разложить в ряд Фурье по ортогональным функциям cos(2f1kt) и sin(2f1kt) (гармоники частоты kf1 ):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2f1kt bk sin 2f1kt , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x(t) a0 |
ak |
|
|
|
|
|
|
|
|
(20) |
||||||||||||||||||||||||||||||||||||||||||||
|
f1 1/ T |
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
– частота первой гармоники, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
1 |
T / 2 |
|
|
|
|
|
2 |
|
T / 2 |
x(t) cos 2f1kt dt , |
|
|
|
|
|
|
|
2 |
T / 2 |
x(t) sin 2f1kt dt . |
|
|||||||||||||||||||||||||||||||||||||
|
a0 |
x(t)dt , ak |
|
|
|
|
bk |
|
(21) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
T |
T |
T |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
T / 2 |
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
||||
|
Ортогональность функций выполняется на интервале времени T / 2;T / 2 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
T / 2 |
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
||||
|
cos(2f1kt) cos(2f1lt)dt |
|
|
sin(2f1kt) sin(2f1lt)dt |
k l , |
cos(2f1kt)sin(2f1lt)dt 0 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
T / 2 |
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Совокупность коэффициентов ряда Фурье {ak , bk } называют спектром |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
периодического сигнала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Свойства коэффициентов ряда Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1) a k |
ak (чётные); |
|
|
|
|
2) b k |
bk (нечётные). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Ряд Фурье (20) можно записать в другой форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2f1kt k , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x(t) Ak |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(22) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
arctg bk |
/ ak . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
где A0 | a0 | , |
Ak |
ak2 bk2 |
, |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Согласно (22) сигнал x(t) |
можно представить в виде суммы гармонических колебаний |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
с частотами кратными основной частоте |
|
f1 , с амплитудами Ak |
и начальными фазами k . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Совокупность |
|
амплитуд |
Ak |
|
( k 0,1, 2,...) |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
образуют амплитудный спектр сигнала, а |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
совокупность |
фаз |
|
k |
– |
|
фазовый |
|
|
спектр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 f1 f2 |
f3 f4 f5 |
f |
|
||||||||||||||||||||||||||||||||||||||||||
сигнала. |
Спектр |
|
периодического |
|
|
|
|
|
сигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Рис. 5. Амплитудный |
спектр |
периодического |
|||||||||||||||||||||||||||||||||||||||||||||||||||
дискретный |
или |
|
линейчатый. |
|
|
|
|
Ak |
|
|
и |
|
|
k |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
сигнала |
для ряда Фурье с действительными |
|||||||||||||||||||||||||||||||||||||||||||||||||
определены только на положительных частотах. |
|
|
|
|
|
коэффициентами. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Комплексный ряд Фурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Ряд Фурье (22) можно представить и в комплексной форме, если воспользоваться |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
представлением cos(x) (e jx e jx ) / 2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
j 2 f1kt |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(23) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ck – комплексная амплитуда, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 T / 2 |
|
|
|
|
j 2 f1kt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ck |
|
|
|
|
|
|
|
|
|
|
|
x(t) e |
|
|
|
|
|
|
|
|
|
dt . |
|
|
|
|
|
|
|
|
|
|
|
|
(24) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Совокупность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ck |
образует амплитудный спектр, а k arg(Ck ) – фазовый спектр. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f5 f4 f3 f2 f1 0 f |
1 |
|
f2 f3 f4 f5 |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Рис. 6. Амплитудный спектр периодического сигнала для ряда Фурье с комплексными коэффициентами.
10

Свойства комплексной амплитуды:
1 1 *
1)C k 2 (a k jb k ) 2 (ak jbk ) Ck ;
2)связь с действительными коэффициентами ряда Фурье:
|
|
|
|
ak jbk |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
C0 |
a0 , |
Ck |
|
|
, при k 0 ; |
| C0 |
| A0 , |
Ck |
|
|
Ak |
; |
(25) |
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) амплитудный и фазовый спектры являются двусторонними по частоте. |
|
|
|||||||||||
Спектр непериодических сигналов. Преобразования Фурье
Разложение в ряд Фурье непериодической функции можно получить, если в ряде (23)
T или |
f1 0 . Тогда вместо ряда Фурье |
получим |
интеграл Фурье, |
а вместо |
коэффициентов ряда – функцию от частоты Sx ( f ) . |
Формулы, |
связывающие x(t) |
и Sx ( f ) |
|
друг с другом, называют преобразованиями Фурье:
|
|
|
x(t) |
Sx ( f ) e j 2 f t df (обратное преобразование Фурье), |
(26) |
|
|
|
|
|
|
Sx ( f ) x(t) e j 2 f t dt (прямое преобразование Фурье). |
(27) |
|
Функцию Sx ( f ) называют спектральной плотностью сигнала. Если сигнал имеет размерность напряжения вольт (В), то размерность спектральной плотности будет (В/Гц).
Модуль |
|
Sx ( f ) |
|
– амплитудный спектр, а arg Sx ( f ) x ( f ) – фазовый спектр сигнала. |
|
|
Свойства преобразования Фурье:
1)если сигнал x(t) – вещественный (не комплексный), то амплитудный спектр Sx ( f )
–чётная функция частоты, а фазовый спектр ( f ) – нечётная функция частоты;
2)если сигнал x(t) – вещественная и чётная функция, то Sx ( f ) – вещественная;
3)a x1 (t) b x2 (t) a Sx1 ( f ) b Sx2 ( f ) (преобразование Фурье – линейное преобразование);
4)x(t t0 ) Sx ( f ) e j 2 f t0 (спектр сигнала, задержанного на величину t0 );
|
|
|
|
|
1 |
|
|
|
|
f |
|
|
5) |
x(a t) |
|
|
Sx |
|
|
(масштабирование сигнала во времени – сжатие или растяжение); |
|||||
| a | |
|
|||||||||||
|
|
|
|
|
|
|
|
a |
|
|||
|
|
|
1 |
|
k |
|
|
|
|
|||
6) |
Ck |
|
|
Sx |
|
|
|
(связь со спектром периодического сигнала (преобразование 1 периода)); |
||||
T |
|
|
||||||||||
|
|
|
|
T |
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||
7) |
u(t) x(t) cos(2f0t) , |
Su |
( f ) |
|
Sx ( f f |
0 ) |
|
|
Sx ( f f0 ) ; |
|||||
2 |
2 |
|||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
8) |
u(t) x(t) sin(2f0t) , |
Su |
( f ) |
|
Sx ( f |
f0 ) |
|
|
|
Sx |
( f |
f0 ) ; |
||
2 j |
|
2 j |
||||||||||||
9) u(t) x(t) e j 2 f0t , |
Su ( f ) Sx ( f f0 ) ; |
|
|
|
|
|
|
|
||||||
10) свёртка двух сигналов:
|
|
|
Su ( f ) Sx ( f )Sg ( f ) . |
u(t) x(t) g(t) |
g( )x(t )d |
x( )g(t )d , |
|
|
|
|
|
11

Дельта-функция Дирака
Часто, при описании различных сигналов и их математических преобразований,
используется дельта-функция Дирака |
|
|
|
|
(t) |
|||
|
|
(t) ,t 0, |
|
|
|
1 |
||
0, |
t 0. |
|
|
– 0 |
t |
|||
Свойства дельта-функции: |
|
|
|
|
||||
|
|
|
|
|
|
Рис. 7. |
||
|
|
|
|
|
|
|
||
1) площадь дельта-функции равна единице: (t)dt 1; |
|
|
||||||
|
|
|
|
|
|
|
|
|
2) отсчётное свойство: x(t)(t t0 ) x(t0 )(t t0 ) ; |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
3) фильтрующее свойство: x(t)(t t0 )dt |
x(t0 )(t t0 )dt x(t0 ) ; |
|||||||
|
1 |
|
|
|
|
|
|
|
4) (at) |
(t) ; 5) S ( f ) 1 , откуда |
|
|
|
|
|
||
(t) e j 2 ft df |
|
cos(2 ft)df . |
||||||
|
||||||||
|
| a | |
|
|
|
|
|
||
|
|
|
|
|
|
|||
Спектральная плотность периодических сигналов
Спектральную плотность периодических сигналов невозможно непосредственно найти по формуле прямого преобразования Фурье, т.к. периодические сигналы имеют бесконечную длительность. Но её можно получить, если использовать дельта-функцию Дирака. Для этого разложим периодический сигнал в комплексный ряд Фурье
|
|
|
|
|
|
|
|
|
j 2 f1kt |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x(t) Ck e |
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 2 f t |
|
|
|
|
j 2 (kf1 |
f )t |
|
|||||
( f ) |
x(t) e |
dt |
|
|
e |
dt |
|||||||||
Sx |
|
|
Ck |
|
|
|
|||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||
или |
|
|
( f ) |
|
( f kf1 ) . |
|
|
|
(28) |
||||||
|
|
|
|
|
|
||||||||||
|
Sx |
Ck |
|
|
|
||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
Спектральная плотность периодического сигнала |
состоит из последовательности |
||||||||||||||
дельта-импульсов с комплексной амплитудой
равным частоте первой гармоники. Также можно показать, что
|
|
|
|
|
|
|
|
|
|
( f ) |
|
||||
|
Sx |
Ck |
|||||
|
|
|
|
|
k |
|
|
|
|
|
2 |
|
|
||
( f ) |
|
||||||
Sx |
|
Ck |
|||||
|
|
|
|
|
k |
|
|
Ck , следующих друг за другом с интервалом
|
( f kf1 ) . |
(29) |
|
|
2 ( f |
kf ) . |
(30) |
|
|||
|
|
1 |
|
Вывод: преобразования Фурье по сравнению с рядом Фурье являются более общими преобразованиями, поскольку их можно применять как для периодических, так и для непериодических сигналов.
12
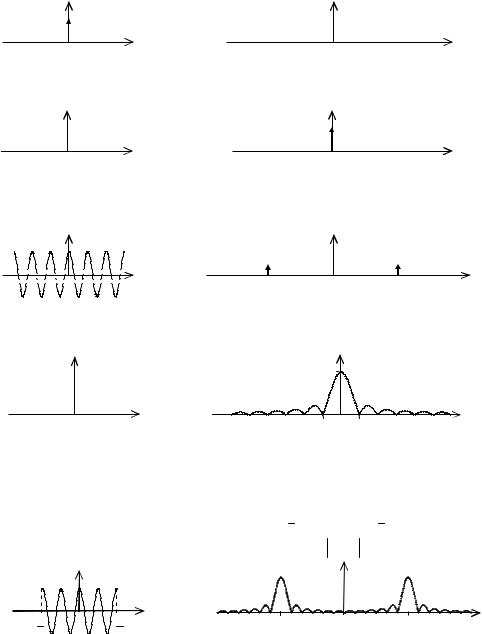
Примеры математических моделей сигналов и их спектров
1) |
|
|
|
|
|
|
|
|
x(t) A (t) , |
|
|
|
|
|
|
|
|
|
Sx ( f ) A ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
x(t) A , |
|
|
|
|
|
|
|
|
|
Sx ( f ) A ( f ) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3) x(t) Acos(2f0t) – гармоническое колебание, Sx ( f ) |
|
A |
|
|
( f |
f0 ) |
A |
( f |
f0 ) ; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
A/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A/2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
f0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f0 |
|
|
|
|
|
|
|
f |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin(f ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
4) x(t) – одиночный прямоугольный импульс, |
Sx ( f ) A |
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
Sx ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
1 |
|
0 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
f |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Вывод: чем шире во времени импульс, тем уже его спектр и наоборот.
5) u(t) – отрезок гармонического колебания, радиоимпульс:
u(t) x(t) cos(2f0t) , |
|
( f ) |
1 |
|
( f |
f0 ) |
1 |
|
( f f0 ) ; |
|
|||
Su |
2 |
Sx |
2 |
Sx |
|
||||||||
|
|
u(t) |
|
|
|
|
|
|
Su ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
t |
f0 |
|
|
|
0 |
|
|
f0 |
f |
2 |
2 |
|
|
|
|
|
|
||||||
Энергия и средняя мощность сигналов
К энергетическим характеристикам сигналов относят энергию и мощность сигнала. От них зависит качество и дальность связи, стоимость и сложность приёмных и передающих устройств, а также другие, не менее важные характеристики систем связи. Для удобства в ТЭС принято, что сопротивление нагрузки нормируется и равно 1 Ом.
Энергию и мощность сигнала, длительность которого равна T и действующего на интервале времени ( T / 2;T / 2) , находят по следующим формулам:
E |
T / 2 |
x2 (t)dt , |
P |
1 |
T / 2 |
x2 (t)dt . |
(31) |
|
|
T |
|
||||||
x |
|
x |
|
|
||||
T / 2 |
|
|
T / 2 |
|
|
|||
|
|
|
|
|
|
Энергия имеет размерность В2с/1 Ом = Вт с = Дж , а мощность – В2/1 Ом = Вт . Если длительность сигнала T , то
13
|
|
|
|
|
2 |
|
|
|
1 |
T / 2 |
|
2 |
|
|
E |
x |
|
|
x |
|
(t)dt , |
P lim |
|
|
x |
|
(t)dt . |
(32) |
|
|
|
|
||||||||||||
|
|
|
|
|
x |
T T |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
Физические сигналы, существующие в природе, теоретически ограничены и по времени, и по частоте, поэтому они имеют конечную энергию Ex и мощность Px 0 .
Рассмотрим некоторые математические модели сигналов. Первая модель – это одиночный прямоугольный импульс, который не является физическим сигналом, поскольку спектр его неограничен по частоте. Вторая модель – периодический сигнал. Он также не является физическим сигналом, т.к. он неограничен во времени.
Хотя рассмотренные модели сигналов в природе не существуют, но они являются удобной математической заменой реальных физических сигналов. Преимуществом их использования является то, что над ними легче производить математические преобразования.
Равенство Парсеваля
Равенство Парсеваля для сигналов с конечной энергией и периодических сигналов:
|
|
2 |
|
|
|
|
2 |
|
|
|
1 |
T / 2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ex |
x |
|
(t)dt |
|
Sx |
( f ) |
df , |
|
Px |
|
|
|
x |
|
(t)dt |
|
Ck |
|
. |
(33) |
|
|
|
T |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
T / 2 |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обобщённое равенство Парсеваля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) y* (t)dt |
|
|
|
|
|
|
|
|
|
|
(34) |
|||
|
|
|
|
|
|
Sx ( f ) S y ( f )df . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14
ЛЕКЦИЯ 4
Аналитический сигнал. Преобразования Гильберта. Квазигармоническое и комплексное представления узкополосных сигналов и его применения в технике связи. Огибающая, фаза,
мгновенная частота, квадратурные компоненты сигнала. Сопряженный сигнал. |
|
Обобщением действительных функций являются комплексные функции. |
|
Аналитический сигнал – это комплексный сигнал, который равен |
|
u(t) u(t) ju(t) , |
(35) |
где u(t) – исходный действительный сигнал, u(t) – преобразование Гильберта от u(t) . Преобразования Гильберта (ПГ) – это пара линейных обратимых преобразований
1 u( )
u(t) H u(t) t d (прямое),
1 1 u( )
u(t) H u(t) t d (обратное).
Преобразование Гильберта можно реализовать линейным фильтром с ИХ
g() 1 ( ),
которая соответствует передаточной функции
(36)
(37)
(38)
|
|
|
|
|
j 2 f |
|
|
|
|
|
|
|
|
d j sign( f ) , |
(39) |
||
|
K ( f ) g( ) e |
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
, при x 0, |
|
||||
где sign( f ) |
– знак f , т.е. sign(x) |
|
|
|
||||
|
|
|||||||
| x | |
|
|
|
|
|
|||
|
|
|
0, при x 0. |
|
||||
|
|
|
|
|||||
u(t) |
|
ПГ |
|
u(t) |
|
Su ( f ) |
|
|
Su ( f ) |
||
|
|
|
|||
g( ) 1/( ) |
|||||
|
|
||||
K ( f ) j sign( f )
Рис. 8. Преобразователь Гильберта.
Спектр сигнала на выходе ПГ равен
|
|
|
|
( f ) . |
(40) |
Su ( f ) K ( f )Su |
( f ) j sign( f )Su |
||||
При подаче на вход этого фильтра сигнала u(t) , на выходе получим сопряжённый по |
|||||
Гильберту сигнал u(t) . Т.к. |
ИХ |
ПГ |
g( ) существует |
при 0 |
и имеет бесконечную |
длительность, то такой фильтр физически нереализуемый. Для его реализации необходимо ограничить ИХ по времени, а интегрирование выполнять с задержкой входного сигнала.
Свойства аналитического сигнала:
1. Спектр аналитического сигнала содержит только положительные частоты:
2Su ( f ), |
f |
0; |
|
|
0, |
|
f |
0; |
|
|
|
|
f |
0; |
S |
|
|
(0), |
f |
0; |
(41) |
Su ( f ) Su ( f ) jSu ( f ) Su (0), |
( f ) Su |
|||||||||
|
0, |
f 0; |
|
u |
|
|
|
|
|
|
|
|
|
2Su ( f ), f 0. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2. Сигналы u(t) и u(t) |
ортогональные: |
|
|
|
|
|
|
|
|
|
|
|
2 sign( f )df |
|
|
u(t)u(t)dt Su ( f ) S*u ( f )df |
|
j |
Su ( f ) |
0 , |
(42) |
||
|
|
|
|
|
|
|
|
где Su ( f ) 2 sign( f ) – нечётная функция, а интеграл по симметричным пределам от нечётной функции равен нулю.
15

3. Над аналитическими сигналами просто выполнить преобразование частоты и фазы: s(t) u(t) e j ( 0t 0 ) . (43)
Для получения действительного сигнала следует выполнить последовательность шагов:
|
|
|
|
|
|
|
|
|
|
j ( 0t 0 ) |
|
|
|
. |
|
(44) |
|||||||
u(t) u(t) s(t) u(t) e |
|
s(t) Re s(t) |
|
||||||||||||||||||||
В результате преобразований получим сигнал |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
s(t) u(t) cos(0t 0 ) u(t)sin(0t 0 ) . |
|
|
|
|
|
|
|
|
|
(45) |
|||||||||||||
0 |
|
Su ( f ) |
|
|
|
|
f |
|
|
|
0 |
|
Su ( f ) |
|
|
|
|
f |
|
||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Ss ( f ) |
|
|
|
|
|
|
|
|
|
Ss ( f ) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
f0 |
f |
|
f0 |
0 |
|
|
|
|
|
|
f0 |
f |
|
|||
Рис. 9. Амплитудный спектр аналитического и действительного сигналов, а также |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
сдвиг их спектров по частоте. |
|
|
|
|
|
|
|
|
|
|
|
||||
4. ПГ от косинуса и синуса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
H[cos(2 ft)] sin(2 ft) sign( f ) . |
|
|
|
|
|
|
|
|
|
|
(46) |
||||||||
|
|
|
H[sin(2 ft)] cos(2 ft) sign( f ) . |
|
|
|
|
|
|
|
|
|
|
(47) |
|||||||||
5. Скалярное произведение двух сигналов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(t)(t)dt |
u(t) (t)dt . |
|
|
|
|
|
|
|
|
|
|
(48) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
u(t)(t)dt u(t)(t)dt . |
|
|
|
|
|
|
|
|
|
|
(49) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ортогональность в усиленном смысле |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Сигналы u(t) и v(t) ортогональны в усиленном смысле, если |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(t)v(t)dt 0 и |
u(t)v(t)dt 0 . |
|
|
|
|
|
|
|
|
|
|
(50) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если сигналы ортогональны |
в усиленном смысле, |
то ортогональность |
сигналов |
||||||||||||||||||||
сохранится также при произвольном фазовом сдвиге одного из сигналов. Например, если u (t) u(t) cos( ) u(t) sin( ) ,
|
|
|
|
|
то |
u (t)(t)dt cos( ) u(t)v(t)dt sin( ) u(t)v(t)dt 0 . |
(51) |
||
|
|
|
|
|
|
Полосовой сигнал |
|
fmin до fmax , называют полосовым. |
|
|
Сигнал, занимающий некоторую полосу частот от |
|||
Узкополосный сигнал
Сигнал u(t) можно считать узкополосным, если ширина его спектра fс fmax fmin
во много раз меньше центральной частоты спектра сигнала f0 ( fmax fmin ) / 2 , т.е. f f0 или fс / f0 1 . Если это условие не выполняется, то сигнал является широкополосным.
|
|
Su ( f ) |
|
f |
|
|
fс |
fmax fmin |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
f0 ( fmax |
fmin ) / 2 |
|
f0 |
0 |
|
|
|
|
|
|
f |
|
|
fmin f0 fmax |
|
|
||||||
Рис. 10. Амплитудный спектр узкополосного сигнала. |
|
|
|
||||||
16

Квазигармоническое представление узкополосного сигнала
Узкополосный сигнал можно представить в виде квазигармонического сигнала:
u(t) A(t) cos(0t (t)) , |
(52) |
где A(t) – мгновенная амплитуда сигнала или огибающая сигнала, |
(t) – мгновенная |
фаза сигнала, f0 – центральная частота спектра сигнала. A(t) и (t) медленно меняющиеся во времени сигналы по сравнению с изменением функции cos(0t) .
Представление узкополосного сигнала через квадратурные компоненты: |
|
||||||||||
|
u(t) x(t) cos(0t) y(t) sin(0t) , |
(53) |
|||||||||
где x(t) A(t) cos( (t)) и y(t) A(t) sin( (t)) |
– квадратурные компоненты. |
|
|||||||||
Связь квадратурных компонент с огибающей и фазой: |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
A(t) |
|
x2 (t) y2 (t) 0 , |
(t) arctg( y(t) / x(t)) . |
(54) |
|||||||
Полная фаза и мгновенная частота: |
|
|
|
||||||||
(t) 0t (t) 0t arctg( y(t) / x(t)) , |
(55) |
||||||||||
(t) |
d (t) |
|
|
|
y (t)x(t) x (t) y(t) |
. |
(56) |
||||
|
0 |
|
|||||||||
|
|
|
dt |
|
|
x2 (t) y2 (t) |
|
||||
Представление узкополосного сигнала в комплексной форме
Преобразование Гильберта узкополосного сигнала выполняется достаточно просто:
H u(t) H A(t) cos(0t (t)) A(t) sin(0t (t)) . |
(57) |
||
H u(t) H A(t) sin(0t (t)) A(t) cos(0t (t)) . |
(58) |
||
Это эквивалентно |
задержке сигнала |
u(t) на время t0 1/(4 f0 ) : |
u(t) u(t t0 ) , что |
соответствует фазовому |
сдвигу на / 2 . |
Устройство, которое на своём выходе выдаёт |
|
сопряжённые по Гильберту сигналы, называется квадратурным расчепителем.
u(t)
u(t)
ПГ |
u(t) |
|
|
Рис. 11. Квадратурный расчепитель узкополосного сигнала (фазорасчепитель).
С учётом сказанного, узкополосный сигнал можно представить в комплексной форме:
u(t) u(t) ju(t) A(t) e |
j ( 0t (t )) |
|
j 0t |
, |
(59) |
||
|
A(t) e |
|
|||||
где |
|
|
|
|
|
|
|
|
j (t ) |
x(t) jy(t) |
|
|
(60) |
||
A(t) A(t) e |
|
|
|
||||
– комплексная амплитуда или низкочастотный эквивалент узкополосного сигнала.
Узкополосный сигнал полностью определяется его квадратурными компонентами x(t) и y(t) , поскольку
u(t) Re u(t) x(t) cos(0t) y(t) sin(0t) . |
(61) |
Поэтому, чтобы выполнить фильтрацию или другое преобразование над узкополосным сигналом, достаточно это преобразование применить к его квадратурным компонентам. Обработку квадратурных компонент выполнить гораздо проще, чем узкополосного сигнала.
17
ЛЕКЦИЯ 5
Дискретное представление сигналов. Дискретизация функций непрерывного аргумента и ее применения в технике связи. Теорема Котельникова для сигналов с финитным спектром. Восстановление непрерывного сигнала по его отсчетам. Погрешности при восстановлении реальных сигналов и их причины. Квантование отсчётов по уровню и кодирование. Структурные схемы АЦП и ЦАП.
Для цифровой обработки аналоговых сигналов современные системы цифровой связи содержат в своём составе аналогово-цифровые и цифро-аналоговые преобразователи (АЦП и ЦАП). Цифровые сигналы имеют ряд преимуществ перед аналоговыми сигналами, а именно, их удобно хранить (современные микросхемы памяти имеют малые размеры, а их ёмкость существенно превосходит магнитные носители информации), над ними легко производить различные преобразования или цифровую обработку (цифровая фильтрация, сжатие их до меньшего размера без потери и с потерей информации и др.), они более устойчивы к воздействию помех (для защиты от ошибок можно использовать помехоустойчивое кодирование).
Основной операцией аналогово-цифрового преобразования является дискретизация по времени – это представление непрерывной функции последовательностью её мгновенных значений или отсчётов. Устройство, выполняющее дискретизацию, называют
дискретизатором.
Для точного представления непрерывного сигнала x(t) на некотором интервале времени необходимо знать отсчёты этого сигнала во всех точках внутри интервала. Теоретически число таких отсчётов равно бесконечности. Но для функций, имеющих финитный (конечный) спектр, число необходимых отсчётов можно существенно сократить.
Теорема Котельникова. Любой сигнал, спектр которого сосредоточен в полосе частот
f (Fс ; Fс ) , а за пределами этой полосы спектр его равен |
нулю, можно |
полностью |
||
восстановить по его отсчётам, взятым через интервал времени t 1/(2Fс ) . |
|
|
||
Интервал времени t называют интервалом дискретизации, а величину, |
fд 1/ t |
– |
||
частотой дискретизации. |
|
|
|
|
Идеальная дискретизация |
|
|
|
|
При идеальной |
дискретизации некоторого сигнала x(t) |
дискретизированный |
по |
|
времени сигнал xд (t) |
получается в результате перемножения исходного сигнала x(t) |
на |
||
решётчатую функцию xр (t) , состоящую |
из последовательности дельта-импульсов, |
|
следующих друг за другом с постоянным интервалом времени t : |
|
|
|
|
|
xд (t) x(t)xр (t) x(t) (t |
k t) xk (t k t) . |
(62) |
k |
k |
|
где xk x(k t) – отсчёт сигнала x(t) в момент времени t k t .
Найдём спектральную плотность дискретизированного сигнала. Произведение двух функций во временной области соответствует свёртке их спектральных плотностей в частотной области. Поэтому
|
|
|
|
|
|
|
Sxд ( f ) Sx ( )Sxр ( f )d . |
(63) |
|||
|
|
|
|
|
|
Поскольку xр (t) – периодическая функция с периодом равным t , то |
|
||||
|
|
|
|
|
|
|
( f |
k fд ) fд ( f k fд ) |
(64) |
||
Sxр |
( f ) Ck |
||||
|
k |
|
|
k |
|
|
|
|
|
|
|
и |
Sxд ( f ) fд Sx ( f k fд ) . |
(65) |
|||
k
18
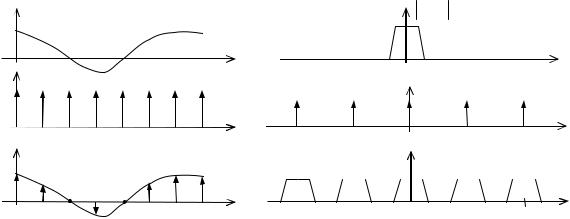
Следовательно, спектр дискретизированного сдвинутых относительно друг друга на величину fд
x(t)
t
xр (t)
0 t |
t |
2 fд |
xд (t)
0 t |
t |
2 |
|
fд |
|
Рис. 12.
сигнала – периодический и состоит из спектров исходного сигнала.
Sx ( f )
|
|
|
Fс |
0 Fс |
|
|
|
|
|
f |
|||||
fд |
fд |
0 |
|
|
Sxр ( f ) |
|
fд |
|
2 fд |
f |
|||||
|
|
|
|
||||||||||||
|
Sxд ( f ) |
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
Fс |
|
|
|
|
|
|
|
|
|
|
2 fд |
f |
|
|
|
|
|
|
|
|
|
||||||||
д |
0 Fс |
|
fд |
|
|||||||||||
Из сказанного следует, что для восстановления непрерывного сигнала x(t) достаточно
сигнал |
xд (t) |
пропустить через ФНЧ (аналоговый) с коэффициентом передачи |
K0 t в |
||||
полосе |
f [Fс ; Fс ] и частотой среза |
fср [Fс ; fд Fс ]. На выходе фильтра |
получим |
||||
полностью |
восстановленный |
сигнал |
x(t) . |
Этот фильтр называют |
фильтром- |
||
восстановителем (ФВ). |
x(t) на выходе фильтра-восстановителя можно найти как |
||||||
Восстановленный сигнал |
|||||||
результат свёртки импульсной |
характеристики |
фильтра-восстановителя g( ) |
и |
входного |
|||
сигнала xд (t) :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x(t) g( )xд (t )d xk |
g( )(t k t)d xk g(t k t) . |
|
|||||||||||||||||
|
|
k |
|
|
|
|
|
k |
|
|
|
|
|
|||||||
Если в качестве фильтра-восстановителя |
|
используется |
идеальный |
ФНЧ с ИХ |
||||||||||||||||
g( ) t |
sin(2f |
ср ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
, то восстановленный сигнал на его выходе будет равен |
|
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
sin(2fср (t k t)) |
|
|
|
|||||||
|
|
|
x(t) xд (t) g(t) (2 fср t) xk |
|
|
|
|
|
|
|
, |
|
(66) |
|||||||
|
|
|
2 fср (t k t) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||||
В случае, |
если fср fд / 2 |
( fд 2Fс ), |
то получим разложение |
сигнала |
x(t) в ряд по |
|||||||||||||||
ортогональным базисным функциям k (t) g(t k t) |
sin(fд (t k t)) |
, который называют |
||||||||||||||||||
fд (t k t) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
рядом Котельникова: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
sin(fд (t k t)) |
|
|
|
|
|
|
|||||
|
|
|
|
|
x(t) xk k (t) xk |
|
|
|
|
|
. |
|
|
|
|
(67) |
||||
|
|
|
|
|
fд (t k t) |
|
|
|
|
|||||||||||
|
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|||||||
19
