Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект лекции по ТЭС

.pdf

Скачиваний:

112

Добавлен:

10.06.2015

Размер:

1.85 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>


	BX () GX ( f ) cos(2f )df				2 GX ( f ) cos(2f )df	GX ,0 ( f ) cos(2f )df ,	(126)
					0	0
где	GX ,0	2GX ( f ),		f 0,
где	GX ,0	( f )	0,	– односторонняя СПМ (спектральная плотность мощности,
			0,	f 0

определённая на положительных частотах).

Эффективная ширина спектра СП Fэ определяется как ширина полосы частот GX ,0 ( f ) , в которой сосредоточенна основная часть мощности СП, например, 90…99%. Её можно найти из уравнения

Fэ
GX ,0 ( f )df	GX ,0 ( f )df BX (0) , где 0,9...0,99 .	(127)
0	0

Связь между кор и Fэ определяется соотношением

кор Fэ K , где K – константа порядка единицы для простых сигналов. Из этого соотношения следует, что Fэ K / кор , т.е. чем уже корреляционная функция, тем шире энергетический спектр СП и наоборот.

GX ,0 ( f )

90% PX

0 Fэ

Рис. 33. Определение эффективной ширины спектра СП.

Белый шум

Белый шум является распространённой и важной для теории связи моделью случайного процесса. Он широко используется при описании различных моделей каналов связи с шумом. Его можно использовать для формирования случайных процессов с заданной корреляционной функцией или спектральной плотностью мощностью.

Белый шум – это случайный процесс с постоянной спектральной плотностью мощности на всех частотах. Шум назван белым, потому что такой же спектр имеет белый

свет. Если N (t) – белый шум, то N (t) 0 и GN ( f ) N0 / 2 . Константа N0 – это односторонняя (заданная на положительных частотах) спектральная плотность мощности белого шума.

Корреляционная функция белого шума равна

BN ( ) GN

( f ) e j 2 f df

e j 2 f df

( )

или BN (t1, t2 )

(t2 t1 ) .

(128)

Из выражения для корреляционной функции белого шума следует, что его различные

сечения некоррелированные, а интервал корреляции равен нулю.

GN ( f )

BN ( )

N0 / 2

Рис. 34. Энергетический спектр и корреляционная функция белого шума.

В природе белого шума в чистом виде не существует, т.к. его средняя мощность равна

PX BN (0) .

Он является

математической

идеализацией некоторого

реального

физического процесса. Многие физические процессы можно приближённо считать белым шумом. Например, тепловой шум резисторов (дробовый шум), который имеет равномерный

спектр до частот порядка 1012 Гц, математически можно описывать в виде белого шума. Отметим, что кроме белого существуют также розовый и коричневый шум. Для

розового шума СПМ в заданной полосе частот убывает с ростом частоты по закону G( f ) 1/ f . Розовый шум называют также фликкер-шумом от англ. flicker – мерцание. Он описывает медленные флуктуации электрических токов и напряжений. Для коричневого шума СПМ убывает по закону G( f ) 1/ f 2 .

ЛЕКЦИЯ 15

Полосовой и узкополосный случайные процессы. Гауссовский узкополосный случайный процесс: распределение огибающей и фазы при отсутствии и наличии регулярной составляющей (релеевское и райсовское распределения). Корреляционные функции и спектральные плотности мощности квазибелого и узкополосного квазибелого шума. Представление случайных процессов с помощью рядов. Разложение в ряд Карунена–Лоэва.

Полосовой случайный процесс

Случайный процесс, занимающий некоторую полосу частот от fmin до fmax , называют

полосовым.

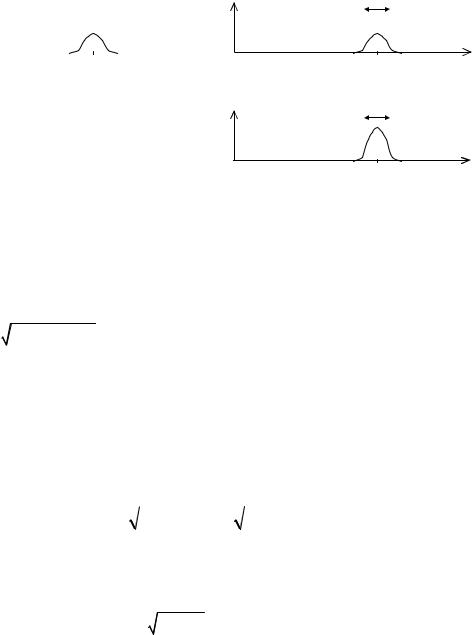
Узкополосный случайный процесс

Случайный процесс называется узкополосным, если его энергетический спектр

сосредоточен в относительно узкой полосе частот					около некоторой			частоты	f0 . Если
указанное условие не выполняется, то СП называют широкополосным.
				GU ( f )		f


		f0	0		fmin f0		fmax	f
	f	fmax fmin		GU ,0 ( f )		f
	f	fmax fmin
	f0 ( fmax fmin ) / 2

			0		fmin f0 fmax			f
		Рис. 35. Энергетический спектр узкополосного СП.
Если f –		ширина полосы	частот СПМ		случайного		процесса, то		условие

узкополосности можно определить неравенством f f0 или f / f0 1.
Узкополосный СП можно представить в виде квазигармонического СП
где	U (t) A(t) cos(0t (t)) X (t) cos(0t) Y (t) sin(0t) ,	(129)
где

A(t)	X 2 (t) Y 2 (t) – огибающая узкополосного СП, A(t) 0 ,

(t) arctg(Y (t) / X (t)) – случайная фаза узкополосного СП,

X (t) A(t) cos( (t)) и Y (t) A(t) sin( (t)) – квадратурные компоненты СП.

Гауссовский узкополосный СП

Если квадратурные компоненты узкополосного СП X (t) и Y (t) – независимые гауссовские СП с равными дисперсиями 2 2X Y2 , то совместная плотность вероятности любых его сечений равна

wX ,Y (x, y) wX (x)wY ( y)	1	e

	2 2
	2 2

где X и Y – сечения СП X (t) и Y (t) .

( x mX )2	1			( y mY )2	1		( x mX )2 ( y mY )2
2 2	1			2 2	1		2 2	,	(130)
			e			e
					22
		22			22

Мгновенные значения огибающей и фазы СП связаны со значениями квадратурных компонент функциональными зависимостями (переход от декартовых координат к полярным):

a	x2 y2 , arctg( y / x) .	(131)
x a cos( ) , y a sin( ) .		(132)

Известно, что при переходе к полярным координатам dxdy adad .

Тогда

(x, y)

(133)

(a, ) w

(a cos , a sin )

a w

X ,Y

(a cos , a sin )

X ,Y

(a, )

(a cos mX )2 (asin mY )2

или

wA, (a, )

2 2

a 0 ,

(134)

Одномерная плотность вероятности огибающей и фазы гауссовского СП равны

wA (a) wA, (a, )d ,

w () wA, (a, )da .

(135)

Некоторые частные законы распределения огибающей узкополосного гауссовского СП:

1. При mX

mY 0 закон распределения огибающей называется релеевским:

(a)

2 2

, a 0 .

(136)

При этом фаза имеет равномерное распределение:

, при ,

(137)

w ( ) 2

иначе.

2. Если mX

и mY одновременно не равны нулю,

то закон распределения огибающей

называется райсовским или обобщённым релеевским:

a2 mX2 mY2

2 2

wA (a)

(138)

где

I0 (x)

e x cos( ) d

– модифицированная функция Бесселя нулевого порядка.

В этом случае узкополосный СП можно представить в виде суммы

U (t) U (t) uр (t) X (t) cos(0t) Y (t) sin(0t) uр (t) ,

(139)

где

uр (t) mX cos(0t) mY sin(0t) aр cos(0t р ) – неслучайная

или

регулярная

составляющая СП с амплитудой a

и начальной фазой

arctg(m / m

) .

Квазибелый шум

Случайный процесс с равномерной СПМ в полосе частот ( F; F ) называется

квазибелым шумом.

Квазибелый шум можно получить из белого шума, если последний пропустить через

идеальный ФНЧ с частотой среза

fср

коэффициентом передачи

1. СПМ

случайного процесса X (t) на выходе такого фильтра равна

, при | f | F,

GX ( f )

K ( f )

GN ( f )

K ( f )

(140)

0, иначе,

а корреляционная функция

sin(2F)

BX ( )

e j 2 f df

N0 F

(141)

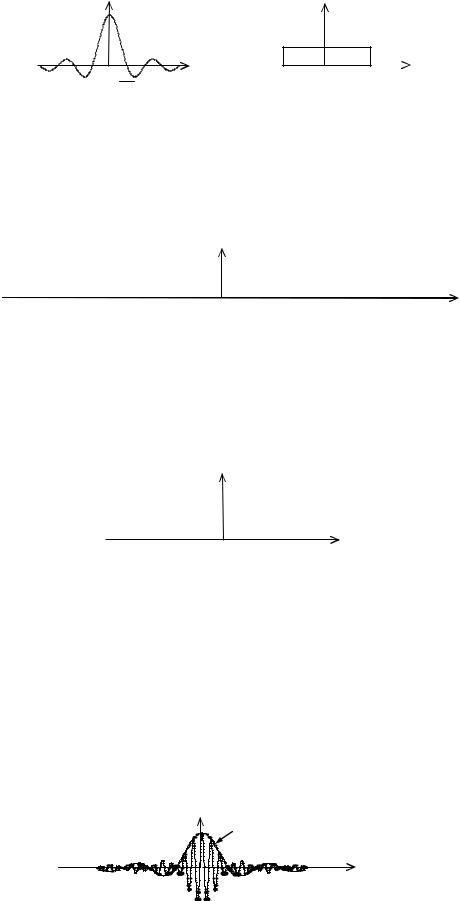
Случайный процесс X (t) является квазибелым шумом.

	BX ( f )				GX ( f )
	N0 F
					N0 / 2
	0 1		F	0	F	f
	2F
	Рис. 36. Корреляционная функция и СПМ квазибелого шума.
Особенностью	квазибелого	шума	является	то,	что его	средняя мощность
PX BX (0) N0 F не равна бесконечности как у белого шума, а сечения, отстоящие друг от
друга на интервал k	k /(2F ) , где k 1, 2,... , некоррелированные, т.к. BX (k / 2F ) 0 .

Узкополосный квазибелый шум

Энергетический спектр узкополосного квазибелого шума представлен на следующем рисунке.

GU ( f )

N0 / 2

f0 f0 F

Рис. 37. Энергетический спектр узкополосного квазибелого шума.

Узкополосный квазибелый шум U (t)

со спектральной плотностью мощности N0 / 2

можно выразить через квадратурные компоненты X (t) и Y (t) :

U (t) X (t) cos(0t) Y (t) sin(0t) ,

(142)

где X (t) и Y (t) – независимые стационарные СП с

0 ,

BX ( ) BY ( )

X (t)

Y (t)

X (t)Y (t)

и GX ( f ) GY ( f ) N0 в полосе частот [ F; F ] .

GX ( f ),GY ( f )

Рис. 38. Энергетический спектр квадратурных компонент узкополосного квазибелого шума.

Корреляционная функция случайного процесса U (t) равна

~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~

BU () BU (t, t ) BX (t, t ) cos(0) BX ( ) cos(0) .

(143)

Поскольку BU (t, t ) BU ( ) , то квазибелый шум – стационарный СП.

Спектральную плотность мощности узкополосного квазибелого шума можно выразить через спектральную плотность мощности одной из его квадратурных компонент по формуле

GU ( f )	1	GX ( f f0 ) GX ( f f0 ) .	(144)
	2

Корреляционная функция	BX ( ) является огибающей		корреляционной функции

узкополосного квазибелого шума BU ( ) .

2N0 F	BU ( f )
2N0 F	BX ( f )
0

Рис. 39. Корреляционная функция узкополосного квазибелого шума.

Представление СП с помощью рядов

Любой СП процесс на интервале t ( T / 2;T / 2) можно разложить в обобщённый ряд Фурье со случайными коэффициентами:

		T / 2
X (t) k k (t) ,	vk		X (t) k (t)dt ,	(145)
k 0		T / 2
где k (t) – ортонормированные	детерминированные функции, vk			– случайные
коэффициенты ряда.

Следовательно, для полного описания случайного процесса достаточно задать закон распределения всех случайных коэффициентов, полученных при его разложении в обобщённый ряд Фурье.

Для большинства случайных процессов, описывающих реальные физические процессы, с ростом номера k дисперсия коэффициентов ряда стремится к нулю. Поэтому такие случайные процессы описываются конечным числом случайных коэффициентов ряда.

Разложение в ряд Карунена–Лоэва

Представление СП в виде обобщённого ряда Фурье с некоррелированными коэффициентами называется каноническим разложением Карунена–Лоэва.

Для некоррелированности коэффициентов ряда vk должно выполняться равенство

	2	, k i,
vk vi k2	k i k	k i,
	0,	k i,

где 2k D vk – дисперсия vk . Тогда

	T / 2 T / 2				T / 2 T / 2
vk vi		X (t1 ) X (t2 ) k (t1 ) i (t2 )dt1dt2				BX (t1, t2 ) k (t1 ) i (t2 )dt1dt2 .	(146)
	T / 2 T / 2				T / 2 T / 2
Следовательно, функции k (t) должны удовлетворять интегральному уравнению
			T / 2
			BX (t1, t2 ) k (t1 )dt1		k2 k (t2 ) .		(147)
			T / 2
Используя разложение Карунена–Лоэва, легко выразить математическое ожидание и
корреляционную функцию через ортонормированные функции ряда:

				mX (t) mX ,k k (t) ,			(148)
				k 0

			BX (t1,t2 ) k2 k (t1 ) k (t2 ) ,				(149)

k 0

где mX ,k M vk .

Условие некоррелированности коэффициентов значительно упрощает анализ случайных процессов. Так, например, для гауссовского СП коэффициенты ряда будут не только некоррелированными и гауссовскими, но и независимыми.

Если случайным процессом является белый шум, то для разложения его в ряд Карунена–Лоэва на интервале (0;T ) подойдут любые ортонормированные функций, например, гармонические функции ряда Фурье. Для разложения в ряд Карунена–Лоэва квазибелого шума подойдут базисные функции ряда Котельникова.

ЧАСТЬ 2 ЛЕКЦИЯ 1

Каналы электросвязи. Их основные виды и классификация по различным признакам. Преобразования сигналов в непрерывных каналах. Основные характеристики непрерывных каналов во временной и частотной областях импульсные характеристики, передаточные функции, АЧХ и ФЧХ. Основные модели каналов.

Канал ! "# "$%!&'$&% ($) " & *&+&'$,-($), " (.$& /#+ 0"- )/- $($),'& &1!,/ 2$3) ) 2-" ' ,2& & "$2.-+& ,!,/. /, &*&4&( 0"- (,+/&'!.2 (&+!, ,2

Классификация каналов по назначению систем связи

+, & &2 "& " !,+!,'$!&- & "$2 -+& ,!,/. )$/-"- !, "$/$* !!.$ "$/$1(,*!.$+ 1$5,!&-"$/$&+& !!.$ $($),'& ),!!.% "$/$2$"(&'$&$& )(

Классификация каналов по среде распространения сигналов

+, & &2 "& " (, ( "(,!$!&-&1!,/ 6 )! 2 ( "(,! "$&/& /&!&-2-+& ,!,/. )$/-"- !, ,!,/. (,)&-+& 7 "!& .$ & )( 8 & ( )! 9 -+& 7 ,6$/#!.$/ !! : "&'$&$/&!&&-+& /! )!.$; "(, ". & )( 8

Классификация каналов по диапазону длин волн и частот

$# )&, ,+ ! & /#+$2.% ', " " / ! )$/-" !, / . 1(,!&'!.$ ', " ". " (.% "/&',0"- )( 1 " )( 1, <= (,+ > /# ', " " 9 f 1,(2 !&'$1

/$6,!&- -+,!, )/&!, /!. c ? f 1)$ c A <=@ 2? ( "# $", 6 )! 2 ( "(,! "$ " (,+)$/$!&$ ( &+ )-" & )&, ,+ ! )/&! /! 7",6/&4, Ошибка!

Источник ссылки не найден.8

,6/&4, < /, &*& ,4&-,!,/ )&, ,+ !,2 )/&! /! & ', " "

Наименование волн	Диапазон волн	Наименование частот	Диапазон частот
$, &/ 2$"( .$	<== <= 2	; 7 '$!# !&+ &$8	A A= B4
&/ 2$"( .$ 7 8	<= < 2	; 7!&+ &$8	A= A== B4
B$" 2$"( .$ 7 8	<=== <== 2	; 7 ($)!&$8	A== A=== B4
$,2$"( .$ 7 8	<== <= 2	; 7 . &$8	A A= B4
$"( .$ 7C 8	<= < 2	; 7 '$!# . &$8	A= A== B4
$4&2$"( .$ 7C 8	<== <= 2	C ; 7 /#"(, . &$8	A== A=== B4
,!"&2$"( .$ 7C 8	<= < 2	; 7$(% . &$8	A A= BB4
&//&2$"( .$ 7C 8	<= < 22	; 7 (,9!$. &$8	A= A== BB4
$4&2&//&2$"( .$	< = < 22	B>; 71& $( . &$8	A== A=== BB4

,)&-+# 5$" /-$"- 2 5#0 D/$"( 2,1!&"!.% /! )&, ,+ !$ ', " " " <== B4 ) A= BB4 ( )!.% "$/$* !!.% /&!&-% -+& & /#+ 0"- D/$"(&'$&$ /$6,!&- ', " ",2& ) < B4 " 2 '" !, 6 /$$ . &% ', " ",% ($+ +(, ",$" +," %,!&$ & E 2 /&!&& 7 ",!),("!.9 F ,!,/ &2$$" / ( ,!&- = A A G B48 , &,/#!.$ ,6$/& 6!. ( ,"# ', " ". ) )$ -" 2$1,1$(4 / !! :"&'$&% /&!&-% & /#+ 0"-', " ". (-) ,<=<G B4 7)/&!. /! < < A = @ 2 28

Классификация каналов по входу и выходу

< $ ($(. !.$ 7 ( !-28 D" ,!,/. &1!,/. !, % )$ & .% )$ " (.% !$ ($(. !.$&/& ,!,/ 1 .$>(&2$( ,!,/ 6(,+ ,!!.9 .% ) 2 2 ) /-" (, & % ) 2 )$2 ) /-" (,

H & ($"!.$ 7 ( !-28 D" ,!,/. &1!,/. !, % )$ & .% )$ " (.% )& ($"!.$>(&2$( ,!,/ 6(,+ ,!!.9 % ) 2 )$(, & .% ) 2 )$)$(,

A & ($"! :!$ ($(. !.$

Детерминированные и стохастические каналы

/& ,(,2$"(. ,!,/, !$ / ',9!.$ " ", 9 ,!,/ -/-$"- )$"$(2&!&( ,!!.2 ,!,/ 2 /& % "- 6. )&! ,(,2$"( ,!,/, / ',9!.9 " ", 9 ,!,/ -/-$"- " %, "&'$&2 ,!,/ 2

Каналы с постоянными или переменными параметрами

,!,/ "-!!.2& ,(,2$"(,2& D" ,!,/ " /& " ( 1 !$+, & &" " " 1 , 9 2 2$!" ($2$!& 6./ ),! % )!$+)$9 " &$/& D" / &$!$. /!-$"- " ", 9 ,!,/-/-$"-,!,/ 2 $($2$!!.2& ,(,2$"(,2&

Стационарные и нестационарные стохастические каналы

" %, "&'$&9 ,!,/ -/-$"- ",4& !,(!.2 $/& $1 " /& !, "-!!$ ($2$!& )$"$(2&!&( ,!!$% )!$ +)$9 " &$ -/-$"- ",4& !,(!.2 / ',9!.2

( 4$2 /& " /& !$",4& !,($! " & ,!,/-/-$"-!$",4& !,(!.2

Линейные и нелинейные каналы

-+# 2$3) % ) 2 & .% ) 2 ,!,/, 2,"$2,"&'$& 2 3! & ,"# +, & &2 "#0

y7t8 J x7t8			7<8
1)$ x7t8 D" % )!$ +)$9 " &$ &/& % )! 9 &1!,/ y7t8			" /& ,!,/, !, % )!$
+)$9 " &$ J x7t8 $(," ( 6 +!,',05&9		($6(,+ ,!&$&1!,/,
x7t8		y7t8
	J

& < )$/# & "$2.

+, & &2 "& " %,(, "$(, -+& 2$3) &1!,/,2& !, % )$ & .% )$ ,!,/. 2 1 " 6."# /&!$9!.2& & !$/&!$9!.2&

Линейный канал ) /$" (-$" (&!4& $( +&4&& <8 J x7t8 J x7t8 1)$ ,/-( 7'& / 8K

H8 J x< 7t8 xH 7t8 J x< 7t8 J xH 7t8

$(," ( J нелинейного,!,/, !$) /$" (-$" (&!4& $( +&4&9

Пример 1 J x7t8 k x7t8 1)$ k "-!!.9 D**&4&$!" 7 ,(,2$"( ,!,/,8 <8 J x7t8 k x7t8 7k x7t88 J x7t8

>(& x7t8 x< 7t8 xH 7t8

H8 J x< 7t8 xH 7t8 J x7t8 k x7t8 k x< 7t8 xH 7t8 k x< 7t8 k xH 7t8 J x< 7t8 J xH 7t8 /$) ,"$/#! D" " ,!,/ /&!$9!.9

Пример 2 J x7t8 k xH 7t8 >(& x7t8 x< 7t8 xH 7t8

J x< 7t8 xH 7t8 k x7t8 H k x<H 7t8 k xHH 7t8 Hkx<7t8xH 7t8 J x< 7t8 J xH 7t8 /$) ,"$/#! D" " ,!,/ !$/&!$9!.9

Импульсная характеристика линейного канала

&!$9!.$ )$"$(2&!&( ,!!.$ ,!,/. %,(, "$(&+ 0"- &2 /# ! 9 %,(, "$(& "& 9 7 8 g7t 8 " (,- -/-$"- " /& 2 ,!,/, 2 2$!" ($2$!& t !, )$/#", &2 /#

),!!.9 !,$1 % ) 2 2$!" ($2$!& t

/-*&+&'$& ($,/&+$2 9 &2 /# ! 9 %,(, "$(& "& & ) /3! . /!-"#-/ &$ g7t 8 = (& =

> /# +, & &" " ($2$!& " & . ,$2.9 $0 ,!,/ -/-$"- ,!,/ 2 $($2$!!.2& ,(,2$"(,2& /- ,!,/, "-!!.2& ,(,2$"(,2& g7t 8 g7 8 (&

/06 2 t

,!,/, "-!!.2& ,(,2$"(,2& 2 3! &+2$(&"# "L2 ),'& !, $1 % ) )&! '! 1 )$/#",:&2 /# , >(&'L2 " /& 2 ,!,/, !, D" " )$/#",:&2 /#-/-$"-

x7t8 7t8 y7t8 g7t8

,!,/

& H %$2, &+2$($!&-/&!$9! 1 ,!,/,

/& 2$" )$/#",:&2

/# , !, % ) ,!,/, ),"#

( &+ /#!.9 &1!,/ x7t8 "

" /& ,!,/, y7t8 !, D" " &1!,/ 2 3! !,9"&

2 5#0 &!"$1(,/, 0,2$/-&/& L(" &

y7t8

g7t 8 x7t 8d

7H8

/-,!,/, "-!!.2&

,(,2$"(,2&

y7t8 g7 8 x7t 8d

g7t 8 x7 8d

7A8

/#+- ($6(,+ ,!&$ F (#$ )/- y7t8 ', " "! 9 6/, "& &!"$1(,/ L(" &

"$" "$" ( &+$)$!&$

7 f 8

7G8

S y 7 f 8 K 7 f 8 Sx

1)$ Sx 7 f 8 & S y 7 f 8 ($6(,+ ,!&-F (#$ x7t8 & y7t

g7 8 N

j H f

7 8

K 7 f 8

7', " "!,-8 $($)," '!,-* ! 4&-,!,/,

>$($)," '! 0 * ! 4&0 ,!,/, 2 3! ($) ", &"# &)$ ( &+$)$!&-

j 7 f 8

7I8

K 7 f 8

1)$

2 ) /#

/$! 9

$($)," '! 9

* ! 4&& &/& ;

,!,/,

K 7 f 8

OP7K 7 f 88

7 f 8 QRSTU

,(1 2$!" 2

/$! 9

$($)," '! 9 * ! 4&& &/& F; ,!,/,

VN7K 7 f 88

Комплексные линейные каналы

Комплексный линейный канал D" ,!,/ & . ,$2.9 2 /$! 9 g7t 8

7!$,!,/&"&'$98

06 9 )$9 " &"$/#!.9 &1!,/ x7t8 2 3!

($) ", &"# &)$,!,/&"&'$1 &1!,/,

x7t8 x7t8 j x7t8

1)$ x7t8 ($6(,+ ,!&$B&/#6$(", " &1!,/, x7t8 x7t8 VN x7t8

&1!,/. !, % )$& .% )$2

/$! 1 ,!,/,-+,!. &!"$1(,/ 2 0,2$/-

y7t8

g7t 8 x7t 8d

7M8

;" 6.

$($9"&

&1!,/,2

" ,!,/&"&'$1 ($) ", /$!&- )$9 " &"$/#!.2

) "," '! +-"#$5$"$!! 0 ', "# " 2 /$! 1 ,!,/&"&'$1 &1!,/,

Основные модели линейных непрерывных каналов без помех

Каналы с постоянными параметрами

1. Идеальный канал (неискажающий канал)

&1!,/ !, .% )$D" 1 ,!,/, (,$!

s7t8 u7t + 8

7@8

1)$

u7t8 &1!,/ !, % )$ ,!,/, D**&4&$!"

$($),'& &1!,/, ,!,/$ +

+,)$(3 , ($2$!& &1!,/, ,!,/$

/-!$& ,3,05$1 ,!,/,

g7 8 7 + 8

7W8

	j H f +		7<=8
K 7 f 8 N

&1!,/ !, .% )$ &)$,/#! 1 ,!,/, " '! "#0 ) "-!! 1 D**&4&$!", " (-$" &1!,/ !, % )$

,!,/ )$9 " &"$/#!.9 7!$2 /$!.98 )$"$(2&!&( ,!!.9

/$) ,"$/#! ; &)$,/#! 1 ,!,/, ) /3!, 6."# "-!! 9 K 7 f 8 const ,

F; ) /3!, 6."# /&!$9! 9 * ! 4&$9 " ', " ". 7 f 8 Hf +

2. Канал с фазовым сдвигом

/- & ,!&- D" 9 2 )$/& !$6% )&2 $($9"& ,!,/&"&'$2 ($) ", /$!&0 &1!,/ &1!,/ !, .% )$ -+,! &1!,/ 2 !, % )$/$) 05$9 +, & &2 "#0

	s7t8 N j u7t8					7<<8
&/&						7<H8
&/&	s7t8 VN s7t8	u7t8 SXY7 8 u7t8 YZ[7 8				7<H8
1)$	s7t8 s7t8 js7t8 ,!,/&"&'$ $	($) ", /$!&$&1!,/, s7t8 !, .% )$				,!,/,
u7t8	u7t8 ju7t8 ,!,/&"&'$ $ ($) ", /$!&$&1!,/, u7t8 !, % )$,!,/, u7t8 & s7t8
($6(,+ ,!&$B&/#6$(", " u7t8 & s7t8 $/&'&!, *,+ 1 ) &1, &1!,/, ,!,/$
	/-,!,/, *,+ .2 ) &1 2
	g7 8 N j 7 8					7<A8
			j			7<G8
	K 7 f 8 N					7<G8
	,!,/ 2 /$!.9 )$"$(2&!&( ,!!.9			j =t
				j =t	*,+ .9 ) &1 2 3$" 6."# .+ ,!
	>(& $($),'$+ / !.% &1!,/ u7t8 A7t8 N				*,+ .9 ) &1 2 3$" 6."# .+ ,!
!$6 /#E 9 ($2$!! 9 +,)$(3 9 &1!,/, 1),				<? f > /# 2		/$!,-

1&6,05,- A7t8 2$)/$!! 2$!-$"-($2$!& "

s7t8 u7t 8 A7t 8 N j = 7t 8 A7t8 N j =t N j = u7t8 N j 1)$ = *,+ .9 ) &1

	3. Однолучевой канал с постоянными параметрами
	\", 2 )$/# ($) ", /-$" 6 9 6]$)&!$!&$ $( .% ) % 2 )$/$9
	&1!,/ !, .% )$)! / '$1 ,!,/, (,$!
	s7t8 u7t + 8	7< 8
&/&	s7t8 VN s7t8 u7t + 8 SXY7 8 u7t + 8 YZ[7 8	7<I8
1)$	N j 2 /$!.9 D**&4&$!" $($),'& &1!,/, ,!,/$
	,!,/ !,+. ,0" )! / '$.2 ,!,/ 2 " 2 '" " ' (&L2,	(&% )&" )!,

+,)$(3,!!,- &-&1!,/, 6 "$!!.2 D**&4&$!" 2 $($),'& /-D" 9 2 )$/&

g7 8 7 + 8 K 7 f 8 N j N j H f +

,!,/ 2 /$!.9 )$"$(2&!&( ,!!.9

Каналы с переменными параметрами 4. Канал с частотным сдвигом спектра сигнала

&1!,/ !, .% )$,!,/, ', " "!.2 ) &1 2 (,$!

7<M8

7<@8

s7t8 u7t8 N j t		7<W8
s7t8 VN s7t8 u7t8 SXY7 t8 u7t8YZ[7 t8		7H=8
1)$ u7t8 & s7t8 2 /$!.$,!,/&"&'$&$&1!,/. !, % )$& .% )$,!,/,
/-,!,/, ', " "!.2 ) &1 2
g7t 8 7 8 N j t		7H<8
	j t	7HH8
K 7 f t8 N

,!,/ 2 /$!.9 )$"$(2&!&( ,!!.9 &1!,/. 2 1 " / '&"# ) /!&"$/#!.9 ', " "!.9 ) &1 (& " / !$!&& ', " "

1$!$(," ( $($),"'& , & (&L2!& , " ! 2&!,/#!.% +!,'$!&9 &/& (& ) &3$!&& $($),"'& , & (&L2!& , "! &"$/#! )( 1 )( 1, ( "#0 v ($+ /#","$ '$1

+!& ,$" ) /$( &9 ', " "!.9 ) &1 fd f=v ? c

5. Однолучевой канал с замираниями сигнала

6 /#E&! "$ ($,/#!.% ,!,/,% 2 /$!.9 D**&4&$!" $($),'& N j 2$!-$"- ($2$!& > D" 2 6 65$!&$2 2 )$/& )! / '$1 ,!,/, 2 3$" / 3&"# 2 )$/# )! / '$1 ,!,/, +,2&(,!&-2& )/-" ( 9

s7t8 7t8 u7t + 8			7HA8
s7t8 VN 7t8 u7t + 8	7t8	u7t + 8 SXY7 7t88 u7t + 8 YZ[7 7t88	7HG8

1)$ 7t8	7t8	N j 7t 8 2$!-05&9- ($2$!& 2 /$!.9 D**&4&$!"			$($),'& ,!,/,
+ +,)$(3 , &1!,/, ,!,/$ u7t8 & s7t8			2 /$!.$,!,/&"&'$&$&1!,/. !, % )$
& .% )$,!,/,
/-)! / '$1 ,!,/, +,2&(,!&-2& & $($)," '!,-* ! 4&-+, &-" " ) %
$($2$!!.%		g7t 8 7t8 7 + 8			7H 8

				j H f +	7HI8
		K 7 f t8 7t8 N
				)$"$(2&!&( ,!!,- * ! 4&- ($2$!& "
/& D**&4&$!" $($),'& ,!,/, 7t8
				/ ',9!.9 ( 4$ "	,!,/ -/-$"-
,!,/ )$"$(2&!&( ,!!.9 /& 7t8
" %, "&'$&2
+2$!$!&$ ($2$!& D**&4&$!",
				$($),'& ,!,/, 7t8 .+. ,$" +,2&(,!&$

&1!,/, ($,/#!.% ,!,/,% !, (&2$( (,)& ,!,/,% 7t8 -/-$"- / ',9! 9 * ! 4&$9 ($2$!& &/& / ',9!.2 ( 4$2 F&+&'$,- ($), " ( 9 (, ( "(,!-$"- &1!,/ /,6/-$" & (,$& ,$"$1 , ($2$!& ", & ( "(,! "$/& (,$-!&$($2$!& !$6 /#E$ " 2 3! '&","# '" " ' (&L2, (,+/&'!.2 "(,$" (&-2 &/& "-2 (&% )&" ^ '_ "-5&9 &+ 6$!$'! 1 '& /, +,)$(3,!!.% &9 $($),!! 1

&1!,/, &2$05&% (,+/&'!.$/ ',9!.$D**&4&$!". $($),'& & +,)$(3 &

s7t8 k 7t8 u7t +k 7t88

7HM8

/& $($), ,$2.9

&1!,/

+ / !.9 " $1 2 3!

($) ", &"#

,+&1,(2 !&'$9 * (2$2$)/$!! 2$!-05$9-,2

/&" ) 9 & *,+ 9

j =t

7H@8

u7t8 A7t8 N

1), (& +k 7t8

+k 7t8

+ +k

7t8 & / && '" +k <? fS

+k 7t8

7t88 N

j = 7t + + k 7t 88

8 N

j =

7t + 8

j = + k

7t 8

u7t +

8 N

j = +k 7t 8

u7t +k 7t88 A7t + +k

A7t +

/$) ,"$/#!

k 7t8 N

j = + k 7t 8

8 7t8 u7t + 8

7HW8

s7t8

u7t +

1)$ 7t8 2

/$!.9 D**&4&$!"

$($),'& ,!,/,

k 7t8 N

j = + k 7t 8

k 7t8 SXY7= +k 7t88 j k 7t8 YZ[7= +k 7t88

7A=8

7t8

7t8 c 7t8 j s

7t8 ` 7t8 ` N j 7t 8

7A<8

1)$ c 7t8 & s 7t8 ,)(," (!.$ 2

!$!". 7t8 " (.$ "-" &+ 22. 6$!$'!

6 /#E 1 '& /, /,6 (($/&( ,!!.% / ',9!.%$/&'&! 1(,!&'$!!.2& )& $( &-2& 1/, ! 4$!"(,/#! 9 ($)$/#! 9 "$($2$ "$(&& $(-"! "$9 2 3! '&","# '"

,)(," (!.$2 !$!". &2$0" ! (2,/#!$&/& 1,$(, ($)$/$!&$ $(-"! "& W

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.201810.04 Mб48Книга ЭВМ.docx
#
10.06.2015222.21 Кб22ком. мен. лекции.doc
#
25.09.2019279.55 Кб19Команды общего назначения.doc
#
17.04.2019147.46 Кб18Компенс ст рег.doc
#
29.03.20161.46 Mб65Конспект Введение в спец. .pdf
#
10.06.20151.85 Mб112Конспект лекции по ТЭС.pdf
#
21.12.20182.42 Mб60Конспект лекций И-М.doc
#
10.06.2015900.61 Кб179Конспект лекций по дисц.ОИК. Часть 4..doc
#
29.03.20163.66 Mб322Конспект лекций по КГ.doc
#
10.06.20151.09 Mб76Конспект лекций по рекламе в ком. процессе..doc
#
10.06.20151.65 Mб32Конспект лекций по УК.docx