Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект лекции по ТЭС

.pdf

Скачиваний:

112

Добавлен:

10.06.2015

Размер:

1.85 Mб

Скачать

☆

1 / 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Курс лекций по теории электрической связи

(ТЭС)

Часть 1. Часть 2.

Автор: к.т.н.,
доц. кафедры ТОРС	Петров О.А.

Самара, 2008 г.

ЛЕКЦИОННЫЙ КУРС ПО ТЭС

ЛЕКЦИЯ 1. ЧАСТЬ 1 ВВЕДЕНИЕ. СИСТЕМЫ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ. ОСНОВНЫЕ ЗАДАЧИ,

ПОНЯТИЯ И МЕТОДЫ ТЕОРИИ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ

Предмет и круг задач теории электрической связи (ТЭС). Понятия информации, сообщения, сигнала, канала и системы связи. Структурные схемы систем передачи непрерывных и дискретных сообщений. Основные преобразования сигналов в системах электрической связи. Сущность и цели операций кодирования, модуляции, декодирования и демодуляции. Основные характеристики систем связи.

Список литературы

1.Зюко А.Г., Кловский Д.Д., Назаров М.В, Финк Л.М. Теория передачи сигналов. – М.: Радио и связь, 1986 г.

2.Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. Теория электрической связи / Под ред. Д.Д. Кловского. – М.: Радио и связь, 1998 г.

3.Кловский Д.Д. Теория передачи сигналов. – М.: Связь, 1973.

4.Кловский Д.Д., Шилкин В.А. Теория электрической связи. – Сборник задач и упражнений. – М.: Радио и связь, 1990.

5.Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах. – М.: Связь, 1978.

6.Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Радио и связь, 1988.

Теория электрической связи (ТЭС) включает в себя следующие разделы:

1.Теория сигналов и случайных процессов.

2.Теория модуляции и детектирования.

3.Статистическая теория связи.

4.Теория информации.

5.Теория кодирования.

Определения Информация – совокупность сведений о событии или явлении. Её можно передавать и хранить в виде сообщений.

Сообщение – совокупность знаков и символов, отображающих информацию. Сообщения могут быть непрерывными (в виде непрерывных функций) и дискретными (в виде дискретной последовательности символов (букв и знаков)).

Сигнал – физический процесс, используемый для передачи сообщений. Математически сигнал представляется в виде функции времени. Для него можно задать длительность Tc ,

полосу частот шириной Fc и динамический диапазон Dc Pmax / Pmin , где Pmax и Pmin – максимальная и минимальная мощности сигнала. Произведение этих трёх параметров определяет объём сигнала.

Система связи – совокупность технических средств, обеспечивающих передачу сообщений от источника к получателю (потребителю).

Канал – совокупность технических средств и физическая среда, которые используются для передачи сигналов между двумя точками системы связи.

Помеха – любое воздействие на сигнал, которое его искажает и ухудшает верность воспроизведения сообщений в приёмнике. Помехи по физической природе можно разделить на атмосферные, индустриальные, межканальные, внутренние шумы аппаратуры и др. По характеру воздействия их разделяют на узкополосные, импульсные и флуктуационные.

Физическая система – совокупность физических объектов, между которыми существуют определённые взаимодействия. Каждый объект физической системы имеет хотя бы один вход и один выход. Связь между входом и выходом задаётся системным оператором T ,

связывающий входное воздействие uвх (t) и выходной отклик или реакцию системы uвых (t) :

uвых (t) T uвх (t) .

Система связи является физической системой.

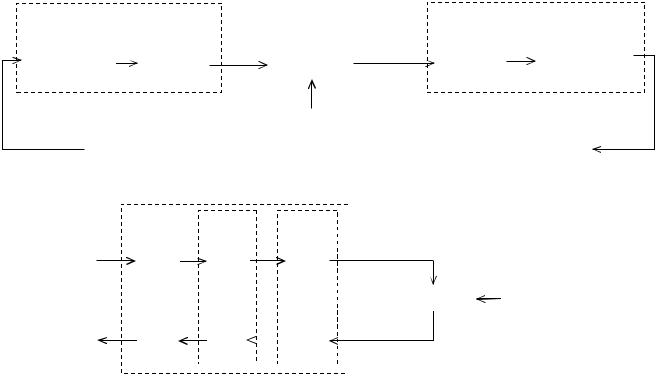
На рисунках 1 и 2 представлены структурные схемы одноканальной аналоговой и цифровой систем связи.

Передатчик

Приёмник

b(t)

u(t)

z(t) s(t) n(t)

b(t)

Преобразователь

Модулятор

Демодуля-

Преобразователь

сообщений в

Линия связи

тор

сигнала в

сигнал

сообщение

Источник

a(t)

помех

aˆ

(t)

Источник

Получатель

сообщений

Рис. 1. Структурная схема одноканальной аналоговой системы связи.

Кодек

Модем

a(t)

ui (t)

Модуля-

ИС

АЦП

Кодер

тор

b(t)

(цифровой)

Источник

Линия связи

помех

aˆi

aˆ(t)

z(t) si (t) n(t)

ПС

ЦАП

Декодер

Демоду-

лятор

(цифровой)

b(t)

Рис. 2. Структурная схема цифровой системы связи.

Объединение источника непрерывных сообщений с АЦП можно рассматривать как источник дискретных сообщений. Элементами дискретных сообщений являются символы ai .

При передаче дискретных сообщений каждый элемент сообщения кодируется в последовательность кодовых символов, которую называют кодовой комбинацией.

Код – совокупность всевозможных кодовых комбинаций.

Кодирование – преобразование сообщения в последовательность кодовых символов. Декодирование – процедура обратная кодированию, восстанавливает из принятых кодовых символов переданное сообщение.

Кодовые символы выбираются из некоторого алфавита. Общее число символов в алфавите называют объёмом алфавита или основанием кода.

Если кодовые символы выбираются из алфавита, состоящего из символов 0 и 1, то код называют двоичным кодом или кодом по основанию 2. Из-за своей простоты двоичные коды наиболее часто используются для кодирования сообщений.

		a0 26					a1 21					символы передаваемого
		b(26)					b(21)					сообщения
		b(26)	(11010)		2		b(21)	(10101)		2		кодовые комбинации
		0			2		1			2
br	1	1	0	1	0	1	0	1	0		1	первичный
b(t)												модулирующий сигнал
	T											t
u(t)	T											сигнал на выходе
u(t)												модулятора
												t
z(t)												сигнал на входе
z(t)												приёмника

сигнал на выходе

ˆ демодулятора b(t)

ˆ	1	1		0	0	0	1	0	1	0	1
br	1	1		0	0	0	1	0	1	0	1
		ˆ (26)	(11000)2					ˆ (21)	(10101)2		принятые кодовые
		b0	(11000)2					b1	(10101)2		комбинации
			aˆ0	24					aˆ1 21		комбинации
			aˆ0	24					aˆ1 21		принятые символы
											сообщения
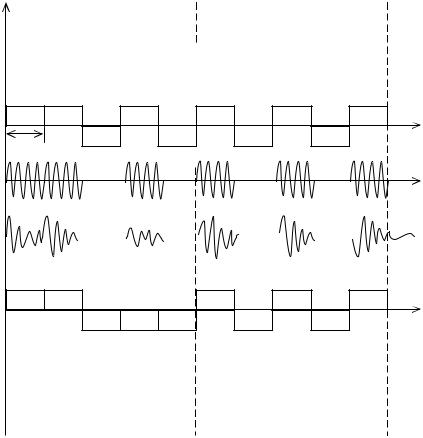
		Рис. 3.		Дискретные сообщения и сигналы в цифровой системе связи.

Кодирование может быть примитивным, помехоустойчивым и экономным.

При примитивном кодировании осуществляется преобразование кода. Оно используется для согласования входов и выходов различных устройств систем связи. Например, если система связи предназначена для передачи двоичных символов, то для передачи текста необходимо каждую букву заменить последовательностью двоичных символов, т.е. закодировать его кодовыми комбинациями двоичного примитивного кода.

При помехоустойчивом кодировании к кодовым комбинациям примитивного кода добавляют специальные символы, которые называют проверочными символами. Проверочные символы дают возможность обнаружить и исправить ошибки в кодовых комбинациях, поэтому помехоустойчивое кодирование называют также кодированием, исправляющим ошибки.

При экономном кодировании из сообщений устраняется избыточность, обусловленная часто повторяющимися символами и зависимостью символов в сообщениях. В результате устранения избыточности сообщения становятся более короткими, т.е. происходит сжатие сообщений. Сжатие бывает без потери информации и с потерей информации. В последнем случае информация восстанавливается не полностью, а приближённо, с некоторой заданной точностью, но при этом достигается большая степень сжатия.

Модуляция – это изменение одного или нескольких параметров несущего сигнала (переносчика, несущей) по закону модулирующего (первичного) сигнала. Если в качестве переносчика выбрать гармоническое колебание, то модуляция может быть амплитудной (АМ), частотной (ЧМ) и фазовой (ФМ).

Если в качестве переносчика выбрать периодическую последовательность импульсов, параметрами которых являются амплитуда, ширина и временное положение импульса в периоде, то в зависимости от выбранного параметра модуляция может быть амплитудноимпульсной (АИМ), широтно-импульсной (ШИМ) и время-импульсной (ВИМ).

Устройство, осуществляющее модуляцию, называют модулятором. В зависимости от вида модулирующего сигнала модуляторы бывают аналоговыми и цифровыми. При цифровой передаче в качестве модулирующего колебания выступает первичный цифровой сигнал. Демодуляция – процедура обратная модуляции, процесс восстановления из принятого сигнала модулирующего сигнала.

В цифровых системах связи модулятор и демодулятор объединяют в одно устройство – модем, а кодер и декодер – в кодек.

Сигнал на входе приёмника можно представить в виде суммы

z(t) s(t) n(t) ,	(1)
где s(t) – полезный сигнал на входе приёмника, n(t)	– аддитивная помеха.

Сигнал s(t) является некоторым функциональным преобразованием сигнала u(t) :

s(t) T[u(t)].	(2)
Примером функционального преобразования может служить преобразование вида
s(t) T[u(t)] (t) u(t) ,	(3)
где (t) – мультипликативная помеха (меняющийся во времени коэффициент	передачи
канала).
В результате искажений и воздействия помех наблюдаемый сигнал z(t)	на входе

приёмника может существенно отличаться от переданного. Задачей приёмного устройства является принятие решения о том, какое сообщение было передано путём анализа принятого сигнала с учётом всех сведений об источнике сообщений, способов кодирования, модуляции и свойств канала. Поиск решения осуществляется по заданному правилу.

Одной из основных задач теории связи является отыскание такого правила принятия решения, при котором решение о переданном сообщении было бы наиболее достоверным.

Основные характеристики систем связи Помехоустойчивость системы связи – способность системы связи противостоять

вредному воздействию искажений и помех.

При передаче непрерывных сообщений помехоустойчивость обычно оценивается средним квадратом ошибки, а при передаче дискретных сообщений – вероятностью ошибки символа принятого сообщения.

Помехоустойчивость зависит от различимости передаваемых сигналов, от отношения сигнал-помеха и выбранного способа приёма. Чем сильнее сигналы на передаче отличаются друг от друга (большая различимость сигналов) и чем больше отношение сигнал–помеха, тем выше будет помехоустойчивость.

Другим показателем является скорость передачи информации Rи . Количество

информации обычно измеряется в битах, поэтому скорость передачи информации измеряется числом бит в единицу времени.

Бит – это количество информации, содержащееся в двоичном символе, принимающем с равной вероятностью значения 0 и 1. В данном случае бит не следует путать с двоичным символом. Максимальное количество информации, которое может содержаться в одном двоичном символе равно одному биту.

Пропускная способность C канала связи – это максимальная скорость передачи информации по каналу. Если Rи C , то можно построить такую систему связи, в которой информация от источника будет полностью доходить до получателя, т.е. все сообщения будут приняты без ошибок. Если Rи C , то в канале связи возникнут потери информации и до получателя она дойдёт не полностью, т.е. сообщения будут приняты с ошибками.

ЛЕКЦИЯ 2

Поля и векторные пространства. Определения нормы, расстояния и скалярного произведения в пространствах Евклида, Гильберта и Хэмминга, их физический смысл. Базисы и ортогональные разложения в пространстве сигналов (обобщённые ряды Фурье).

Числовое поле F

Числовое поле F(q) a0 , a1 ,..., aq 1 – это совокупность из q элементов (чисел), для

которых однозначно заданы операции сложения (+), вычитания (–), умножения ( ) и деления

(÷).

Элементы любого поля должны удовлетворять следующим условиям:

существует единственный

нулевой

элемент поля

0 F

такой,

что

0 a a

(нейтральный по сложению) и 0 a 0 , где a F ;

1 a a

существует

единственный

единичный

элемент поля

1 F

такой,

что

(нейтральный по умножению), где a F ;

2) если ai , a j F , то

a j

ak F (свойство замкнутости по сложению) и

a j ar

F (свойство замкнутости по умножению);

ai a j a j

ai ,

ai a j

a j

(коммутативность);

(ai

a j ) ak ai (a j

ak ) ,

(ai a j ) ak

ai (a j ak )

(ассоциативность);

(ai

a j ) ak

ai ak

a j ak

(дистрибутивность);

6) обратный элемент по сложению (ai ) F находится из уравнения (ai ) ai 0 ;

обратный элемент по умножению ai 1 F находится из уравнения ai 1 ai 1.

Примеры полей: – множество вещественных чисел, – множество комплексных чисел, – множество рациональных чисел. Эти поля содержат бесконечное число элементов ( q ). Множество натуральных и целых чисел полями не являются.

Поле и расширение поля

Если некоторое поле F2 содержит в своём составе элементы другого поля F1 , причём все свойства элементов этого поля сохраняются в F2 , то F1 называют основным полем, а F2

– расширенным полем или расширением поля F1 . Например, поле комплексных чисел является расширением поля действительных чисел.

Поле комплексных чисел

Комплексное число – это число, представленное в виде

где a Re[c]

c a jb ,

a, b ,

b Im[c]

– действительная

часть комплексного числа

–

мнимая часть

комплексного числа,

– мнимая единица.

Формула Эйлера: e j cos( ) j sin( ) .

e j ,

Показательная

форма комплексного числа: c

где

a2 b2 –

модуль

комплексного числа, arg(c) atan2(a,b) – аргумент комплексного числа.

e j .

Комплексно-сопряжённое число c a jb

Свойства модуля:

;

cos x

y .

x y

2 c c ;

2 Re x y

Поле с конечным числом элементов

Существуют поля, содержащие конечное число элементов ( q ). Такие поля называются полями Галуа и обозначаются GF(q) . Для существования поля Галуа число его

элементов должно быть равным q pm , где p

– простое число, m 0 – целое число.

Если m 1, то поле

Галуа является

простым.

простом

поле

арифметические

операции выполняются по модулю простого числа p : ak

(ai a j ) mod p , ar

(ai a j ) mod p ,

где a mod p означает остаток от деления a на p (не путать с абсолютной величиной).

Свойства операции mod

Векторное пространство

Числовое поле

(a b) mod c ((a mod c) (b mod c)) mod c

;

(a b) mod c ((a mod c) (b mod c)) mod c ;

(a b) mod(c b) b (a mod c) .

, ,

GF(q)

n , n , GFn (q)

Отметим, что если

p будет составным

числом,

то

операция умножения

будет

неоднозначной и, следовательно, поле Галуа с таким числом элементов не существует.

Доказательство.	Если p p1 p2 , то при ai		p1 GF(q)	и a j p2 GF(q)
ai a j mod p p1 p2	mod p 0 , что возможно, если либо	ai	0 , либо	a j 0 . Т.к. ai p1 0 и

a j p2 0 , то в поле существует два нулевых элемента, что противоречит условию 1 для

элементов поля.
	Пример: GF(2) 0,1 – поле Галуа с наименьшим числом элементов.
	Если m 1, то поле GF( pm ) является расширением простого поля GF( p) . Элементы
поля	GF( pm ) можно рассматривать как	многочлены	a(x) a	m 1	xm 1 ... a x a		0	степени
	с коэффициентами из GF( p) .			m 1	1		0
m 1	с коэффициентами из GF( p) .	Для задания	операций		умножения	и		деления

используется неприводимый многочлен pm (x) степени m . Неприводимый многочлен – это

многочлен, который нельзя разложить на произведение многочленов меньшей степени. При сложении (вычитании) многочленов коэффициенты при одинаковых степенях складываются (вычитаются). Умножение и деление элементов (многочленов) расширенного поля выполняются по модулю этого неприводимого многочлена: ak (x) ai (x) a j (x) mod pm (x) .

Векторное пространство Fn

Набор (a0 , a1,..., an 1 ) из n элементов называют n-мерным вектором и обозначают a . Элементы вектора также называют координатами.

Векторное пространство Fn – это совокупность n-мерных векторов с элементами из поля F , для которых заданы операции умножение на скаляр и сложение векторов:

1)a a0 , a1 ,..., an 1 Fn , – скаляр (число);

2)a b a0 , a1 ,..., an 1 b0 , b1 ,..., bn 1 a0 b0 , a1 b1 ,..., an 1 bn 1 Fn .

Нулевой вектор 0 Fn – это вектор, состоящий из нулевых элементов поля F .

Если векторное пространство дополнить операцией умножения векторов, то векторное пространство становится расширенным полем.

Пространство Евклида ( n или n )

Если в качестве элементов векторов выбраны элементы поля действительных чисел или поля комплексных чисел , то векторное пространство, в этом случае, называют

евклидовым пространством и обозначают n или n .

Евклидово пространство является нормированным и метрическим пространством.

Норма – это длина вектора:

n 1

| ai |2 .

(4)

Свойства нормы:

i 0

0 ;

;

a b

Метрика – это расстояние между двумя векторами, которое находится как норма

разности векторов:

n 1

d (a, b)

a b

| ai

bi |2

(5)

Свойства метрики:

i 0

1) d (a, b) 0

и d (a, b) 0 , если a b ;

d (a,b) d (b,a) ;

3) d (a,b) d (a, z) d (b, z) (неравенство треугольника).

Скалярное произведение – это проекция одного вектора на другой в пространстве векторов:

n 1

a,b ai

b i

cos( ) ,

(6)

i 0

где – угол между векторами.

Если (a,b) 0 , то векторы a и b называют ортогональными векторами.

Если (a, b)

, то векторы a и b называют коллинеарными векторами.

Неравенство Буняковского–Шварца

a,b

(7)

Знак равенства выполняется при b a , где

– скаляр.

Пространство Гильберта

Если n , то конечномерное пространство Евклида становится бесконечномерным пространством Гильберта L2 (T / 2,T / 2) , элементами которого являются непрерывные

функции аргумента t , интегрируемые в квадрате на интервале t T / 2;T / 2 . Норма в Гильбертовом пространстве равна

T / 2

dt .

(8)

x(t) x(t)dt

x(t)

T / 2

Метрика в пространстве Гильберта равна

T / 2

2 dt .

d (x, y)

x y

x(t) y(t)

(9)

T / 2

Скалярное произведение определяется выражением

T / 2

(x, y)

(10)

x(t) y(t)dt .

Пространство Хэмминга

T / 2

GF(q) , то

Если в качестве элементов

векторов выбраны

элементы поля Галуа

векторное пространство, в этом случае, становится пространством Хэмминга.

В качестве нормы используется вес вектора (x) , который равен числу ненулевых

элементов вектора.

В качестве метрики используется расстояние по Хэммингу между векторами, которое равно d (x, y) (x y) .

Линейная независимость векторов

Совокупность векторов

, a ,..., a

n 1

является

линейно-независимой,

если их

линейная комбинация

n 1

0a0 1a1

... n 1an 1 0

или

iai 0

(11)

i 0

для любых i F , одновременно не равных нулю. Т.е. ни один из векторов ai

не может быть

представлен в виде линейной комбинации остальных.

n 1

Иначе, если iai 0 ,

то

любой из векторов

можно выразить

виде

линейной

i 0

комбинации остальных векторов:

a0 (1 / 0 )a1 (2

/ 0 )a2

... (n 1

/ 0 )an 1 .

(12)

Базис векторного пространства

Совокупность из n линейно-независимых векторов a

, a ,..., a

n 1

называют базисом

векторного пространства, потому что любой вектор пространства можно выразить с помощью их линейной комбинации, т.е. если b Fn , то

n 1
b ciai .	(13)
i 0	(3, 2,1) . Выразим вектор b (2, 3,1) :
Пример: n 3 , a0 (1, 2,3) , a1 (2,1,3) и a2	(3, 2,1) . Выразим вектор b (2, 3,1) :

b (2, 3,1) 1 a0 ( 1) a1 1 a2 .

Ортогональный базис векторного пространства

В любом векторном пространстве конечномерном или бесконечномерном можно

выбрать линейно-независимые ортонормированные векторы ψi такие, что
	1, i j,		(14)
	(ψi , ψ j ) i j 0, i j,		(14)
где k	– символ Кронекера. Пример: n 3 , ψ0 (1, 0, 0) ,	ψ1 (0,1, 0) и ψ2	(0, 0,1) .

Ортонормированные векторы можно использовать в качестве ортогонального базиса, т.е. рассматривать их как оси новой системы координат.

Переход от линейно-независимых векторов к ортонормированным векторам можно осуществить с помощью ортогонализации Грамма–Шмидта.

Обобщённый ряд Фурье или разложение вектора по ортонормированному базису

Обобщённый ряд Фурье – это представление любого вектора x в виде линейной комбинации ортонормированных векторов ψi :

	n 1
	x ck ψk ,	(15)
	k 0
где	ck (x, ψk )	(16)

–коэффициенты обобщённого ряда Фурье.

Впространстве Гильберта обобщённый ряд Фурье будет следующим


	x(t) ck k (t) ,		(17)
	k 0
	T / 2	*
где	ck x, ψk	x(t) k (t)dt .	(18)

T / 2

Разложение в обобщённый ряд Фурье позволяет характеризовать сигналы совокупностью коэффициентов ck .

ЛЕКЦИЯ 3

МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ХАРАКТЕРИСТИКИ СООБЩЕНИЙ, СИГНАЛОВ И ПОМЕХ

Классификация сообщений, сигналов и помех. Временное и спектральное представления сигналов в системах связи. Спектры периодических и непериодических сигналов. Ряд Фурье, интеграл Фурье и преобразования Фурье. Примеры спектров различных видов сигналов и сообщений. Энергия и средняя мощность сигналов. Равенство Парсеваля.

Классификация сообщений, сигналов и помех

Сообщения, сигналы и помехи в ТЭС математически представляют некоторой функцией x(t) . Функция x(t) – это закон, согласно которому каждому значению

независимой переменной t ставится в соответствие единственное значение x . Функция может быть задана: 1) аналитически – в виде математической формулы, например, x(t) 10cos(2 1000t / 4) – гармоническое колебание, где 10 – амплитуда, 1000 – частота,

/ 4 – начальная фаза; 2) таблично; 3) графически. Если сигнал описывает изменение во времени напряжения на некотором сопротивлении, то функция, описывающая такой сигнал, будет иметь размерность вольт.

Детерминированные и случайные сигналы

Детерминированные сигналы – это сигналы, мгновенные значения которых известны достоверно в любой момент времени. Если мгновенные значения сигнала случайные, то такой сигнал является случайным. Случайные сигналы называют ещё случайными процессами. Примером детерминированного сигнала является гармоническое колебание из предыдущего примера.

Периодические и непериодические сигналы

Сигнал называют периодическим по времени, если существует такое постоянное

T0 0 , для которого
x(t T0 ) x(t)	( t ) .	(19)

Наименьшее значение T0 , для которого выполняется это условие, называют периодом сигнала T . Сигналы, не удовлетворяющие условию (19), называют непериодическими.

Дискретные и непрерывные сигналы

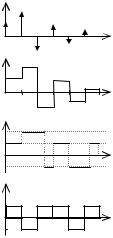
Сигнал называют дискретным по времени, если он принимает свои значения только в заданные моменты (рис.4,а) или интервалы времени (рис.4,б).

Сигнал называют дискретным или квантованным по уровню

(по напряжению), если он принимает свои значения из некоторого заданного конечного множества уровней (рис.4,в).

Иначе, если сигнал непрерывный и по времени, и по уровню, то такой сигнал называют аналоговым сигналом.

Цифровой сигнал

Цифровой сигнал – это сигнал, используемый для передачи потока цифровых данных, обычно двоичных символов или бит. Цифровой сигнал дискретный по времени и по уровню (рис.4,г).

x(t)

x(t) a)

б)

x(t)

в)

1 0 1 1 0 1

г) Рис. 4.

1 / 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.201810.04 Mб48Книга ЭВМ.docx
#
10.06.2015222.21 Кб22ком. мен. лекции.doc
#
25.09.2019279.55 Кб19Команды общего назначения.doc
#
17.04.2019147.46 Кб18Компенс ст рег.doc
#
29.03.20161.46 Mб65Конспект Введение в спец. .pdf
#
10.06.20151.85 Mб112Конспект лекции по ТЭС.pdf
#
21.12.20182.42 Mб61Конспект лекций И-М.doc
#
10.06.2015900.61 Кб179Конспект лекций по дисц.ОИК. Часть 4..doc
#
29.03.20163.66 Mб322Конспект лекций по КГ.doc
#
10.06.20151.09 Mб76Конспект лекций по рекламе в ком. процессе..doc
#
10.06.20151.65 Mб32Конспект лекций по УК.docx