
Конспект лекции по ТЭС
.pdf
Алгоритм экономного кодирования кодом Хаффмана:
1. Символы источника выписываются в порядке убывания их вероятностей. Если число символов источника M m не кратно m , то алфавит дополняют до кратности новыми символами с вероятностью равной 0.
2.Выбираются m символов с наименьшими вероятностями. От каждого из них вправо рисуются ветви, на которых произвольно отмечаются кодовые символы от 0 до
m1 .
3.Эти символы объединяются в один укрупнённый символ с вероятностью равной их сумме вероятностей.
4.Повторяем п.2 и 3, пока не закончатся все символы.
5.Справа налево по дереву выписываются последовательности кодовых символов, соответствующие исходным символам источника.
6.Кодирование исходного сообщения полученным кодом.
Пример. Для текста на русском языке H (A) 1,5 бит/символ. Для удобства примем, что объём алфавита M 32 буквы. Закодируем каждый символ источника (длина k 1 ) примитивным двоичным ( m 2 ) кодом. Для этого длина кодовых комбинаций должна быть равна log2 M log2 32 5 дв.символов. Тогда n / k 5 код.символов/символ источника.
Согласно теореме кодирования Шеннона для дискретного источника существует оптимальный двоичный код, с помощью которого каждую букву источника можно
закодировать в среднем |
n |
|
H (A) |
|
1,5 |
1,5 дв.символов/символ источника. |
k |
log2 m |
|
||||
|
|
1 |
|
|||
Следовательно, закодированный таким экономным кодом текст будет в 5/1,5 3,3 раза короче, чем при примитивном кодировании.
120
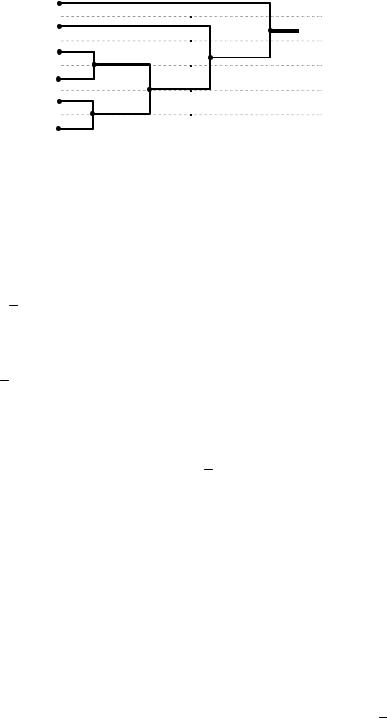
Пример 1. Имеется стационарный источник без памяти с алфавитом из M 6 символов. Для кодирования используем код Хаффмана с параметрами: длина информационных (кодируемых) последовательностей источника k 1 (кодируются символы), основание кода m 2 (кодовые символы двоичные).
Исходные данные и построение кодового дерева представлены в таблице 1.
Таблица 1. Таблица кодирования двоичным кодом Хаффмана.
|
i |
|
ai A |
|
P(ai ) |
|
|
|
|
|
Кодовое дерево |
|
ci |
ni |
|
|
0 |
|
a0 |
|
0,4 |
|
|
|
|
|
|
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
0 |
|
1 |
|||||
|
1 |
|
a1 |
|
0,3 |
|
0 |
|
|
|
|
10 |
2 |
||
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
a2 |
|
0,1 |
|
0,18 |
|
0 |
0,6 |
1 |
|
1100 |
4 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0,3 1 |
|
|
|
|
|
3 |
|
a3 |
|
0,08 |
|
1 |
|
|
|
|
|
1101 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
4 |
|
a4 |
|
0,07 |
|
0,12 |
|
1 |
|
|
|
1110 |
4 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
5 |
|
a5 |
|
0,05 |
|
1 |
|
|
|
|
|
|
1111 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рассчитаем энтропию и избыточность источника: |
|
|
|
|
|||||||||||
|
|
|
|
M 1 |
|
1 |
|
|
|
|
|
|
|
||
|
|
H (A) P(ai ) log2 |
|
|
|
2,158 [бит/символ источника]. |
|
||||||||
|
|
P(a ) |
|
||||||||||||
|
|
|
|
i 0 |
|
i |
|
|
|
|
|
|
|
||
A |
1 |
H (A) |
1 |
2,158 |
0,165 16,5% . |
log2 M |
|
||||
|
|
2,585 |
|
||
Средняя длина полученных после кодирования кодовых комбинаций равна
|
|
|
|
|
M 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
P(ai )ni |
2, 2 [кодовых символа]. |
||||||||||||||||||
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассчитаем энтропию и избыточность кодера: |
|
|
|
|
|
|
|
||||||||||||||||
H (C) |
k |
H (A) |
1 |
2,158 0,981 [бит/кодовый символ]. |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
n |
|
|
|
2, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
C |
1 |
H (C) |
1 |
0,981 |
0, 019 1,9% . |
||||||||||||||||
|
|
log2 m |
|
|
|||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
k log2 |
M |
|
||||||||||||
Скорость кода или коэффициент сжатия Rc |
1,17 раза. |
||||||||||||||||||||||
|
n |
|
log2 m |
|
|||||||||||||||||||
Эффективность кодирования этого кода равна |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
C |
1 |
0, 019 |
0,88 88% . |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
C |
|
A |
0,165 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Существует ещё 12% остаточной избыточности, которую можно устранить, если для кодирования, согласно теореме Шеннона, выбрать большие значения k . В следующем примере будет рассмотрен случай, когда для повышения эффективности кодирования делается переход от использования комбинаций длины k 1 к k 2 .
Примечание. Если бы для кодирования использовался двоичный код, то минимальная длина кодовых комбинаций была бы равной n log2 M 3 (двоичных) кодовых символа.
Отметим, что этот код не примитивный, а избыточный или помехоустойчивый, поскольку Nк.к 5 Nобщ mn 23 8 . Использование кода Хаффмана для кодирования символов этого двоичного кода позволило бы сжимать сообщения с коэффициентом Rc n / n 3 / 2, 2 1,36 раза. Это значение превышает Rc 1,17 , потому что данный двоичный код внёс
дополнительную избыточность в символы на своём выходе – для кодирования любого символа источника используются более длинные кодовые символы (3 двоичных символа вместо log2 M log2 6 2,585 двоичных символов).
121
Пример 2. Имеется источник без памяти с M 2 (таблица 2). Используем двоичный ( m 2 ) код Хаффмана для кодирования комбинаций символов источника длины k 1 .
Таблица 2. Таблица кодирования двоичным кодом Хаффмана при k 1 .
|
i |
ai A |
P(ai ) |
|
Кодовое дерево |
ci |
ni |
|
|||
|
0 |
a0 |
0,85 |
0 |
|
|
0 |
1 |
|
||
|
1 |
|
|
||||||||
|
1 |
a1 |
0,15 |
1 |
|
|
1 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Энтропия этого источника равна H (A) 0, 61 бит/(символ источника), а избыточность |
|||||||||||
|
|
A 1 |
H (A) |
|
1 |
0, 61 |
0,39 39% . |
|
|
||
|
|
log2 M |
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|||
Для этого кода средняя длина кодовой комбинации n 1 кодовый символ, избыточность С A 39% и коэффициент сжатия Rc 1, т.е. сжатия не происходит, а полученный код является примитивным двоичным кодом.
Эффективность кодирования данного кода равна |
1 |
C |
0 . |
|
|||
C |
|
A |
|
|
|
|
Согласно теореме Шеннона, чтобы повысить эффективность кодирования, необходимо увеличивать k . Выберем k 2 ( M 2k 4 ) и снова используем двоичный код Хаффмана.
Поскольку источник без памяти, то вероятность появления на его выходе различных последовательностей длины 2 можно рассчитать по формуле P(a1, a2 ) P(a1 )P(a2 ) . Исходные данные и результат кодирования представлены в таблице 3.
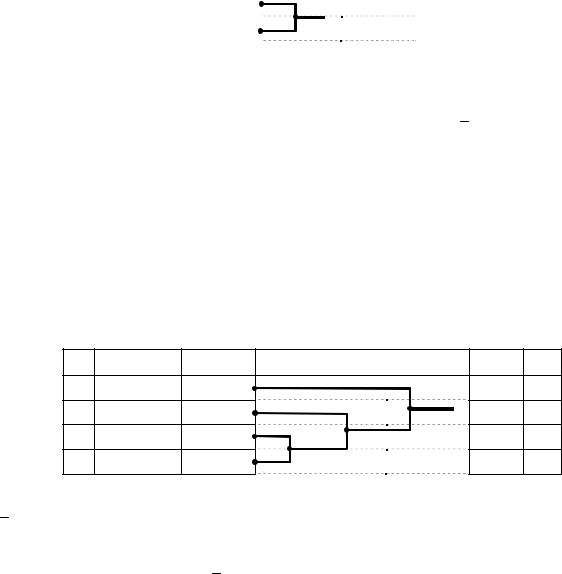
Таблица 3. Таблица кодирования двоичным кодом Хаффмана при k 2 . |
|
||||||
i |
a (ai , a j ) |
P(ai , a j ) |
Кодовое дерево |
ci |
ni |
||
0 |
( a0 , a0 ) |
0,7225 |
|
|
0 |
0 |
1 |
|
|
1 |
|||||
1 |
( a0 , a1 ) |
0,1275 |
|
0 |
10 |
2 |
|
|
|
||||||
0 |
0,2775 |
1 |
|||||
2 |
( a1 , a0 ) |
0,1275 |
1 |
|
110 |
3 |
|
0,15 |
|
||||||
3 |
( a1, a1 ) |
0,0225 |
1 |
|
|
111 |
3 |
|
|
|
|||||
Для этого кода средняя длина кодовой комбинации равна |
|
|
|||||
M 1
n P(ai )ni 1 0, 7225 2 0,1275 3 0,1275 3 0, 0225 1, 4275 [кодовых символов]
i 0 |
|
|
|
k log2 M |
|
2 |
|
|
|
|
|
|
||||||||
и |
|
|
R |
|
|
1, 4 раза. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
n |
|
log2 m |
|
1, 4275 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Избыточность вновь полученного кода равна |
|
|
|
|
||||||||||||||||
C |
1 |
H (C) |
1 |
|
k |
H (A) |
1 |
|
|
2 |
|
0, 61 |
0,145 14,5% . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
log2 m |
n log2 m |
1, 4275 |
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Эффективность кодирования данного кода достигает |
|
|||||||||||||||||||
|
|
|
1 |
C |
1 |
0,145 |
0,628 62,8% . |
|
||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
C |
|
|
A |
0,39 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно, увеличив длину информационных комбинаций от k 1 до |
k 2 , |
|||||||||||||||||||
удалось повысить эффективность кодирования на 62,8%. Большей эффективности кодирования можно добиться, если выбрать длину информационных комбинаций k 3 и более. Только в дальнейшем с увеличением k рост её будет значительно медленной.
122
Кроме кода Хаффмана существует множество других экономных кодов, например, экономный код Шеннона–Фано (1950). Считается, что он менее эффективный, но проще в реализации (не нужно строить кодовое дерево). При кодировании этим кодом все символы записываются в порядке убывания их вероятностей. Затем они делятся на m укрупнённых символов с приблизительно равными вероятностями. Каждому вновь полученному укрупнённому символу приписывается новый кодовый символ. Далее то же самое проделывается с каждым укрупнённым символом в отдельности.
Трудности практической реализации кодов Хаффмана и Шеннона–Фано
Для составления кодовых комбинаций необходимо знать априорную вероятность информационных комбинаций или укрупнённых символов источника P(ai ) . Априорные вероятности можно оценить, если перед кодированием сохранить в буфере памяти
переданное сообщение и |
рассчитать частость появления каждой информационной |
|||||
комбинации в сообщении. |
Частость – |
это оценка вероятности |
появления. |
Частость |
||
информационных комбинаций определяется по формуле |
ˆ |
/ Nобщ , где |
Ni – число |
|||
P(ai ) Ni |
||||||
появлений комбинации ai |
в сообщении, |
Nобщ |
– общее |
число комбинаций входящих в |
||
сообщение. Согласно теории вероятности P(ai ) |
lim Ni / Nобщ . |
|
|
|||
Следовательно, при кодировании необходимо: 1) задерживать целиком всё сообщение в буфере памяти; 2) рассчитывать оценки априорных вероятностей информационных комбинаций; 3) выполнить кодирование информационных комбинаций; 4) закодировать целиком всё сообщение; 5) к закодированному сообщению нужно добавить таблицу кодирования, по которой получатель смог бы правильно декодировать сообщение.
При практической реализации осуществить все этапы кодирования достаточно сложно. Поэтому используют субоптимальные способы кодирования, которые близки к оптимальным, но проще в реализации. Среди них можно выделить способы кодирования, в которых 1) используется заранее заданное распределение вероятностей информационных комбинаций, по которому формируются кодовые комбинации префиксного кода; 2) кодовые комбинации префиксного кода формируются по мере поступления данных в кодер.
В первом случае полученный код хорошо подходит для сжатия одних сообщений или данных, но плохо подходит для других. Во втором случае не учитывается распределение вероятностей символов. Второй способ кодирования используется для построения кодов, объединённых под общим названием ZIP коды. Основной вариант ZIP кода – код Лемпела– Зива (Lempel-Ziv) и различные его модификации используются в коммерческих программах сжатия (ZIP, GZIP, PKARC и др.).
Недостаток экономного кодирования
Основным недостатком экономного кодирования является его слабая защищённость от ошибок. Из-за устранения избыточности даже одиночная ошибка искажает сообщение так, что его невозможно полностью восстановить.
123
ЛЕКЦИЯ 16
Помехоустойчивое кодирование в каналах с шумом. Общие принципы обнаружения и исправления ошибок с помощью избыточных кодов по минимуму хэммингова расстояния. Оценки исправляющей и обнаруживающей способности блочного кода (кратности ошибок) по его минимальному хэммингову расстоянию. Оценки вероятностей ошибочного декодирования. Основные виды помехоустойчивых кодов. Системы декодирования с обратной связью.
Теорема Шеннона для непрерывного канала с шумом утверждает, что если производительность источника информации меньше пропускной способности канала H (A) C , то существуют способы кодирования и декодирования, при которых pb можно
сделать сколь угодно малой. Выбор одного из таких способов кодирования позволил бы передавать информацию по каналу фактически без ошибок.
Таким способом кодирования является помехоустойчивое кодирование. При помехоустойчивом кодировании в передаваемые данные вводят дополнительные или избыточные символы, которые называются проверочными символами. Проверочные символы используются для обнаружения и исправления ошибок в кодовых комбинациях.
При помехоустойчивом кодировании обычно m M и
R |
k |
1. |
(15) |
c n
Блочные коды
Кодовые комбинации блочного кода имеют постоянную и конечную длину n . Каждой кодовой комбинации соответствует определённая информационная комбинация длины k . Блочный код обозначается (n, k) .
Для построения кода |
необходимо |
из всех mn комбинаций выбрать mk кодовых |
|||
комбинаций. Такое отображение выполняет кодер. |
|
||||
Пример: n 4 , |
k 2 , m 2 : |
|
|
||
0 0 0 0 |
0 0 0 1 |
0 0 1 0 |
0 0 1 1 |
|
|
0 1 0 0 |
0 1 0 1 |
0 1 1 0 |
0 1 1 1 |
– всевозможные комбинации |
|
1 0 0 0 |
1 0 0 1 |
1 0 1 0 |
1 0 1 1 |
длины 4 |
|
1 1 0 0 |
1 1 0 1 |
1 1 1 0 |
1 1 1 1 |
|
|
|
|
|
|
|
– кодовые комбинации |
0 0 0 0 |
0 1 0 1 |
1 0 1 0 |
1 1 1 1 |
||
Конечное поле символов
В кодировании символы комбинаций рассматриваются как элементы некоторого поля. Поле – это набор элементов с однозначно заданными операциями сложения и умножения. Операции вычитания и деления являются обратными к сложению и умножению.
Поле с конечным числом элементов q называют полем Галуа и обозначают GF (q) . Свойства конечного поля:
1. Конечное поле может иметь число элементов равное q pv ,
где p – простое число, v 0 – целое число.
2. В любом поле существует только один нулевой элемент 0 и один единичный элемент
1, такие что 0 a a , 0 a 0 и 1 a a .
При v 1 поле является простым, потому что число его элементов равно простому числу q p . В простом поле операции сложения и умножения выполняются по модулю p .
При v 1 поле является расширением простого поля. Операции сложения и умножения элементов расширенного поля не выполняются по модулю q .
124
Например, при p 2 , GF (2) {0,1} и
Сложение |
Умножение |
+ |
|
0 |
1 |
· |
|
0 |
1 |
||
0 + 0 = 0 |
0 · 0 = 0 |
|
|
||||||||
0 + 1 = 1 |
0 · 1 = 0 |
|
0 |
|
0 |
1 |
|
0 |
|
0 |
0 |
1 + 0 = 1 |
1 · 0 = 0 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
||
1 + 1 = 1 |
1 · 1 = 1 |
|
|
|
|
|
|
|
|
|
|
Если q 22 |
4 , то GF (4) |
{0,1, 2,3} |
|
|
|
|
|
|
||||
|
+ |
0 |
1 |
2 |
3 |
· |
0 |
1 |
2 |
3 |
||
|
|
0 |
0 |
1 |
2 |
3 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
||
|
2 |
2 |
3 |
0 |
1 |
2 |
0 |
2 |
3 |
1 |
||
|
3 |
3 |
2 |
1 |
0 |
3 |
0 |
3 |
1 |
2 |
||
Векторное пространство Векторное пространство – это совокупность векторов, для которых заданы операции
сложения и умножения на скаляр. Если элементами векторов являются элементы некоторого поля, то векторное пространство линейное. Линейное векторное пространство Yn с векторами длины n должно удовлетворять условиям:
1.Существует единственный нулевой вектор 0 Yn , такой что 0 y y Yn .
2.Сумма любых векторов векторного пространства даёт вектор, который также принадлежит векторному пространству: yi y j yr Yn .
Векторное пространство, которое не удовлетворяет этим условиям, является
нелинейным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В дальнейшем для определённости будем рассматривать векторы-столбцы. |
|
||||||||||||||
Всевозможные комбинации длины n |
с элементами из простого поля GF ( p) |
( m p ) |
|||||||||||||
образуют линейное векторное |
пространство |
|
Yn , в котором операции сложения и |
||||||||||||
вычитания векторов выполняются поэлементно по модулю p : |
|
||||||||||||||
y1 y2 |
|
y3 , где y3,i |
y1,i |
y2,i mod p , |
|
||||||||||
a y1 |
|
y2 , где y2,i |
a y1,i mod p , |
|
|||||||||||
где i 0,1,..., n 1, a GF ( p) |
– скаляр. |
|
|
|
|
|
|
|
|
||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) при n 4 , m p 2 , |
y1 |
|
(1, 0, 0,1)T , |
y2 (1, 0,1,1)T |
|
||||||||||
y1 y2 (1, 0, 0,1)T (1, 0,1,1)T |
(0, 0,1, 0)T ; |
|
|||||||||||||
2) при m p 3 , y1 (1, 2, 2,1)T , |
|
y2 (2,1, 0,1)T |
|
|
|||||||||||
y1 y2 |
(1, 2, 2,1)T (2,1, 0,1)T |
(2,1, 2, 0)T . |
|
||||||||||||
Линейная комбинация векторов |
|
|
|
|
|
|
|
|
|||||||
В векторном пространстве сумма вида |
|
|
|
|
|
|
|
|
|||||||
a y |
0 |
a y |
1 |
... a |
r 1 |
y |
r 1 |
y Yn |
(16) |
||||||
|
0 |
|
1 |
|
|
|
|
|
|
||||||
называется линейной комбинацией векторов y0 ,..., yr 1 . |
|
||||||||||||||
Векторы y0 ,..., yr 1 называют линейно зависимыми, если существуют скаляры ai , |
|||||||||||||||
одновременно не равные нулю, при которых |
|
|
|
|
|
|
|
||||||||
|
a0y0 a1y1 ... ar 1yr 1 0 . |
(17) |
|||||||||||||
Для линейно независимых векторов y0 ,..., yr 1 |
|
||||||||||||||
|
a0y0 a1y1 ... ar 1yr 1 0 |
(18) |
|||||||||||||
при любых ai одновременно не равных нулю. |
|
|
|
|
|
|
|||||||||
125
Пространство кодовых комбинаций
Совокупность векторов векторного пространства образует подпространство. В подпространство можно включить векторы, которые совпадают с кодовыми комбинациями.
Тогда такое подпространство является пространством кодовых комбинаций Cn ( Cn Yn ).
Линейные коды
Для линейного кода пространство кодовых комбинаций Cn должно быть линейным (что возможно, если векторное пространство также линейное).
Свойства линейного кода:
1.Существует единственная нулевая кодовая комбинация 0 Cn , такая что 0 c c .
2.Сумма двух любых кодовых комбинаций снова даёт кодовую комбинацию:
ci c j cr Cn (свойство замкнутости). |
(19) |
Для построения линейного (n, k) кода достаточно в линейном векторном пространстве |
|
Yn выбрать k линейно независимых векторов g0 ,..., gk 1 Yn . Тогда |
любую кодовую |
комбинацию линейного кода можно найти как линейную комбинацию этих векторов: |
|
c b0g0 b1g1 ... bk 1gk 1 , |
(20) |
где bi – некоторые коэффициенты.
Можно убедиться, что оба свойства линейного кода удовлетворяются. Следовательно,
всевозможные комбинации символов b определяют все комбинации c линейного кода Cn . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
Символы bi называются информационными символами. |
|
||||||||||||
В матричной форме записи |
c G b , |
|
|
(21) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
где b (b , b ,..., b |
)T |
– вектор-столбец информационных символов или информационная |
|||||||||||
0 1 |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
комбинация, G g0 |
|
|
g1 |
|
... |
|
gk 1 |
– порождающая матрица кода размера n k . |
|||||
|
|
|
|||||||||||
|
|
|
|||||||||||
|
|
|
|
||||||||||
Использование порождающей матрицы упрощает построение и кодирование блочных |
|||||||||||||
линейных кодов. |
|
|
|
|
m p 2 . Для построения |
|
|
|
|||||
Пример: n 5 , |
|
кода (5,2) выберем k 2 произвольных |
|||||||||||
линейно независимых |
|
вектора. |
Например: g |
0 |
(1, 0,1,1,1)T и |
g (0,1,1, 0,1)T . Можно |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
убедиться, что они линейно независимые, т.е. ни при каких b0 и b1 , принадлежащих полю GF (2) и одновременно не равных нулю,
b0g0 b1g1 0 .
Тогда все Nк.к 2k 4 кодовые комбинации можно найти по формуле (21), в которой
b (b |
,b )T |
– вектор-столбец из k 2 информационных символов, |
|
||||
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
G g0 |
|
g1 |
1 |
1 |
(22) |
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
– порождающая матрица кода размера 5 2 .
Таблица кодирования для двоичного кода (5,2).
№ |
bT (b0 , b1 ) |
cT (c0 , c1, c2, c3 , c4 ) |
0 |
0 0 |
0 0 0 0 0 |
1 |
0 1 |
0 1 1 0 1 |
2 |
1 0 |
1 0 1 1 1 |
3 |
1 1 |
1 1 0 1 0 |
126

Систематический и несистематический коды
Если при кодировании информационные комбинации входят в кодовую комбинацию в явном виде, то такой код называют систематическим кодом: c (c0 , c1, c2 ,..., cn 1 ) (b0 ,..., bk 1, k ,..., n 1 ) . Иначе код является несистематическим.
Для систематического кода порождающая матрица имеет следующую структуру
G |
Ik |
, |
(23) |
||
|
Γ |
|
|||
|
|
|
|
|
|
где Ik – единичная матрица размера k k , Γ – матрица проверочных символов кода, размера
(n k) k .
|
Построенный ранее код (5,2) является систематическим по первым двум кодовым |
|||||||||
|
|
|
1 |
0 |
1 |
1 |
|
|
||
символам: |
I2 |
Γ 1 |
0 . |
|
|
|||||
0 |
1 , |
|
|
|||||||
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Любой несистематический линейный блочный код можно привести к |
|||||||||
систематическому коду путём перестановок строк и столбцов |
порождающей матрицы: |
|||||||||
G |
P G |
|
P |
Ik |
|
, где |
P , |
P – перестановочные матрицы |
(единичные матрицы с |
|
|
|
|||||||||
сист |
1 |
несист |
2 |
Γ |
|
1 |
2 |
|
||
|
|
|
|
|
||||||
переставленными столбцами и строками).
Проверочная матрица кода
Проверочная матрица кода H – это матрица размера порождающей матрице G :
HTG 0 .
Проверочная матрица систематического кода равна:
ΓT H I .
n k
n (n k) , которая ортогональна
(24)
(25)
Из определения следует также, что если c – кодовая комбинация, то
|
|
|
|
HTc 0 . |
|
|
|
|
(26) |
||||||
Проверочная матрица используется для обнаружения и дальнейшего исправления |
|||||||||||||||
ошибок в кодовых комбинациях. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверочная матрица рассмотренного кода (5,2) равна |
|||||||||||||||
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
||||
|
ΓT |
1 |
|
|
0 |
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
H |
1 |
|
|
0 |
|
|
0 . |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
I3 |
1 |
|
|
||||||||||
|
|
|
|
|
|
|
0 |
|
|
0 |
|||||
|
|
|
|
|
|
|
0 |
0 |
|
|
1 |
||||
Дуальный код
Если в качестве порождающей матрицы использовать проверочную матрицу H , а вместо проверочной матрицы порождающую матрицу G , то полученный таким образом код называют дуальным кодом.
Дистанционные свойства в пространстве комбинаций
Вес комбинации (y) – число ненулевых символов в комбинации y . Например,
y (1, 0,1,1, 0)T , вес (y) 3 ; y (1, 0, 2,1, 2)T , вес (y) 4 . |
|
|
|
Расстояние по Хэммингу d (yi , y j ) |
между комбинациями yi |
и y j |
– это число позиций, |
в которых символы комбинаций yi и y j |
не совпадают. |
|
|
В линейном пространстве d (yi , y j ) |
равно весу комбинации yi |
y j |
: |
127
|
|
d (yi , y j ) (yi y j ) . |
|
|
|
|
(27) |
Например, при p 3 для комбинаций y1 (1, 2, 2,1)T |
и y2 (2,1, 0,1)T , а d (y1, y2 ) 3 . |
||||||
Свойства d (yi , y j ) : |
|
|
|
|
|
||
1) |
|
d (yi , y j ) 0 . |
|
|
|
|
(28) |
2) |
|
d (yi , y j ) d (y j , yi ) . |
|
|
|
|
(29) |
3) |
d (yi , y j ) d (yi , yr ) d (y j , yr ) (неравенство треугольника). |
|
|
||||
Для кодовых комбинаций линейного кода из свойства замкнутости следует: |
|||||||
4) |
|
d (ci , c j ) (ci c j ) (cr ) , |
|
|
|
|
(30) |
где cr |
ci c j Cn . |
|
|
|
|
|
|
Минимальное расстояния кода – это минимальное расстояние по Хэммингу между |
|||||||
всеми парами различных кодовых комбинаций: |
|
|
|
|
|
||
|
|
dmin min d (ci , c j ) . |
|
|
|
|
(31) |
|
|
i, j |
|
|
|
|
|
|
|
i j |
|
|
|
|
|
Например, |
кодовые комбинации кода (5,2) равны |
c |
0 |
(0, 0, 0, 0, 0)T , |
c |
(0,1,1, 0,1)T , |
|
|
|
|
|
|
1 |
||
c3 (1, 0,1,1,1)T , |
c4 (1,1, 0,1, 0)T . Путём попарного вычисления расстояния |
по Хэммингу |
|||||
между всеми кодовыми комбинациями находим, что минимальное расстояние кода равно
dmin 3 .
Для линейных кодов минимальное расстояние кода находится значительно проще, а именно, оно равно наименьшему весу ненулевой кодовой комбинации (следует из 4 свойства):
|
dmin |
min (ci ) . |
(32) |
||
|
|
ci 0 |
|
|
|
Например, распределение весов рассмотренного кода (5,2) следующее |
|||||
|
Таблица весов кодовых комбинаций кода (5,2). |
||||
|
ciT |
|
|
(ci ) |
|
|
0 0 0 0 0 |
|
|
0 |
|
|
0 1 1 0 1 |
|
|
3 |
|
|
1 0 1 1 1 |
|
|
4 |
|
|
1 1 0 1 0 |
|
|
3 |
|
Минимальный вес, не равный нулю, равен 3. Следовательно, минимальное расстояние
кода равно dmin 3 . |
|
|
|
|
{ni } 1, n1 , n2 |
,..., nn , каждое из |
|
|
Спектр кода – это совокупность чисел |
которых |
|||||||
определяет число кодовых комбинаций с весом равным i , где i 0,1,..., n . |
|
|
||||||
Например, спектр кода (5,2) следующий: n0 |
1, n1 0 , n2 |
0 , n3 2 , n4 |
1, n5 |
0 или |
||||
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
ni 1, 0, 0, 2,1, 0 .
Спектр кода позволяет рассчитать вероятность необнаруженной ошибки и другие характеристики кода.
Передача кодовых комбинаций по дискретному симметричному каналу без памяти
В линейном пространстве комбинацию на выходе дискретного канала с аддитивным шумом можно определить выражением
y ci e , |
(33) |
где ci – переданная i-я кодовая комбинация длины |
n , e – комбинация случайных |
ошибочных символов длины n . |
|
128
В дискретном симметричном канале без памяти вероятность перехода кодовой комбинации ci в комбинацию y (функция правдоподобия) равна
|
p |
|
d (y,ci ) |
d (y,c |
|
|
|
||
|
n |
) |
|
|
|||||
P(y | ci |
) |
|
|
|
(1 p) |
i |
|
, |
(34) |
|
|
||||||||
|
m 1 |
|
|
|
|
|
|
||
где p – вероятность ошибки символа, m – позиционность символов. |
|
||||||||
Из этой формулы следует, |
что наиболее вероятными ошибками в канале являются |
||||||||
одиночные ( d (y, ci ) 1 ), далее двойные ( d (y, ci ) 2 ), тройные и т.д.
Правило максимума правдоподобия при декодировании кодовых комбинаций (режим исправления ошибок):
iˆ arg max P(y | ci ) . |
(35) |
i 0,1,...,mk 1 |
|
Для дискретного симметричного канала без памяти правило максимума правдоподобия совпадает с правилом минимума расстояния:
iˆ arg max P(y | ci )
i 0,1,...,mk 1
или
|
|
p |
|
d (y,ci ) |
n d (y,ci ) |
||
arg max |
(1 p) |
||||||
|
|
|
|
|
|||
i 0,1,...,mk 1 |
m 1 |
|
|
|
|||
iˆ arg min d (y, ci ) .
i 0...mk 1
arg maxk |
|
p |
|
d (y,ci ) |
|
|
|
|
|
(1 p)(m 1) |
|
|||
i 0,1,...,m 1 |
|
|
|
(36)
Алгоритм или правило минимума расстояния состоит в выборе в качестве решения той кодовой комбинации, которая ближе всех по Хэммингу к принятой комбинации.
Переданная |
ci |
y1 |
|
y2 |
y3 |
y4 |
c j |
Ближайшая к |
||
кодовая |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
переданной |
|
|
|
|
|||||||
комбинация |
|
|
|
|
кодовая |
|||||
|
|
|
|
|
dmin |
5 |
|
|
|
комбинация |
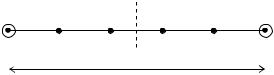
Рис. 3. Ближайшие друг к другу кодовые комбинации |
||||||||||
Например, если при |
передаче |
|
кодовой |
комбинации |
ci |
будет принята любая из |
||||
следующих комбинаций ci |
, |
|
y1 или y2 , то декодер по минимуму расстояния сделает решение |
|||||||
в пользу ci . Если же будет принята любая комбинация с другой половины, то декодер вынесет решение в пользу c j .
Декодирование блочных кодов Табличное декодирование блочных кодов. При реализации декодеров по минимуму
расстояния для кодов с небольшим числом кодовых комбинаций, исправляющих не менее t ошибок, составляют таблицу декодирования, в которой всевозможные ошибочные (запрещённые) комбинации объединяются с ближайшими по Хэммингу кодовыми комбинациями.
Таблица декодирования комбинаций линейного кода (стандартное расположение).
кодовые комбинации |
c0 0 |
c1 |
… |
|
cmk 1 |
Разрешённые |
|||
|
комбинации |
||||||||
обнаруживаемые и |
e1 |
c1 e1 |
… |
cmk 1 e1 |
|
||||
e2 |
c1 e2 |
… |
cmk 1 e2 |
|
|||||
исправляемые |
|
||||||||
ошибочные комбинации |
… |
… |
… |
|
|
… |
|
||
(ei ) t |
er |
c1 er |
… |
c |
k |
1 |
er |
Запрещённые |
|
|
|
|
|
|
m |
|
комбинации |
||
обнаруживаемые |
er 1 |
c1 er 1 |
… |
cmk |
1 er 1 |
||||
|
|||||||||
или исправляемые при |
|
|
|
|
|
|
|
||
… |
… |
… |
|
|
… |
|
|||
полном декодировании |
|
|
|
||||||
|
|
|
cmk 1 eR |
|
|||||
(ei ) t |
eR |
c1 eR |
… |
|
|||||
129
