
Конспект лекции по ТЭС
.pdf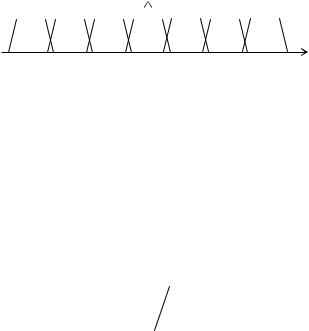
Погрешности дискретизации и восстановления сигнала
1. Неверный выбор fд . Если сигнал имеет более широкий спектр, чем значение fд / 2 ,
то при дискретизации произойдёт наложение спектров. Это приведёт к искажению спектра исходного сигнала и, следовательно, полностью восстановить сигнал по его отсчётам становится невозможным.
|
|
|
|
|
|
|
|
Sxд |
( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 fд |
fд |
0 |
|
|
fд |
|
2 fд |
|
f |
|||||
Рис. 13. Наложение спектров дискретизированного сигнала при fд 2Fс . |
|||||||||||||||||
Для устранения этого недостатка можно: 1) увеличивать |
fд до требуемого значения по |
||||||||||||||||
теореме Котельникова; 2) перед дискретизацией пропустить такой сигнал через ФНЧ с частотой среза fср fд / 2 . Использование ФНЧ позволяет устранить наложение спектров, но
это также приводит к искажению входного сигнала x(t) .
Если обозначить x (t) – |
|
|
|
|
сигнал на |
выходе такого фильтра, то абсолютную и |
||||||
относительную ошибку восстановления сигнала можно найти по формулам |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ex |
|
|
|
x(t) x (t) |
|
|
|
2 (x(t) x (t))2 dt 2 | Sx ( f ) |2 df , |
(68) |
|||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Fв |
|
|
|
|
|
|
Ex |
|
|
|
|
|
|
|
|
|
|
|
|
| Sx ( f ) |2 |
df | Sx ( f ) |2 df . |
(69) |
|||||
|
|
|
|
Ex |
||||||||
|
|
|
|
|
|
|
|
|
F |
0 |
|
|
2. Неидеальность |
ФНЧ. |
|
|
|
|
с |
|
|
||||
|
|
Идеальный |
ФНЧ физически реализовать |
невозможно, |
||||||||
поскольку его ИХ имеет бесконечную длительность. Физически реализуемые ФНЧ, например фильтры Баттерворта и Чебышева, имеют неравномерную АЧХ в полосе пропускания и некоторую полосу расфильтровки. Если полосу расфильтровки можно учесть выбором fд , то неравномерность АЧХ практически устранить невозможно.
3. Ограничение сигнала во времени. Если fд выбрана правильно и для
восстановления выбран идеальный ФНЧ, то восстановленный после дискретизации сигнал будет иметь бесконечную длительность.
Если сигнал рассматривать на интервале времени длительностью Tс , то число отсчётов,
входящих в рассматриваемый интервал, равно N T |
/ t |
f |
T . Тогда восстановленный |
c |
|
д |
c |
сигнал на этом интервале можно представить приближённо в виде усечённого ряда
Котельникова
|
|
|
|
N 1 |
sin fд (t k t) |
|
|
|||||
x(t) xN (t) xk |
|
. |
(70) |
|||||||||
fд (t k t) |
||||||||||||
|
|
|
|
k 0 |
|
|
||||||
Погрешность восстановления сигнала в этом случае можно рассчитать по формуле |
|
|||||||||||
|
|
|
|
|
|
|
|
|
Tс |
|
|
|
Ex |
|
|
|
x(t) xN (t) |
|
|
|
2 x(t) xN (t) 2 dt , |
(71) |
|||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Число отсчётов, достаточных для восстановления сигнала с помощью ряда |
||||||||||||
Котельникова, численно равно базе сигнала. |
|
|
|
|||||||||
База сигнала – это произведение B 2FcTc , где Fc – ширина спектра сигнала, |
Tc – |
|||||||||||
длительность сигнала. Сигналы с базой порядка единицы являются простыми сигналами. Сложные сигналы имеют базу во много раз большую единицы ( B 1). Примером простого сигнала является одиночный прямоугольный импульс, отрезок гармонического колебания и другие сигнальные импульсы. К сложным сигналам относят составные сигналы, состоящие из простых сигналов, широкополосные сигналы и др.
20
Другие способы дискретизации. Дискретизация “выборка-хранение”
На практике наиболее популярным способом дискретизации является дискретизация “выборка-хранение”. При этом способе дискретизации дискретизированный сигнал получается в результате свёртки одиночного прямоугольного импульса единичной высоты f t (t) и длительности t с сигналом, полученным в результате идеальной дискретизации:
|
|
|
|
xд (t) f t (t) *[x(t)xр (t)] |
xk f t (t k t) , |
(72) |
|
|
k |
0 t t; |
|
где знак “* ” обозначент свёртку сигналов, а f t |
1, |
|
|
(t) |
иначе. |
|
|
|
0, |
|
|
Свёртка сигналов во временной области соответствует произведению |
их спектров. |
||
Поэтому спектральная плотность сигнала, полученного при дискретизации “выборкахранение”, равна
|
|
Sxд ( f ) S f t |
|
|
|
|
|
|
|
|
|
||||
|
|
( f ) fд |
|
|
Sx ( f k fд ) , |
(73) |
|||||||||
где |
|
|
|
|
k |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
t |
|
|
|
|
|
sin(f t) |
|
|
||
S f t ( f ) |
f t (t) e j 2 f t |
dt e j 2 f t dt |
e j f t . |
(74) |
|||||||||||
|
|
||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
f |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если выполняются условия теоремы Котельникова, то |
|
||||||||||||||
|
|
|
|
sin(f t) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
Sxд ( f ) |
|
|
|
|
Sx ( f |
k fд ) |
. |
(75) |
||||||
|
f t |
||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||
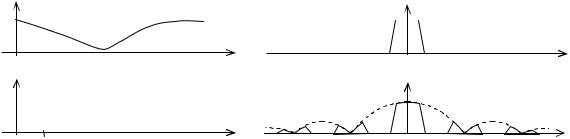
Следовательно, с увеличением частоты спектр дискретизированного сигнала убывает по закону sin(x) / x . Убывание спектра позволяет ослабить требования к реализации фильтравосстановителя, т.к. в этом случае проще подавить частотные составляющие сигнала за пределами fср .
Недостатком этого способа дискретизации является неравномерное ослабление спектра исходного сигнала, что приводит к возникновению искажений при его восстановлении. Для компенсации искажений используют фильтр-восстановитель с АЧХ, обратной амплитудно-частотному спектру импульса f t (t) .
x(t) |
|
|
|
|
|
|
|
Fс |
|
|
|
Sx ( f ) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xд (t) |
t |
|
|
|
|
|
|
0 Fс |
|
|
|
|
|
|
f |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sxд ( f ) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
t |
2 |
|
fд |
f |
|
д |
Fс |
0 Fс |
fд |
2 fд |
f |
||||||||||||||||||
Рис. 14.
21
Квантование отсчётов по уровню и кодирование. Цифровой сигнал
После дискретизации каждый отсчёт xk x(k t) квантуют по уровню. Для этого выбирается конечное множество уровней xk(i ) , где i 0,1,.., L 1 , L – общее число уровней
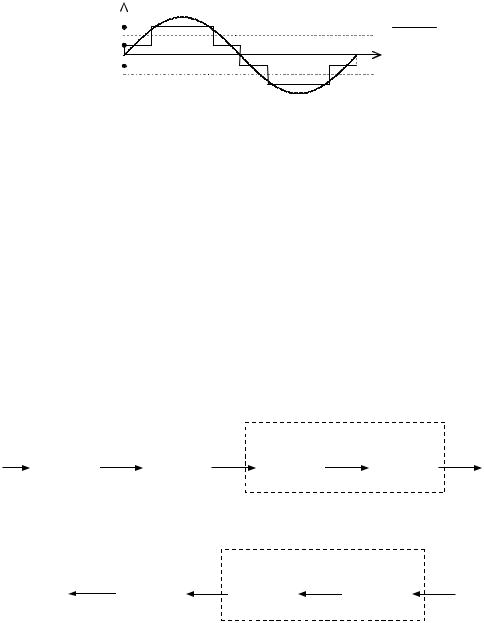
квантования, обычно L 2n , и каждый отсчёт дискретизированного сигнала заменяется ближайшим к нему уровнем. Разница между отсчётом и выбранным уровнем квантования определяет ошибку квантования k xk xk(i ) , а сигнал разности (t) xд (t) xкв (t) является
шумом квантования. На следующем рисунке показаны примеры квантования сигнала на 4 уровня.
x(t)
xmax |
x xmax xmin |
11 |
|
|
L |
10
t
01
00 
 x
x
xmin
Рис. 15. Примеры квантования сигнала на L = 4 уровня.
Если мгновенные значения сигнала случайные, равномерно распределённые на интервале (xmax ; xmin ) , то мощность шума квантования можно рассчитать по формуле
( x)2 /12 .
Каждому уровню квантования сопоставляют определённое число, обычно равное номеру уровня квантования i , и каждый отсчёт заменяется соответствующим ему номером
уровня квантования. |
Номер уровня квантования кодируется в последовательность из |
log2 L n двоичных |
символов bk (bk ,0 , bk ,1 ,..., bk ,n 1 ) (номер уровня в двоичной системе |
счисления). Эти двоичные символы и выдаются на выходе АЦП. Двоичные символы bk образуют цифровой сигнал b(t) , представляющий собой последовательность биполярных прямоугольных импульсов длительности T t / n .
Структурные схемы АЦП и ЦАП
x(t) |
|
x (t) |
|
|
|
xд (t) |
Импульсно-кодовый модулятор (ИКМ) |
b(t) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ФНЧ |
|
|
Дискретиза- |
|
xk |
|
Квантователь |
|
xk(i) |
|
Кодер уровней |
|
bk |
|||||
|
|
|
тор |
|
|
|
по уровню |
|
|
|
|
квантования |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Рис. 16. Структурная схема АЦП. |
|
|
|
||||||||||||
|
|
|
|
|
xд (t) |
|
Импульсно-кодовый демодулятор |
b(t) |
|
||||||||||
|
x(t) |
|
|
|
|
|
|
xk(i) |
|
|
|
|
|
|
|||||
|
|
|
ФНЧ |
|
|
|
Формиро- |
|
|
Декодер |
|
bk |
|
||||||
|
|
|
(фильтр-восстано- |
|
|
|
ватель |
|
|
|
|
уровней |
|
|
|
|
|||
|
|
|
витель) |
|
|
|
импульсов |
|
|
|
квантования |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 17. Структурная схема ЦАП.
22

ЛЕКЦИЯ 6
ОСНОВЫ ТЕОРИИ МОДУЛЯЦИИ И ДЕТЕКТИРОВАНИЯ
Модуляция. Особенности преобразований сигналов и их спектров в нелинейных и параметрических цепях. Аппроксимация ВАХ. Методы расчета спектров сигналов на выходе нелинейной цепи (методы кратных углов, угла отсечки, трех ординат). Умножение частоты. Преобразование частоты квазигармонических сигналов в нелинейных и параметрических цепях, его применения в технике связи.
Для согласования источника сообщений с каналом используют модуляцию. Модуляция – изменение одного или нескольких параметров несущего сигнала
(переносчика, несущей) по закону модулирующего (первичного) сигнала.
В качестве несущего сигнала выбирается такой сигнал, который с наименьшими затратами смог бы донести сообщение до получателя.
Чаще всего в качестве несущего сигнала используют гармоническое колебание uнес (t) U cos(t ) . У такой несущей можно изменять 3 свободных параметра: U , , .
Устройство, выполняющее модуляцию, называется модулятором. На приёмной стороне производится операция обратная модуляции – демодуляция или детектирование. Устройство, выполняющее детектирование называется детектором.
Одной из основных задач модуляции является перенос спектра первичного сигнала на заданную высокую частоту. Эту операцию называют транспонированием спектра сигнала.
Линейные системы с постоянными параметрами не могут транспонировать спектр сигнала. Для линейной системы с постоянными параметрами справедлив принцип суперпозиции:
1) T[u1(t) u2 (t)] T[u1 (t)] T[u2 (t)] , 2) T[ u(t)] T[u(t)],
где T[ ] – оператор преобразования, – константа.
Поэтому, любой гармонический сигнал, прошедший через линейную систему, сохраняет и свою форму, и форму своего спектра. Для транспонирования спектра сигнала, умножения частоты и других подобных операций используют нелинейные системы, в
которых |
выходной |
сигнал связан с входным сигналом нелинейной |
зависимостью |
uвых (t) |
f uвх (t), t . |
Если нелинейная функция f (x,t) не зависит от времени, |
f (x,t) f (x) , |
то такую систему называют безинерционной нелинейной системой.
Нелинейные системы обладают большими возможностями для обогащения спектра сигнала. В качестве нелинейных элементов (НЭ) можно использовать полупроводниковые диоды, биполярные и полевые транзисторы. НЭ описываются вольтамперной характеристикой (ВАХ), для которой входным воздействием является напряжение, а выходным – ток.
Сопротивление постоянному току нелинейного элемента определяется по ВАХ при подаче на его вход постоянного напряжения U0 : R U0 / I0 . Если выбрать рабочую точку
(Uр , Iр ) на ВАХ и задать приращение напряжения u , то можно найти дифференциальное сопротивление нелинейного элемента
Rдиф du / di u Uр u / i .
Иногда удобнее пользоваться дифференциальной крутизной
Sдиф 1/ Rдиф di / du u Uр ,
которая является тангенсом угла наклона касательной в рабочей точке.
23
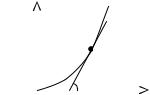
i , мА
Iр
0 Uр u , В
Рис. 18. Вольтамперная характеристика НЭ.
Аппроксимация ВАХ
Для удобства расчётов реальную ВАХ заменяют приближённой и более простой при математическом описании кривой. Такую замену называют аппроксимацией. Сществуют различные способы аппроксимации.
Полиномиальная (степенная) аппроксимация
Этот способ основан на разложении нелинейной ВАХ в ряд Тейлора в окрестности рабочей точки:
i a0 a1 (u Uр ) a2 (u Uр )2 ... an (u Uр )n .
Чем больше степень полинома, тем точнее будет расчёт тока, но резко возрастает сложность вычислений. Полином с малой степенью хорошо описывает небольшой участок ВАХ. Поэтому полиномиальную аппроксимацию обычно используют при слабых входных сигналах. При сильных сигналах, когда сигнал изменяется в большом диапазоне, резко возрастает погрешность аппроксимации и падает точность результатов.
Кусочно-линейная аппроксимация
При таком способе аппроксимации ВАХ приближённо заменяется ломаной линией, состоящей из двух отрезков прямой линии:
0, |
u Uотс , |
i |
u Uотс , |
S (u Uотс ), |
где Uотс – напряжение отсечки, S – крутизна линейного участка ВАХ.
Этот способ аппроксимации используется при сильном входном сигнале.
Показательная (экспоненциальная) аппроксимация
При показательной аппроксимации ВАХ НЭ описывается следующей зависимостью i I ea u 1 ,
где I и a – заданные константы.
Показательную аппроксимацию обычно используют для описания ВАХ диода.
24

Расчёт спектров тока на выходе нелинейного элемента
Метод кратных углов
Метод кратных углов используется при полиномиальной аппрокисмации ВАХ НЭ. Если на вход НЭ подаётся напряжение
u(t) Eсм Um cos(1t) ,
то для простоты расчётов удобно выбрать в качестве рабочей точки Uр Eсм . Следовательно, ВАХ будет аппроксимироваться полиномом
|
i a |
a (u E |
) a |
(u E |
)2 ... a |
(u E |
см |
)n . |
||||||
0 |
1 |
|
см |
2 |
|
см |
n |
|
|
|
||||
Подставив в этот полином вместо u |
входное напряжение u(t) и используя формулы |
|||||||||||||
кратных углов |
|
|
|
|
|
|
|
|
|
|
|
|
||
cos2 |
1 cos 2 |
, |
cos3 |
|
3cos cos 3 |
, cos4 |
3 4 cos 2 cos 4 |
, |
||||||
|
|
|
||||||||||||
2 |
|
|
|
|
4 |
|
|
|
|
|
|
8 |
|
|
cos5 10 cos 5cos 3 cos 5 и т.д., 16
непосредственно получим разложение тока в ряд Фурье
i(t) I0 I1 cos(1t 1 ) I2 cos(21t 2 ) I3 cos(31t 3 ) ... In cos(n 1t n )
или
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i(t) Ik |
cos(k 1t k ) , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
|
|
|
I |
|
|
|
a |
a U 2 |
|
a U 4 ... |
|
|
|
|
|
|
|
I |
|
|
|
|
a U |
|
a U 3 |
a U 5 |
|
|
||||||||||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
... |
, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
0 |
2 |
|
2 m |
8 |
4 m |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 m |
|
|
3 m |
8 5 m |
|
|
|||||||||||||||||||
|
I |
|
|
|
1 |
a U 2 |
|
1 |
a U 4 |
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
1 |
a U 3 |
|
5 |
a U |
5 ... |
|
|
||||||||||||||||
|
|
|
|
|
... |
, |
|
|
|
|
|
|
|
|
|
|
|
|
и т.д. |
|||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 m |
8 |
|
4 m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 3 m |
|
|
16 5 m |
|
|
|
||||||||||||||
Если амплитуда входного напряжения мала, то ВАХ достаточно аппроксимировать |
||||||||||||||||||||||||||||||||||||||||||||||||||
полиномом 2 степени относительно рабочей точки: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i a a (u E ) a |
|
(u E )2 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 |
|
см |
2 |
|
|
|
|
|
|
|
см |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i I0 |
I1 cos(1t 1 ) I2 cos(21t 2 ) , |
|
|
|
|
|
||||||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
a U 2 |
|
|
|
|
I |
|
|
|
a U |
|
|
I |
|
|
a U 2 |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
|
a |
, |
|
|
|
1 |
|
|
, |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
2 2 m |
|
|
|
|
|
|
|
|
1 m |
|
|
|
|
2 2 m |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Аналогично можно рассчитать ток на выходе НЭ при подаче на его вход суммы двух и более гармонических колебаний различных частот. При этом в спектре тока будут содержаться комбинационные частоты fк | n1 f1 n2 f2 n3 f3 ... | , где ni – любые целые
числа. Порядок комбинационной частоты находится по формуле N | n1 | | n2 | | n3 | ... .
Метод угла отсечки
Метод угла отсечки используется при кусочно-линейной аппроксимации ВАХ, когда линейный участок ВАХ нелинейного элемента заменяется прямой линией, а остальная часть заменяется горизонтальной прямой совпадающей с осью абсцисс.
ВАХ НЭ при кусочно-линейной аппроксимации
0, |
u Uотс , |
i |
u Uотс , |
S (u Uотс ), |
где Uотс – напряжение отсечки, S – крутизна линейного участка ВАХ.
25

i, мА |
|
|
|
|
|
i(t) |
|
|
|
|
|
|
|
imax |
|
0 |
|
|
|
u , В |
0 |
1t |
|
Eсм U |
отс |
Um |
u(t) |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1t
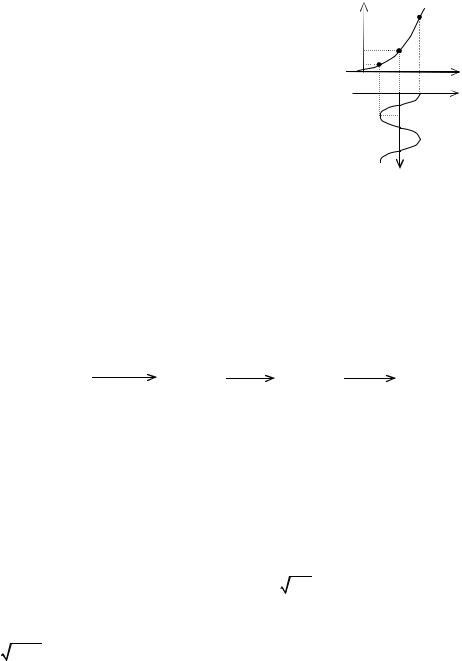
Рис. 19. Кусочно-линейная аппроксимация ВАХ НЭ.
При подаче на вход гармонического напряжения u Eсм Um cos(1t) , на выходе НЭ
будут действовать периодические импульсы тока, повторяющие входное гармоническое колебание в течение отрезка времени длительностью 2 . Из графика можно определить угол отсечки :
Uотс Eсм Um cos .
Откуда
cos Uотс Eсм , 0 .
Um
Разложив в ряд Фурье выходной пульсирующий ток ( i(t) –чётная, bk 0 ), получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i(t) a0 ak cos(1kt) , |
i(t) Ik cos(1kt k ) |
|
где |
|
|
|
|
|
|
|
k 1 |
k 0 |
|
|
|
|
|
|
|
ak SUm k ( ) , |
Ik SUm | k ( ) | |
|
|
|
|
|
|
|
|
|
||
0 () |
|
1 |
|
(sin cos ) – коэффициент Берга 2 рода для постоянной составляющей, |
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
1 () |
1 |
|
( sin cos ) – коэффициент Берга 2 рода для 1-й гармоники, |
||||||
|
|
||||||||
|
|
|
|
|
|
||||
|
k |
( ) |
|
2 sin(k) cos( ) k cos(k) sin( ) |
– коэффициенты Берга 2 рода при k 1 . |
||||
|
|
|
|
k(k 2 1) |
|||||
|
|
|
|
||||||
Максимальное |
значение тока равно |
imax S(Eсм Um Uотс ) SUm (1 cos( )) . Тогда |
|||||||
спектральные составляющие тока на выходе можно выразить через максимальное значение тока по формуле
|
|
|
Ik |
imax | k ( ) | , |
|
|||
где k ( ) |
k ( ) |
– коэффициенты Берга 1 рода. |
|
|||||
1 cos( ) |
|
|||||||
|
|
|
|
|
|
|
||
При 0 , |
ток на выходе НЭ |
равен нулю, а при – |
Eсм Uотс Um и сигнал |
|||||
полностью попадает на линейный участок ВАХ (линейный режим работы НЭ). |
||||||||
Если требуется максимизировать амплитуду n-й гармоники тока In на выходе НЭ |
||||||||
относительно , то оптимальным значением угла отсечки является |
|
|||||||
|
|
|
/ n, |
при Um const; |
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
опт |
, |
при imax const. |
|
||
|
|
|
|
3n |
|
|||
|
|
|
|
|
|
|
||
Условие imax const применяют для выходных каскадов передатчика.
26
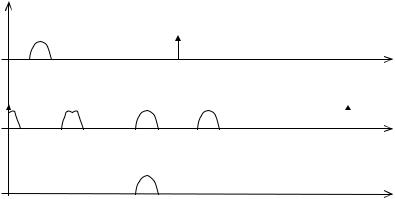
Метод трёх ординат
В методе трёх ординат приближённо рассчитывают амплитуды первых трёх гармоник
тока на выходе: I0 , I1, I2 . При этом полагают, что |
|
|
||||
|
|
i(t) a0 |
a1 cos(1t) a2 cos(21t) . |
|
||
На ВАХ при 1t |
0, / 2, |
определяют три ординаты a , b и c , которые задают |
||||
систему линейных уравнений |
|
i |
|
|||
A a0 a1 a2 , |
при 1t 0 ; |
A |
|
|||
C |
|
|||||
B a0 |
a2 , |
при 1t / 2 ; |
|
|||
|
|
|
|
B |
|
|
C a0 |
a1 a2 , |
при 1t . |
0 |
u |
||
u(t) |
||||||
Решение этой системы следующее: |
|
|
||||
|
|
/ 2 |
||||
I0 | A 2B C | / 4 , |
|
|
|
|||
I1 | A C | / 2 , |
|
|
|
1t |
||
I2 | A 2B C | / 4 . |
|
|
||||
Расчитанные амплитуды гармоник тока будут достаточно точными, если ВАХ хорошо аппроксимируется полиномом второй степени.
Умножение частоты
Умножение частоты это операция, при которой частота входного гармонического колебания увеличивается в целое число раз. Умножение частоты используется для получения колебаний кратных частот от задающего генератора (например, кварцевого генератора) в системах синхронизации, от вспомогательного генератора – гетеродина в модуляторах и демодуляторах, и др.
uвх (t) |
|
i(t) |
|
uвых (t) |
|
НЭ |
ПФ |
||||
|
|
|
|||
|
|
|
|
|
Рис. 20. Структурная схема умножителя частоты.
Если подать на НЭ гармоническое колебание некоторой частоты uвх (t) Um cos 1t , то на выходе получим ток
i(t) Ik cos(k 1t k ) .
k 0
Полосовой фильтр (ПФ) выделяет гармоническое колебание нужной кратности. Если в качестве ПФ используют резонансный LC-контур, то его резонансная частота равна
|
|
fрез |
n f1 |
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
||||||
|
|
|
|
LC |
|
|
|||
На резонансной частоте сопротивление LC-контура будет максимальным: |
|||||||||
|
|
|
Rрез Q , |
|
|
|
|
|
|
где |
|
– характеристическое |
сопротивление |
контура, |
Q – добротность |
||||
L / C |
|||||||||
колебательного контура.
Поскольку это не идеальный полосовой фильтр, то добротность контура зависит от активного сопротивления катушки индуктивности r :
Q / r .
Входное сопротивление контура Z R |
|
/(1 j) , |
где |
Q( f / f |
рез |
f |
рез |
/ f ) – |
|||||
|
рез |
|
|
|
|
|
|
|
|
||||
обобщённая расстройка. При Q 1 , 2Q( f f |
рез |
) / f |
рез |
и | Z |
| R |
/ 0, 5 /( f f |
рез |
) . |
|||||
|
|
|
|
рез |
|
|
|
|
|
||||
Если LC-контур настроен на n-ю гармонику, |
то амплитуда напряжения |
|
и само |
||||||||||
напряжение на выходе резонансного контура будут равны |
|
|
|
|
|
|
|
|
|
||||
Uвых In Rрез ,
Преобразование частоты квазигармонических сигналов в нелинейных и параметрических цепях
Используя НЭ можно выполнить преобразование частоты квазигармонических сигналов. Для этого на его вход необходимо подать сумму входного квазигармонического сигнала uвх (t) U (t) cos(1t 1 ) и сигнала uг (t) Uг cos(гt г ) – гармоническое колебание заданной частоты, которое получают на выходе вспомогательного генератора – гетеродина:
u(t) Eсм U (t) cos(1t 1 ) Uг cos(г t г ) .
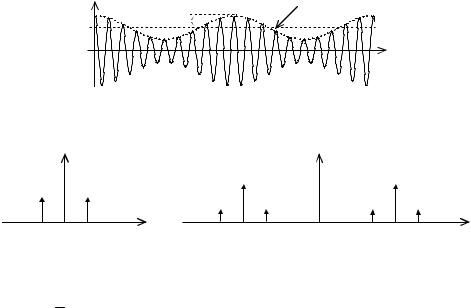
На выходе НЭ будет действовать ток, содержащий гармоники частоты входного сигнала 1 и сигнала гетеродина г , а также комбинационные частоты к | n1 1 n2 г | .
Настроив ПФ на частоту п | 1 г | или п 1 г , на выходе ПФ получим преобразованный сигнал uвых (t) kU (t) cos(пt п ) .
Преобразователь частоты производит транспонирование спектра узкополосного
сигнала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример. Если i = (u - E |
)2 , то |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i(t) |
1 |
U 2 (t) |
1 |
U 2 (t) cos 2 1t 21 U (t)Uг cos ( 1 г )t 1 |
г |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
||||||
|
U (t)Uг |
cos ( 1 г )t 1 г |
|
Uг2 |
|
U |
г2 cos 2 г t 2г . |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|||
|
Sвх,0 ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Sток,0 ( f ) |
|
|
|
|
|
|
f |
|
1 |
|
|
|
|
fг |
|
|
|
|
|
|
|
|
f |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fп fг f1 fг |
|
fг f1 |
|
|
|
2 fг |
f |
||||||||
|
Sвых,0 ( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
f |
|
п |
|
|
|
|
|
|
|
|
f |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Рис. 21. Спектры сигналов до и после преобразования частоты.
28
ЛЕКЦИЯ 7
Амплитудная модуляция (АМ) гармонических колебаний и её разновидности - балансная АМ (БАМ), АМ с одной боковой полосой (АМ ОБП). Спектры сигналов АМ при модуляции несущего колебания моногармоническим сигналом и случайным процессом. Особенности модуляции двоичными сигналами. Распределение мощности в АМ сигнале. Схемы модуляторов на нелинейных и параметрических элементах. Статическая модуляционная характеристика.
Вобщем виде сигнал АМ можно представить в виде произведения огибающей U (t) 0
ивысокочастотной гармонической несущей:
|
uАМ (t) U (t) cos(0t 0 ) , |
где 0 |
– частота несущей, 0 – начальная фаза несущей. |
Обычная АМ. При обычной АМ |
|
|
U (t) Um k x(t) |
и |
uАМ (t) (Um k x(t)) cos(0t 0 ) , |
где k – постоянный коэффициент, x(t) – модулирующий сигнал, Um – амплитуда несущей. При нормировании модулирующего сигнала b(t) x(t) / | x(t) |max
uАМ (t) Um 1 m b(t) cos(0t 0 ) ,
где m |
U |
|
k | x(t) |max |
– индекс амплитудной модуляции, 0 m 1 . |
||||||||||
Um |
|
|||||||||||||
|
|
Um |
|
перемодуляция, |
|
|
|
|
|
|
|
|||
При |
m 1 возникает |
в |
результате |
|
чего невозможно будет |
|||||||||
восстановить в приёмнике модулирующий сигнал без искажений. |
|
|
||||||||||||
При моногармоническом (однотональном) модулирующем сигнале x(t) U cos(t) |
||||||||||||||
|
|
|
|
|
|
|
b(t) cos( t) , |
|
|
|
|
|
|
|
|
|
|
uАМ (t) Um (1 m cos(t)) cos(0t 0 ) |
|
|
|||||||||
|
Um cos(0t 0 ) |
Umm |
cos((0 )t |
0 ) |
Um m |
cos(( |
0 |
)t 0 ) , |
||||||
|
|
2 |
|
2 |
|
|||||||||
где 2F . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
uАМ (t) |
|
|
U |
|
|
U (t) |
|
|
|
||
|
|
|
Um |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t
Рис. 22. АМ сигнал при моногармоническом модулирующем сигнале.
Спектр АМ сигнала при модуляции одним тоном изображен на следующем рисунке.
|
|
|
Sx ( f ) |
|
|
U m |
|
SАМ |
( f ) |
|
|
|
U m |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
U |
|
U |
|
|
|
2 |
|
U m m |
|
|
|
|
|
|
|
2 |
|
U m m |
|
|
|||
|
U m m |
|
|
|
|
|
U m m |
|
|
|
|
||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
4 |
|
|
4 |
|
||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
F |
0 F |
f |
|
|
|
|
0 |
|
f0 F |
f0 f0 F |
f |
||||||||||||
Рис. 23. Спектры сигналов до и после АМ при модуляции одним тоном.
Если модулирующий сигнал имеет более сложную форму, то его спектр равен
SАМ ( f ) 12 Um( f f0 ) Um( f f0 ) kSx ( f f0 ) kSx ( f f0 ) e j 0 .
29
