
ТЭЦ Лекции
.pdf1 /102
ТЭЦ часть I
Список литературы
1.Бакалов В. П., Дмитриков В. Ф., Крук Б. И Основы теории цепей. – М,: Радио и связь, 2000, – 592 с. – ЭВ
2.Белецкий А. Ф. Теория линейных электрических цепей. – М,: Радио и связь, 1986, – 543 с.
3. Атабеков Г. И. Теоретические основы электротехники. Линейные электрические цепи.
Часть 1, 2, 3. – М,: Энергия, 1978, – 592 с.
4.Попов В. П. Основы теории цепей. – М,: Высшая школа, 1985, 496 с (1998 2-е изд., 2000 3-е изд., 2003 4-е изд., 2006 5-е изд., 2007 6-е изд.) – 575 с.
5.Шебес М. Р. Теория линейных электрических цепей в упражнениях и задачах. – М,: Высшая школа, 1998, – 655 с.
6.Андреев В. С. Теория нелинейных электрических цепей. – М.: Радио и связь. 1982. –488 с. – ЭВ
7.Кушнир В. Ф., Ферсман Б. А. Теория нелинейных электрических цепей. – М.: Связь 1974. – 348 с. – ЭВ
8.Бакалов В. П., Крук Б. И., Журавлева О. Б. Теория электрических цепей. Новосибирск.
СибГАТИ, 1998, – 197 с.
9.Бакалов В. П., Игнатов А. Н., Крук Б. И. Основы теории электрических цепей и электроники. – М.: Радио и связь, 1989. – 528 с.
10.Зааль Р. Справочник по расчёту фильтров. – М.: Радио и связь. 1983. – 652 с.
11.Мошиц Г., Хорн П. Проектирование активных фильтров. – М.: Мир. 1984. – 320 с.
12.Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. – М.: Гардарики.
1999. – 638 с.
Список методических разработок |
|
|
1. |
Михайлов В. И., Чернышева Л. П. Методические указания к лабораторным работам по 1-й части |
|
|
курса “ Основы теории цепей”. ПГАТИ, каф. ТЭЦ, Самара, 2002, 85 с. – ЭВ, tors.psuti.ru |
|
2. |
Киреев В. Р., Грачев С. В., Михайлов В. И., Цаплин Н. Н. Методические указания |
к |
|
лабораторным работам по 2-й части курса ОТЦ. ПГАТИ, каф. ТЭЦ, Самара, 2000, 104 с. – |
ЭВ, |
tors.psuti.ru
3.Киреев В. Р., Крухмалёва В. Д., Михайлов В. И. Методические указания к лабораторным работам по 3 части курса ОТЦ. ПГАТИ, каф. ТЭЦ, Самара, 2001, 90 с. – ЭВ, tors.psuti.ru
4.Методические указания к контрольной работе № 1 по 1-й части курса “ Основы теории цепей” Составители: – к.т.н., доц. Михайлов В. И., к.ф-м.н. Панин Д. Н. – ЭВ, tors.psuti.ru
5.Методические указания к контрольной работе № 2 по 2-й части курса “ Основы теории цепей” Составители: – к.т.н., доц. Михайлов В. И., к.ф-м.н. Панин Д. Н. – ЭВ, tors.psuti.ru
7.Дубинин А. Е., Михайлов В. И., Киреев В. Р., Чернышева Л. П., Цаплин Н. Н. Основы теории цепей. Тестовые задания по курсу ОТЦ. ПГАТИ, кафедра ТЭЦ, Самара 2004,.58 с.
8.Методические указания к лабораторным работам по курсу ТЭЦ “ Исследование нелинейных цепей с помощью пакета Electronics Workbench”, кафедра ТЭЦ ПГАТИ. Составители: к.т.н., доц. Михайлов В. И., к.т.н., доц. Алексеев А. П., Самара, 2000.
9.Дубинин А. Е., Михайлов В. И., Цаплин Н. Н., Членова Е. Д. Расчет электрических фильтров по рабочим параметрам. Учебное пособие к курсовой работе, ГОУВПО ПГАТИ, Самара,2005.
10.Учебное пособие к курсовой работе по дисциплине Основы теории цепей «Проектирование электричексих фильтров» Составители: – к.т.н., доц. Михайлов В. И., к.ф-м.н.. Панин Д. Н. , кафедра ТОРС ПГАТИ., Самара, 2008. 46 с – ЭВ, tors.psuti.ru
Дополнительная литература
1. Атабеков Г. И. Теоретические основы электротехники. Линейные электрические цепи. Часть I. –
М,: Энергия, 1969, – 424 с. – ЭВ
2. Дезоер Ч. А., Ку Э. С. Основы теории |
цепей. Пер. с англ. Н. Л. Смирновой под ред. |
В. А. Смирнова. М., «Связь», 1976. 288 с. – |
ЭВ |
3. Шебес М. Р., Каблукова М. В. Задачник по теории линейных электрических цепей. Учеб. пособ. для электротехнич., радиотехнич. спец. вузов. 4-е изд., перераб. и доп. – М.: Высшая школа,
1990, – 544 с. – ЭВ
4. Шебес М. Р. Теория линейных электрических цепей в упражнениях и задачах. Учебное пособие для электротехнич., радиотехнич. специальностей вузов. – М.: Высшая школа, 1973,– 656 с. – ЭВ
|
|
2 |
/102 |
5. |
Белецкий А. Ф. Основы теории линейных электрических цепей. – М,: Связь, 1967, – 608 с. – ЭВ |
|
|
6. |
Карни Ш. Теория цепей. Анализ и синтез. Пер. с англ. |
Э. П. Горюнова, Е. А. Петрова, |
|
|
В. Г. Раутиана под ред. С. Е. Лондона. М., «Связь», 1973 г. – 368 |
с. – ЭВ |
|
7.Баскаков В. И. Радиотехнические цепи и сигналы. – М.: Высшая школа. 1988. –498 с.
8.Добротворский И. Н. Теория электрических цепей. Лабораторный практикум. М.: Радио и связь. 1990. –216 с.
9.Карлащук В. И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и её применение. – М.: Солон. 2000. –506 с.
10. Зевеке Г. В., Ионкин |
П. А., |
Нетушил А. В., Страхов С. В. Основы теории цепей. – М.: |
Энергоатомиздат. 1989. |
– 528 |
с. |
11.Ханзел Г. Е. Справочник по расчёту фильтров. – М.: Советское радио. 1974. –288 с.
12.Демирчан К. С., Бутырин П. А. Моделирование и машинный расчет электрических цепей. – М.: Высшая школа. 1988. –355 с.
13.Сборник задач по теории электрических цепей: Учеб. пособие для вузов / Данилов Л. В.,
Матханов П. Н., Мерзлютин Ю. Б. и др.; Под ред. Матханова П. Н. и Данилова Л. В. – М.: Высшая школа, 1980, – 224 с.
1 лекция
Задачи ОТЦ. Классификация электрических цепей и процессов в них. Понятие об электрических цепях.
Основная задача ОТЦ – изучение методов анализа и синтеза электрических цепей.
Задача анализа – расчёт электрических величин для заданной цепи.
Задача синтеза – создание электрической цепи с заданными свойствами.
Систему уравнений, описывающую модель электрической цепи, называют математической моделью цепи. В теории электрических цепей изучаются общие свойства моделей цепей, поэтому под электрической цепью понимают её модель, свойства которой близки к свойствам реальной физической цепи.
Классификация электрических цепей
Линейные и нелинейные цепи
Если цепь имеет линейную вольтамперную характеристику (не содержит нелинейных элементов), то такая цепь является линейной.
Если цепь имеет нелинейную вольтамперную характеристику (содержит хотя бы один нелинейный элемент), то такая цепь является нелинейной.
Активные и пассивные цепи
Активная цепь содержит хотя бы один активный элемент (например, источник тока или напряжения). Пассивная цепь не содежит активных элементов.
Параметрические и непараметрические цепи
Цепь, в которой один или несколько параметров изменяются во времени (но не зависят от входного сигнала) называется параметрической. Если цепь не содержит ни одного подобного элемента она являетс непараметрической.
Цепи с распределёнными и с сосредоточенными параметрами
В зависимости от соотношения между длинами самой цепи l и длиной волны тока и напряжения λ различают цепи с сосредоточенными и распределёнными параметрами. Если l < λ , считается, что параметры R (сопротивление), L (индуктивность) и C (ёмкость) сосредоточены в резисторах, катушках индуктивности и конденсаторах. При l λ необходимо пользоваться моделью цепи с распределёнными параметрами.
Основные определения ОТЦ: электрический ток и напряжение, мощность и энергия и единицы их измерения.
Электрическим током называют упорядоченное движение электрических зарядов под воздействием электрического поля.
Мгновенным значением тока i (t ) называют скорость изменения заряда q во времени:
i(t ) = lim |
q = |
d q |
, |
(1) |
|
||||
t→0 |
t dt |
|
||

|
|
|
3 |
/102 |
||
где q – электрический заряд, прошедший за время |
t через поперечное сечение проводника. |
|
|
|||
|
|
|
|
|
|
|
|
Обозначение |
Единица измерения в системе СИ |
Единица измерения сокращённо |
|
|
|
|
|
|
|
|
|
|
Электрический ток |
i |
Ампер |
|
А |
|
|
|
|
|
|
|
|
|
Электрический заряд |
q |
Кулон |
|
Кл |
|
|
|
|
|
|
|
|
|
Время |
t |
Секунда |
|
c |
|
|
|
|
|
|
|
|
|
Пусть имеется проводник (рис. а). Направление тока выбирается произвольно и указывается стрелкой. Ток i(t ), являющийся функцией времени, может принимать положительные и отрицательные значения.
|
|
a |
i(t) |
+ |
|
Электрическая |
|
i(t) |
u(t) |
|
|
|
|
||
|
|
− |
|
цепь |
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
b |
|
|
|
(двухполюсник) |
|
|
|
|
|
|
|||
а |
|
|
|
|
|
б |
|
Электрическое напряжение u (t ) между двумя точками a и b электрической цепи
определяется количеством энергии W, затрачиваемой на перемещение единичного заряда из точки a в точку b (рис б).
|
|
u (t ) = lim |
DW = |
d W |
. |
(2) |
|
|
|
||||
|
|
q→0 |
D q d q |
|
||
|
|
|
|
|||
|
Обозначение |
Единица измерения в системе СИ |
Единица измерения сокращённо |
|||
|
|
|
|
|||
Напряжение |
u |
Вольт |
В |
|||
|
|
|
|
|||
Энергия |
W |
Джоуль |
Дж |
|||
|
|
|
|
|
|
|
Положительное направление отсчёта напряжения (в каком направлении отсчитывается напряжение) u (t ) соответствует направлению перемещения положительно заряженных частиц от более высокого потенциала точки a к более низкому потенциалу точки b.
Электрическая энергия, затраченная на перемещение единичного заряда между двумя точками с напряжением u (t ) к моменту времени t определяется согласно (1) и (2) уравнением
q
W = ∫u (t )
0
t |
|
d q = ∫ u (t )i (t )d t . |
(3) |
−∞
Мгновенная мощность определяется производной энергии по времени:
|
|
p (t ) = |
d W |
= u (t )×i (t ) . |
(4) |
|
|
|
|
||||
|
|
|
d t |
|
||
|
|
|
|
|||
|
Обозначение |
Единица измерения в системе СИ |
Единица измерения сокращённо |
|||
|
|
|
|
|
|
|
Мощность |
p |
|
Ватт |
|
Вт |
|
|
|
|
|
|
||
Если p (t ) > 0 , |
то обусловлен |
процесс поглощения энергии, если p (t )<0 – |
процесс отдачи. |
|||
Электрическая цепь, её элементы и модели. Пассивные элементы.
Электрической цепью называют совокупность устройств, предназначенных для прохождения тока и описываемых с помощью понятий электрического тока и электрического напряжения. Электрическая цепь содержит в себе как источники, так и приёмники.
Источниками электрической цепи являются устройства, которые создают (генерируют) токи и напряжения.
Приёмниками электрической цепи называют устройства, потребляющие или преобразующие электрическую энергию в другие виды энергии.
В основе анализа электрических цепей лежит принцип моделирования: при анализе электрической цепи создаётся физическая модель, содержащая некоторую основную информацию об этой цепи. Далее формируется математическая модель – система уравнений, с помощью которых описывается физическая модель.
Пассивными элементами являются резистивное сопротивление, индуктивность и ёмкость.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
/102 |
|
Резистивным сопротивлением называют идеализированный элемент, обладающий |
|
|
||||||||||||||
свойством необратимого рассеивания энергии. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
R iR |
|
|
|
|
|
|
|
|
||||
Условное обозначение: |
|
|
uR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Математическая модель определяется законом Ома: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
uR = R iR , |
где G = |
1 |
, |
|
(5) |
|
|
|||
|
|
|
|
|
|
iR = G uR , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|||||
|
|
|
|
|
|
|||||||||||
|
Обозначение |
Единица измерения в системе СИ |
Единица измерения сокращённо |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сопротивление |
R |
|
|
|
|
|
Ом |
|
|
|
Ом |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проводимость |
G |
|
|
|
|
Сименс |
|
|
|
См |
|
|
|
|||
|
|
|
|
|
|
|
||||||||||
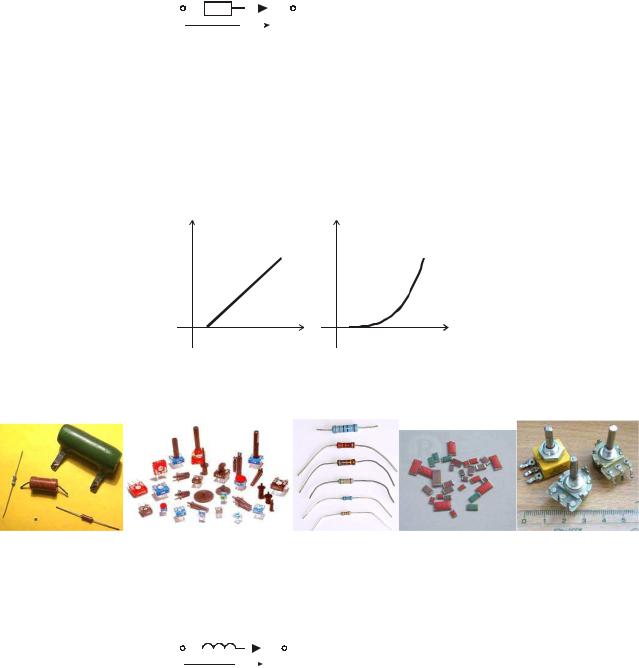
Уравнение (5) определяет вольт-амперную характеристику (ВАХ) резистивного элемента. |
|
|
|
|||||||||||||
|
|
i |
Линейная ВАХ |
i |
Нелинейная ВАХ |
|
|
|
||||||||
u |
u |
Мощность в резистивном сопротивлении определяется соотношением вида:
p |
= u |
R |
i |
= R i2 |
= G u2 . |
(6) |
R |
|
R |
R |
R |
|
Резисторы (радиоэлементы)
Индуктивным элементом называют идеализированный элемент, обладающий свойством накопления им энергии магнитного поля.
|
Обозначение |
Единица измерения в системе СИ |
Единица измерения сокращённо |
||||||
|
|
|
|
|
|
|
|
|
|
Индуктивность |
L |
|
|
|
|
Генри |
Гн |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L iL |
|
||||
Условное обозначение: |
|
|
uL |
|
|
|
|
|
|
|
|
||||||||
Математическая модель определяется соотношением вида: |
|
||||||||
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
Ψ = L iL , Ψ = ∑Φk , |
(7) |
||
|
|
|
|
|
|
|
|
k =1 |
|
|
Обозначение |
Единица измерения в системе СИ |
Единица измерения сокращённо |
||||||
|
|
|
|
|
|
|
|
||
Потокосцепление |
Ψ |
|
|
|
|
Вебер |
Вб |
||
|
|
|
|
|
|
|
|
||
Магнитный поток |
Ф |
|
|
|
|
Вебер |
Вб |
||
|
|
|
|
|
|
|
|
||
Число витков в катушке |
w |
|
|
|
|
– |
– |
||
индуктивности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (7) определяется вебер-амперную характеристику. Связь между током и напряжением на индуктивном элементе определяется согласно закону электромагнитной индукции выражением:
uL |
= |
d Ψ |
= L |
d iL |
. |
(8) |
d t |
|
|||||
|
|
|
d t |
|
||
Если через индуктивный элемент протекает постоянный ток, то напряжение будет равно нулю, что эквивалентно коротко замкнутому (КЗ) участку.

5 /102
|
|
|
|
Схема замещения |
|||||
L iL |
|
К. З. iL |
|||||||
uL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
uL= 0 |
|||||||
Мощность в индуктивном элементе определяется как:
p |
= u |
|
i |
= L i |
d iL |
. |
(9) |
|
|
||||||
L |
|
L |
L |
L |
d t |
|
|
Уравнение (9) показывает, что мощность может быть как положительной, так и отрицательной. Энергия, запасённая в индуктивном элементе к моменту t, определяется в виде:
t |
t |
d iL |
2 |
|
|
|
WL = ∫ |
pL d t = ∫ L iL |
d t = |
L iL |
. |
(10) |
|
d t |
|
|||||
−∞ |
−∞ |
2 |
|
|
||
|
|
|
|
|
||
Катушки индуктивности (радиоэлементы)
Ёмкостным элементом называют идеализированный элемент, обладающий свойством накапливать энергию электрического поля.
|
Обозначение |
Единица измерения в системе СИ |
Единица измерения сокращённо |
||||||
|
|
|
|
|
|
|
|
|
|
Ёмкость |
С |
|
|
|
|
|
Фарад |
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C iC |
|
|||||
Условное обозначение: |
|
|
uc |
|
|
|
|||
|
|
|
|||||||
Математическая модель определяется выражением вида: |
|
||||||||
|
|
|
|
|
|
|
|
q = C uC . |
(11) |
Уравнение (11) определяет вольт-кулонную характеристику. Связь между током и напряжением на ёмкостном элементе определяется как:
|
|
|
|
|
|
i |
= |
d q |
= C |
d uC |
. |
|
|
|
|
|
|
(12) |
|
|
|||||||||||||||||
|
|
|
|
|
|
C |
|
d t |
|
d t |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
При постоянном напряжении ток равен нулю, то есть ёмкостной элемент эквивалентен |
||||||||||||||||||
разрыву цепи или холостому ходу (ХХ). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
C iC |
|
|
|
|
Схема замещения |
|
|||||||||||
|
|
|
|
|
|
|
Х. Х. iC= 0 |
|
||||||||||
|
|
uc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uC |
|
||||||||
Мощность в ёмкостном элементе определяется как:
p |
= u |
|
i = C u |
|
d uC |
. |
(13) |
|
|
|
|||||
C |
|
C |
C |
C d t |
|
||
Из (13) видно, что мощность также может быть как положительной, так и отрицательной. Энергия, запасённая в ёмкостном элементе к моменту t:
t |
t |
d uC |
2 |
|
|
|
WC = ∫ |
pC d t = ∫ C uC |
d t = |
C uC |
. |
(14) |
|
d t |
|
|||||
−∞ |
−∞ |
2 |
|
|
||
|
|
|
|
|
||

6 /102
Конденсаторы (радиоэлементы)
Активные элементы. Независимые и зависимые источники.
Активными элементами являются зависимые и независимые источники энергии.
Кзависимым источникам относят: электронные лампы, транзисторы, операционные усилители.
Кнезависимым источникам относят: аккумуляторы, электрогенераторы, термоэлементы.
Независимые источники подразделяются на источники напряжения и источники тока.
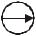
Независимым источником напряжения (ЭДС) называют идеализированный двухполюсник, напряжение, на зажимах которого не зависит от протекающего через него тока.
Eист
a −
− +
+  b
b
Условное обозначение: |
Uba |
Eист = Uba |
Внутреннее сопротивление идеального независимого источника напряжения (ЭДС) равно нулю. ВАХ такого источника представлена на рисунке:
i
Uab u
Реальный независимый источник напряжения (ЭДС) обладает внутренним сопротивлением:
UR |
Uист |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
a |
Rист U |
|
Eист |
b |
|
|
|
||||||
|
|
|
|
|
Uab |
|
|
|
|||||
|
|
|
|
|
ba |
|
|
|
= −Uab = Eист − Rист I , UR |
= Rист I , Eист = Uист |
|||
Условное обозначение: |
|
|
|
Uba |
|||||||||
|
|
|
|
|
|
|
|
||||||
ВАХ реального независимого источника напряжения:
|
i |
i |
|
|
|
|
|
−E |
α |
|
α |
|
uab |
E |
uba |
Тангенс угла пропорционален проводимости Gист = 1
Rист
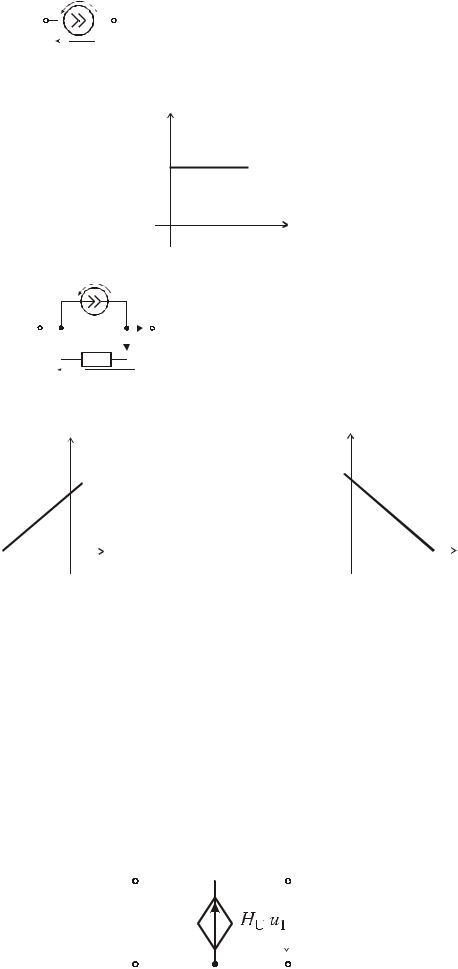
Независимым источником тока называют идеализированный двухполюсный элемент, ток которого не зависит от напряжения на его зажимах.
7 /102
UJ |
Jист |
||||||
|
|
|
|
|
b |
||
a |
|
|
|
|
|
|
|
Условное обозначение: Uba |
|
UJ = Uba |
|||||
ВАХ такого источника в виде сплошной линии. Внутреннее сопротивление равно бесконечности.
i
Jист
u
Реальный независимый источник тока обладает внутренней проводимостью
|
|
UJ |
Jист |
|
|
|
||
a |
|
I |
b |
|
|
|||
|
|
GистJист−I |
|
Gист = |
1 |
, UJ = Uba , Uba = Rист ( Jист − I ) |
||
|
|
|
||||||
|
|
|
||||||
Условное обозначение: |
Uba |
|||||||
|
||||||||
|
|
|
|
|
|
Rист |
||
ВАХ реального независимого источника тока: |
|
|
||||||
|
|
i |
|
|
|
|
i |
|
uba
|
|
|
RJист |
−RJист |
uab |
||
Возможен переход от схемы независимого источника напряжения (ЭДС) к эквивалентной схеме независимого источника тока по формулам:
J |
ист |
= |
Eист |
, E |
= |
Jист |
, R |
= |
1 |
. |
(15) |
|
|
|
|||||||||
|
|
|
ист |
|
|
ист |
|
Gист |
|
||
|
|
|
Rист |
|
Gист |
|
|
||||
Зависимый источник представляет собой четырёхполюсник с двумя парами зажимов: входных (1, 1’) и выходных (2, 2’). Различают четыре типа зависимых источников:
1.Источник напряжения, управляемый напряжением (ИНУН)
2.Источник напряжения, управляемый током (ИНУТ)
3.Источник тока, управляемый напряжением (ИТУН)
4.Источник тока, управляемый током (ИТУТ)
Входные ток i1 и напряжение u1 являются управляющими.
Покажем условные обозначения зависимых источников различного типа.
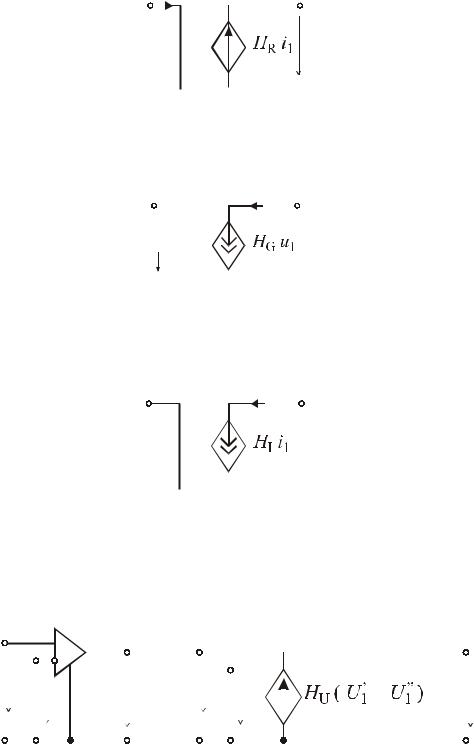
В ИНУН (рис. а) входное сопротивление равно бесконечности, входной ток равен нулю, а выходное напряжение связано с входным равенством вида: u2 = HU u1 .
1 |
|
|
|
|
2 |
|
|
|
|||
u1 |
|
|
u2 |
||
1’ |
|
|
|
|
2’ |
|
|
|
|
||
Рис. а. Коэффициент H U характеризует усиление по напряжению.
8 /102
В ИНУТ (рис. б) входным током i1 управляется выходное напряжение u2. Входная проводимость равна бесконечности, входное напряжение равно нулю.
i1
1 |
|
|
|
2 |
|
|
u2
1’

 2’
2’
Рис. б. Коэффициент HR имеет размерность сопротивления.
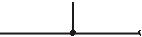
В ИТУН (рис. в) выходной ток i2 управляется входным напряжением u1. Входной ток равен нулю, входное сопротивление равно бесконечности.
i2
1 |
|
|
|
2 |
|
|
u1
1’
 2’
2’
Рис. в. Коэффициент HG имеет размерность проводимости.
В ИТУТ (рис. г) управляющим током является входной ток i1. Входная проводимость равна бесконечности.
i1 i2
1 |
|
2 |
|
1’

 2’
2’
Рис. г. Коэффициент HI характеризует усиление по току.
Примером зависимого источника является операционный усилитель (ОУ). Операционный усилитель имеет два входа: 1 – неинвертирующий и 2 – инвертирующий. Идеальный ОУ представляет собой ИНУН с бесконечно большим коэффициентом усиления H U , с бесконечно
большим входным сопротивлением и выходной проводимостью.
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
1 + |
|
|
|
|
|
|
|
|
+ |
|
|
||||||
|
|
2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
U’ |
|
|
|
|
U |
2 |
|
|
U’ |
|
2 + |
|
|
|
|
|
U |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
U1’’ |
|
|
|
|
|
|
|
U1’’ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
− |
|
− |
|
|
− |
|
|
− |
|
|
− |
|
|
|
|
− |
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Электрическая схема. Топология электрической цепи.
Электрической схемой называют графическое изображение электрической цепи. Микросхемой (интегральной схемой) называют интегральную электрическую цепь, содержащую сотни и тысячи простейших активных и пассивных элементов.
Для анализа электрических цепей в последнее время применяют топологические методы, заключающиеся в представлении электрической цепи в виде графа. Граф – геометрическая система линий (ветвей), соединяющих заданные точки (узлы). Граф, у которого ветви ориентированы по направлению токов ветвей, является направленным (ориентированным). Пусть дана электрическая схема в виде:

9 /102
|
|
|
1 |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
i1 |
|
|
|
L3 i3 |
|
|
|
|
|||
e(t) |
|
|
|
|
|
|
|
|
R4 |
|
C5 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
i5 |
|
|
|
i2 |
|
i6 |
|
|
|
|
i4 |
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
R6 |
|
|
|
|
|||
|
|
|
3 |
4 |
|
|
|
|||||
Для этой цепи ориентированный граф будет выглядеть следующим образом:
1 |
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
Основные понятия и определения в топологии цепей:
1.Узел – место соединения зажимов трёх и более элементов.
2.Ветвь – часть цепи, включаемой между двумя узлами, через которые она обменивается энергией с остальной цепью.
3.Путь – последовательно соединенные ветви цепи.
4.Контур – замкнутый путь.
Законы Ома и Кирхгофа.
Георг Симон Ом (Georg Simon Ohm), 1787-1854, |
Густав Роберт Кирхгоф (Gustav Robert Kirchhoff), |
немецкий физик |
1824-1887, немецкий физик |
Закон Ома применяется для ветви или для одноконтурной замкнутой цепи. При написании закона Ома следует выбрать произвольно положительное направление тока.
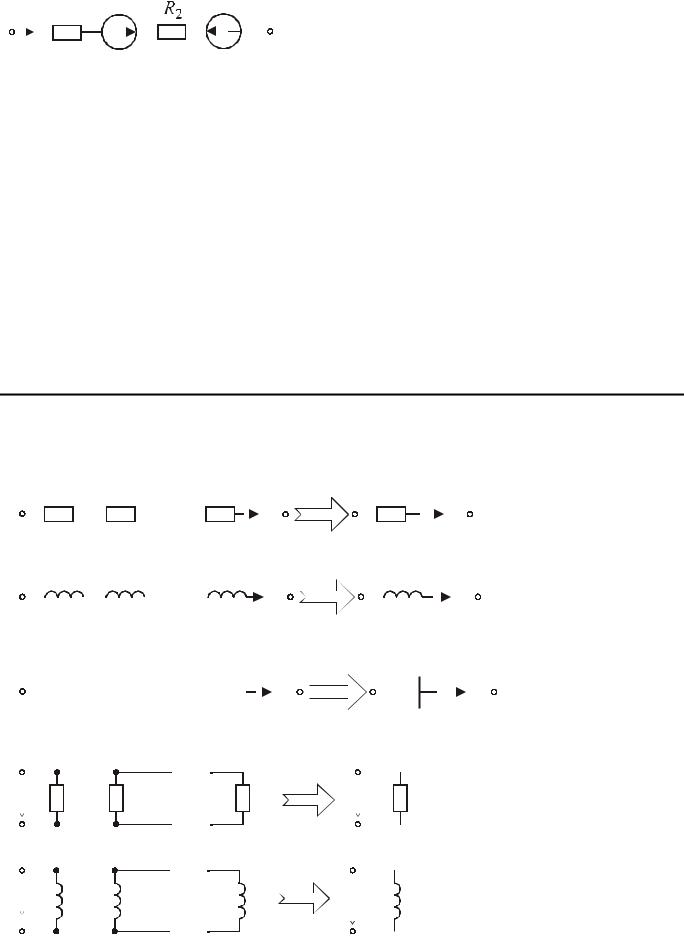
1. Закон Ома для ветви, состоящей только из резисторов:
|
I |
R1 |
|
Va −Vb |
|
|
|
|
||||||||
a |
|
|
|
|
|
|
|
|
|
b |
I = |
= |
Uab |
. |
(16) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|||
∑ Rn Rab
n=1
2. Закон Ома для ветви, содержащей источники ЭДС и резисторы:
10 /102
|
|
|
E1 |
|
|
|
E2 |
|
|
|
|
|
|
|
||||||
|
I R1 |
|
|
|
|
|
|
|
|
|
|
Va −Vb + E1 − E2 |
|
|
||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
I = |
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 + R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I = |
Va −Vb |
+ ∑ E |
|
||||
В общем случае: |
|
|
|
|
|
|
|
|
|
. |
|
(17) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ Rab |
|
||||
Для замкнутого контура: |
|
|
|
|
|
|
|
I = |
∑ E |
(18) |
||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ R |
|
||||
|
I закон Кирхгофа – |
алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ Ik = 0 . |
(19) |
||||
k=1
IIзакон Кирхгофа – алгебраическая сумма ЭДС замкнутого контура равна алгебраической сумме падений напряжений на нём.
n
∑ Ek
k =1
n |
|
= ∑ Rk Ik . |
(20) |
k =1
Направление обхода контура выбирают произвольно. В левой части (20) ЭДС, направления которых совпадают с направлением контура принимаются положительными. При записи правой части равенства (20) со знаком «+» берутся падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с направлением обхода контура.
Принцип эквивалентности. Преобразование схем.
Принцип эквивалентности: n напряжения и токи в ветвях схемы, не затронутых преобразованием, остаются неизменными.
Последовательное соединение элементов:
1. Последовательное соединение резистивных элементов:
|
|
|
R1 |
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RN |
iR |
|
|
|
|
|
|
|
Rэкв |
iR |
|
|
|
|
|
|
|
|
N |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rэкв |
= ∑ Rn . |
(21) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
2. Последовательное соединение индуктивных элементов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
L1 |
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LN |
iL |
|
|
|
|
|
|
|
|
Lэкв |
|
iL |
|
|
|
|
|
|
|
|
N |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lэкв |
|
= ∑ Ln . |
(22) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
||
3. Последовательное соединение ёмкостных элементов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
C1 |
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CN |
iC |
|
|
|
|
|
|
|
|
|
|
|
Cэкв iC |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
N |
1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑ |
. |
(23) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cэкв |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
Cn |
|
||||||
|
|
Параллельное соединение элементов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
1. Параллельное соединение резистивных элементов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
uR |
|
|
R1 |
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RN |
|
|
|
uR |
|
|
|
|
Rэкв |
|
N |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑ |
|
|
. |
|
|
(24) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rэкв |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 Rn |
|
|
|
|
|
||||||||
2. Параллельное соединение индуктивных элементов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
u |
|
|
L1 |
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LN |
|
u |
L |
|
|
Lэкв |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
N |
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑ |
|
. |
|
|
(25) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lэкв |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 Ln |
|
|
|
|
|
|||||||
3. Параллельное соединение ёмкостных элементов:
