ТЭЦ Лекции

iL (0− ) = iL (0) = 0 , uC (0− ) = uC (0) = 0 –

задача с нулевыми начальными условиями.

Схема цепи после коммутации

K

uR(t)

i(t)

u

(t ) + u

(t ) + u

(t ) = Ri

(t ) + L

diL (t )

+ u

(t ) = E , так как i

(t ) = i

(t ) = i

(t ) = C

duC

, то

R

L

C

C

R

dt

L

C

R

dt

LC

d 2uC (t )

+ RC

duC (t )

+ uC (t ) = E – НДУ.

dt 2

dt

uCпр

uCпр = lim uC (t ) = E .

t

→∞

Определяем свободную составляющую:

LC

d 2uCсв (t )

+ RC

duCсв (t )

+ uCсв (t ) = 0 – ОДУ; LCp

2

+ RCp +1

= 0 –

характеристическое уравнение.

dt

2

dt

p

= −

R

±

R

2 −

1

– корни характеристического уравнения.

1, 2

2L

LC

2L

Rкр 2

1

= 0 , откуда Rкр = 2

L

= 2ρ . Здесь ρ –

−

характеристическое сопротивление контура.

2L

LC

C

Если R > R = 2

L

, то имеет место апериодический процесс.

кр

C

Свободная составляющая определяется u

Cсв

(t ) = A e p1t + A e p2t .

1

2

Общий вид реакции: u

C

(t )

= A e p1t + A e p2t + E .

1

2

Для определения A1 и A2 составим ещё одно уравнение:

duC (t )

= A1 p1e p1t

+ A2 p2e p2t , поскольку iL (t ) = iC (t ) = C

duC

, то iL (t ) = C ( A1 p1e p1t + A2 p2e p2t ) .

dt

dt

82

/102

Определим постоянные интегрирования из начальных условий: iL (0) = 0 , uC (0) = 0 .

При этом, образуется система алгебраический уравнений:

A1 + A2 + E = 0,

=

Ep

2

, A2

= −

Ep

.

A1 p1 + A2 p2 = 0,

откуда A1

1

p1

p1

− p2

− p2

После подстановки и алгебраических преобразований получим:

uC (t ) = E +

E

( p2e p1t

− p1e p2t ) – переходное напряжение на ёмкости.

p − p

1

2

iL (t ) =

E

)

(e p1t

− e p2t ) – переходной ток в индуктивности.

− p

L ( p

2

1

uL (t ) = L diL (t ) =

( p

E

)

( p1e p1t − p2e p2t )

–

переходное напряжение на индуктивности.

dt

− p

2

1

uR (t ) = iR (t ) R =

ER

(e p1t − e p2t ) –

переходное напряжение на резисторе.

L ( p − p

)

2

1

u(t)

E

0

t

t =

1

ln

p2 , t

2

= 2t .

1

p1

− p2

p1

1

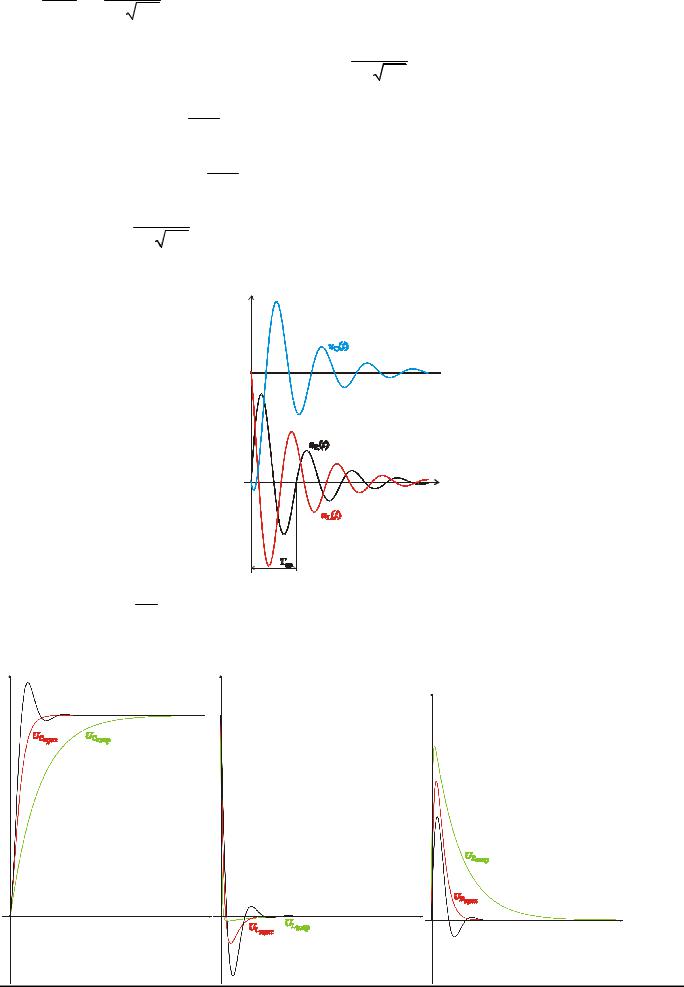
Включение последовательной RLC-цепи на постоянное напряжение. Критический

процесс.

Если R = R

= 2

L , то имеет место критический процесс.

кр

C

Свободная составляющая определяется u

Cсв

(t ) = (

A + A t ) e pt .

1

2

Общий вид реакции: u (t ) =

( A + A t ) e pt + E , где p = p = p

= −

R

.

2

C

1

2

1

2L

Для определения A1 и A2 составим еще одно уравнение:

duC (t )

= A e pt + p ( A + A t )e pt , поскольку i

(t ) = i

(t ) = C

duC

, то

dt

2

1

2

L

C

dt

iL (t ) = C ( A2e pt

+ p ( A1 + A2t )e pt ) , так как iL (0) = 0 , uC (0) = 0 получаем систему:

A1 + E = 0,

откуда A1 = −E , A2 = pE .

A2 + pA1 =

0,

i

(t ) =

E

te pt –

переходной ток в индуктивности. Доказать самостоятельно!

L

L

uL

(t ) = L

diL (t )

= L

E

(e pt + tpe pt ) = E (1+ pt )e pt – переходное напряжение на индуктивности.

dt

L

u

(t ) = i

(t ) R =

ER

te pt – переходное напряжение на резисторе.

R

R

L

R

1

R 2

2

2

p1, 2 = −

± j

−

= −σ ± j ω0

− σ

= −σ ± jωсв ,

LC

2L

2L

R

1

R

2

1

2

2

где σ =

, ωсв =

−

= ω0 − σ

,

ω0 =

.

LC

2L

2L

LC

Решение определяем в виде: u

C

(t ) = Ae−σt sin (ω t + ψ) + E , здесь

св

ωсв

– угловая частота свободных (собственных) колебаний;

σ –

показатель затухания контура;

1

–

постоянная времени колебательного контура.

σ

0

= Asin ψ + E,

ωсв

, A = −

E

= CA(ω cos ψ − σ sin ψ ),

ψ = arctg

σ

.

0

sin ψ

св

Поскольку ωсв cos ψ − σ sin ψ = 0 , то ωсв

1− sin2 ψ

= σ sin ψ , ωсв2

(1− sin2 ψ) = σ2 sin2 ψ .

После преобразований получим уравнение: ωсв2 = (σ2 + ωсв2 ) sin

2 ψ , откуда sin ψ =

ωсв

.

σ2 + ωсв2

ωсв

ωсв

ωсв

Последнее выражение приведем к виду:

=

=

, следовательно

ω0

σ2 + ω2

σ2 + ω2 − σ2

св

0

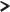
84

/102

A = −

E

= −

E

, ωсв = ω0 sin ψ , σ = ω0 cos

ψ .

sin ψ

ωсв

LC

1

ω

;

Переходное напряжение на ёмкости: uC (t ) = E 1−

ω

e−σt sin (ωсвt

+ ψ )

, где ψ = arctg

св

LC

σ

св

i (t ) =

E

e−σt sin ω t

–

переходный ток в индуктивности;

L

ωсвL

св

u

R

(t ) = i

(t ) R =

ER

e−σt sin ω

t

– переходное напряжение на резисторе;

L

ωсвL

св

u

L

(t ) = −

E

e−σt sin (ω t − ψ)

–

переходное напряжение на индуктивности.

ωсв

LC

св

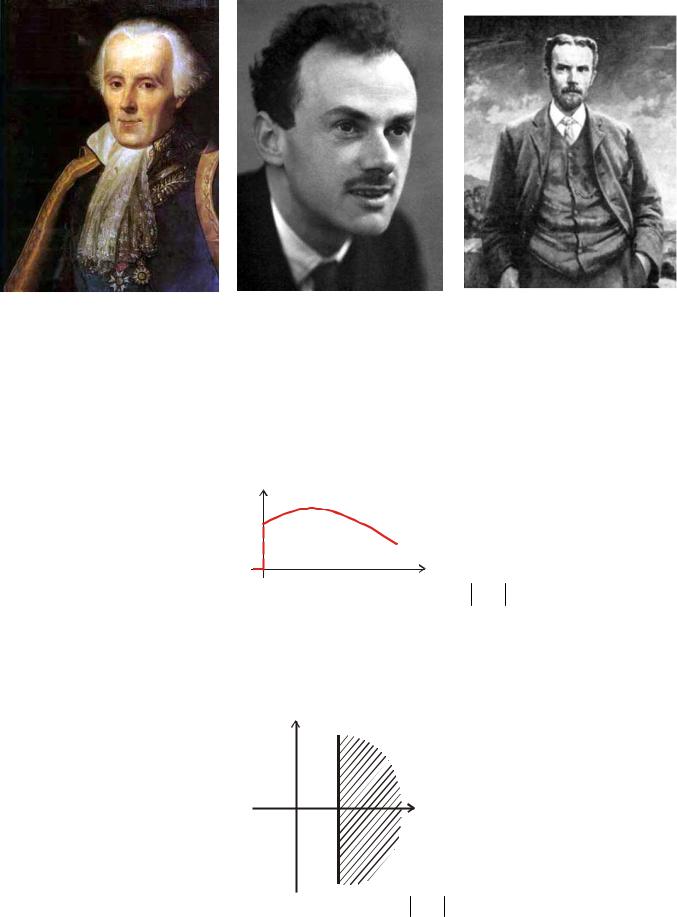
Представим на графике соответствующие переходные напряжения:

u(t)

E

0

t

Квазипериод: T

= 2π

.

Декремент затухания:

= eσTсв .

св

ωсв

Логарифмический декремент затухания: δσ = ln

= σTсв .

UC

UL

UCколеб

UR

t

t

t

URколеб

ULколеб

Пьер-Симо&нЛапла&с(Pierre-Simon

Поль Адриен Морис Дира&к(Paul

О&ливерХе&висайд(Oliver

Laplace), 1749-1827, французский

Adrien Maurice Dirac), 1902-1984

Heaviside), 1850-1925 английский

математик, физик и астроном

английский физик-теоретик

учёный-самоучка, инженер,

математик и физик

Операторный метод анализа переходных процессов. Преобразования Лапласа

В основе операционного метода расчёта переходных процессов лежит преобразование

Лапласа, которое позволяет перенести решение из области функций действительного переменного

t в обрасть комплексного переменного p = σ + jω .

При этом операции дифференцирования и интегрирования функций времени заменяются

соответствующими операциями умножения и деления функций комплексного переменногона

оператор p, что существенно упрощает расчёт, так как сводит систему дифференциальных

уравнений к системе алгебраических. В операторном методе отпадает необходимость определения

постоянных интегрирования.

(t )

Рассмотрим кусочно-непрерывную однозначную функцию f

f(t)

0

t

f (t ) dt < ∞ .

Пусть эта функция удовлетворяет условиям:

f (t ) = 0 , если t < 0 и ∫

Прямым преобразованием

Лапласа

F ( p)

функции

f (t )

является функция комплексной

∞

переменной вида: F ( p ) = ∫ f

(t )e− pt dt .

0

Интеграл такого типа абсолютно сходится в полуплоскости Re p = σ > σ0

Im

0

σ0

Re

f (t ) удовлетворяет условию ограниченного роста, то есть

f (t ) < Meσot , где M – множитель, σ0 –

показатель роста – положительные действительные числа;

f (t ) – оригинал, F ( p) – изображение

по Лапласу. Функция имеет ограниченный рост, если показатель роста конечен.

Для сокращения записи

преобразований используем:

f

(

t

) i

(

p

)

,

i

– знак

= F

где =

i

i

соответствия между оригиналом

f (t ) и его изображением

F ( p) ,

то

есть

парой

функций

1

σ+ j∞

Обратное преобразование Лапласа (Формула Римана-Меллина): f (t ) =

∫ F ( p)e pt dp

2πj

σ− j∞

∞

представляет собой решение интегрального уравнения F ( p ) = ∫ f (t )e− pt dt

относительно функции

0

точки p1 , p2 ,..., pk

плоскости комплексного переменного, в которых подинтегральная функция

1

σ+ j∞

выражения f (t ) =

∫ F ( p) e pt dp обращается

в бесконечность. Вычисление интеграла при

2πj

σ− j∞

этом сводится к определению

суммы вычетов

(обозначаемых буквами res ) подинтегральной

1

n

функции в полюсе

F ( p )e pt dp = ∑ resk (F ( p) e pt )

2πj ∫

k =1

Мари&Энмо&нКами&ль(Камилл)

Томас Джон Иансон Бромвич

Ви&кторВлади&мировичВа&гнер

Жорда&н(Marie Ennemond

(Thomas John I'Anson

1908-1981, советский математик

Camille Jordan, 1838-1922,

Bromwich) 1875-1929,

французский математик

английский математик