Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТЭЦ Лекции

.pdf

Скачиваний:

112

Добавлен:

10.06.2015

Размер:

2.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

91 /102

	I1(p)		I2(p)
U1(p)		Четырёх-		U2(p)
		полюсник
		полюсник

KU ( p) =	U2	( p)	, KI ( p) =		I2	( p )	, KZ ( p)
	U1	( p)			I1
						( p )
Представим ОПФ в виде:
K ( p) =		an pn + an−1 pn−1 +…+ a1 p + a0

		b pm + b		pm−1 +…+ b p + b
		m	m−1			1 0

( p)

, KY ( p) =

( p )

( p)

W ( p )

( p - p01 )( p - p02 )…( p - p0n )

, либо

K ( p) = H ( p - p )( p - p

)…( p - p

)

V ( p )

где p	, p	, …, p	– нули, p ,	p , …, p		– полюса ОПФ; H =	an	.
					m
01	02	0n	1	2			bn

Свойства ОПФ

1.ОПФ является дробно-рациональной функцией с вещественными коэффициентами

2.Полюсы ОПФ располагаются в левой полуплоскости комплексной переменной p.

3.Степень полинома числителя ОПФ не превышает степень полинома знаменателя. Пример

u1(t)

(t)

U2(p)

( p)

U1 ( p)

U1(p)

pС

KU ( p) =

( p)

pC U1

1+ pRC

Самостоятельно определить! KI ( p ),

KZ ( p),

KY ( p )

Для определения KI ( p) и KY ( p ) необходимо замкнуть накоротко выходные зажимы.

Временной метод анализа переходных процессов. Переходная и импульсная характеристика электрической цепи

Переходной характеристикой h (t ) называется реакция линейной электрической цепи на входное воздействие в виде функции Хевисайда.

1(t)

ЛЭЦ

h(t)

U1(p)

ЛЭЦ

U2(p)

( p)

KU ( p) =

, откуда U2 ( p) = KU ( p)U1 ( p) = KU ( p)

, откуда

( p)

i KU ( p )

(t ) =

– переходная характеристика по напряжению.

( p)

KZ ( p)

KY ( p)

i KI

(t ) =

Импульсной характеристикой

g (t )

называется реакция линейной электрической цепи на

входное воздействие в виде δ -функции Дирака.

92 /102

δ(t)

ЛЭЦ

g(t)

U1(p)

ЛЭЦ

U2(p)

KU ( p) =

( p)

, откуда U2 ( p) = KU ( p)U1 ( p) = KU ( p )×1 , откуда

( p)

(t ) = K

( p) –

импульсная характеристика по напряжению.

( p ) , g (t )

= K ( p)

g (t ) = K ( p) , g (t ) = K

Поскольку d(t ) =

d1(t )

, то g (t ) =

dh (t )

(h (t )1(t )) =

d1(t )

h (t ) +1(t )

dh (t )

= d(t ) h (t ) +

dh (t )

Учитывая фильтрующее свойство δ -функции d(t ) h (t ) = d(t ) h (0) , получим:

g (t ) = δ (t ) h (0) +

dh (t )

– связь между импульсной и переходной характеристикой.

Пример

h(t)

1(t)

U1(p)

U2(p)

pС

KU ( p )

Поскольку K

( p) =

, то h

(t ) =

+ pRC

p(1+ pRC)

Определим оригинал по теореме разложения:

F ( p ) =

( p)

–

изображение.

( p )

p(1+ pRC)

Корни полинома знаменателя:

p = 0 ,

p = -

Определим производную: (F2 ( p))¢ = 2 pRC +1 , причём (F2 ( p1 ))¢ = 1,

(F2 ( p2 ))¢ = -1 .

Переходная характеристика по напряжению: h (t ) =

−

e0t +

= 1- e τC , где t

= RC .

(-1)

gu (t ) = hu (0)d(t ) +

dhu (t )

e−

Импульсная характеристика по напряжению:

τC

Интеграл Дюамеля

Жан Мари Констан Дюамель

Другое имя:

Жан Мари Констант Дюгамель

(Jean Marie Constant Duhamel), 1797-1872,

французский математик.

Интеграл Дюамеля может быть получен, если аппроксимировать приложенное воздействие f1 (t ) с помощью единичных функций, сдвинутых относительно друг друга на время Δτ .

93 /102

	f1(t)	fk
		fk
	f2
	f1
f1(0)
0	Δτ 2Δτ	kΔτ	t

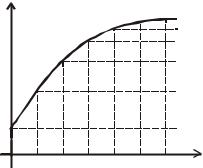
Реакция цепи на каждое ступенчатое воздействие определится как

f2 (0) = f1 (0) h (t ) ,

f2 (Δτ) = f1h (t − Δτ),

f2 (kΔτ) = fk h (t − kΔτ).

Результирующая реакция согласно принципу наложения: f2 (t ) = f2 (0) + ∑ f2 (kΔτ) , то есть

k =1

f2 (t ) = f1 (0) h (t ) + ∑ fk h (t − kΔτ) ,

k =1

где n –

число аппроксимирующих участков, на которые разбит интервал 0…t . Домножив и

разделив на Δτ перейдём пределу, где Δτ → 0 :

f2 (t )

= f1

(0) h (t ) + lim

h (t − kΔτ) Δτ .

∑

Δτ→0

k =1

Δτ

В этом случае kΔτ → τ , а lim

= f

′ ( τ) , сумма заменяется интегралом и в итоге получаем

Δτ→0

Δτ

f2 (t ) = f1 (0) h (t ) + ∫ f1′(τ) h (t − τ) d τ –

I форма интеграла Дюамеля.

Вторая форма интеграла Дюамеля получается с помощью теоремы свёртки

Если

f (t ) = F ( p) , то

(t − τ) f

(τ) d τ = F

f (τ) f

(t − τ) d τ .

( p ) F ( p) =

∫ 1

i 1

i ∫

f2 (t ) = f1 (0) h (t ) + ∫ f1′(t − τ) h (τ) d τ

–

II форма интеграла Дюамеля.

Интегрируя по частям, получим:

f2 (t ) = f1 (

0) h (t ) + ∫ f1

(τ) h′(t − τ) d τ

–

III форма интеграла Дюамеля.

f2 (t ) = f1 (

0) h (t ) + ∫ f1

(t − τ) h′(τ) d τ

–

IV форма интеграла Дюамеля.

Практический выбор формы интеграла Дюамеля определяется из соображений простоты вычисления подынтегральных выражений.

Рассмотрим применение интеграла Дюамеля для расчёта переходных процессов при произвольных воздействиях.

94 /102

f1(t)

f11(t) f1(0)

0	t1	t2	t
		F2

Выделяем следующие интервалы

1. t < 0 , f2 (t ) = 0 .

2. 0 ≤ t ≤ t1 , f2 (t )

= f1 (0) h (t )

+ ∫ f11 '(τ) h (t − τ) d τ .

3. t < t < t

)

= f

)

(

)

(

t − τ

)

d τ + F h

(

t − t

' τ

)

(

t − τ

)

d τ .

f ' τ

∫

(

1 (

∫ 11 (

1 )

22 (

t2 < t < ∞ ,

)

= f

)

(

)

(

t − τ

)

d τ + F h

(

t − t

' τ

)

(

t − τ

)

d τ − F h

(

t − t

2 )

'τ

)

(

t − τ

)

d τ

f ' τ

∫

(

1 (

∫ 11

(

1 )

22 (

33 (

Интегрирующие и дифференцирующие цепи

f (t)

ЛЭЦ

f2(t)

(t ) =

df1 (t )

–

дифференцирующая цепь;

f2 (t )

= ∫ f1 (t ) dt

–

интегрирующая цепь;

Дифференцирующие цепи

i(t) R

u1(t)

u2(t)

(t ) = L

di (t )

–

выходное напряжение

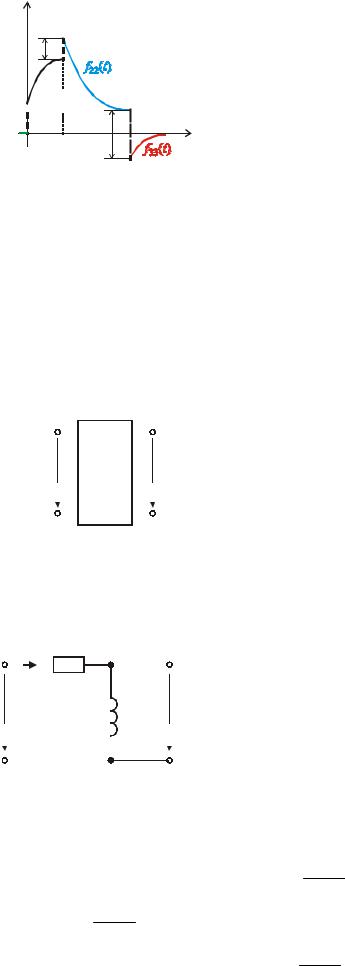
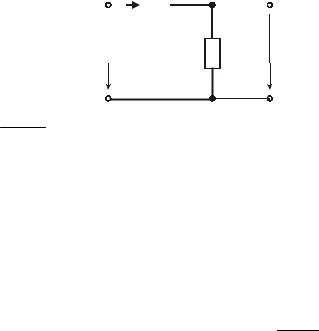
Запишем уравнение Кирхгофа в операторной форме:

U1 ( p) = I ( p ) R + I ( p) pL = UR ( p ) + UL ( p) , потребуем

чтобы UR ( p ) UL ( p) , то есть R pL , тогда U1 ( p ) ≈ I ( p) R , откуда I ( p) ≈ U1 ( p) .

U2 ( p) = I ( p) pL = U1 ( p) pL = τL pU1 ( p ) . R

На основании теоремы о дифференцировании оригинала получаем: u2 (t ) = τL du1 (t ) . dt

u2 (t ) = Ri (t ) = RC

95 /102

i(t)	С
i(t)	С
		R
u1(t)		R	u (t)
			2

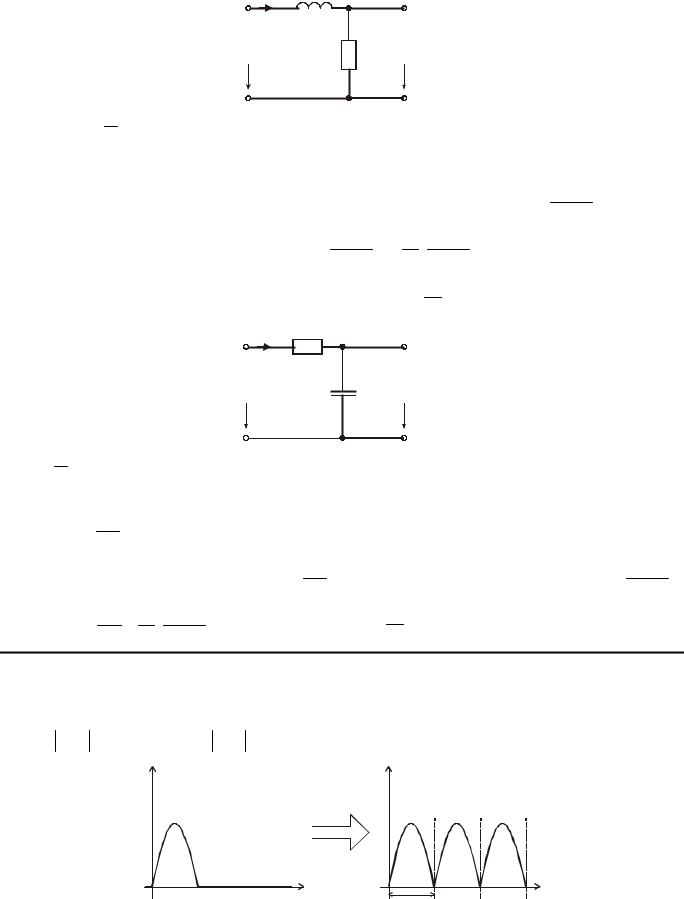
duC (t ) . dt

Запишем уравнение Кирхгофа в операторной форме:

U1 ( p ) = I ( p )	1	+ I ( p) R = UC ( p) + UR ( p ) .
U1 ( p ) = I ( p )		+ I ( p) R = UC ( p) + UR ( p ) .
	pC
Потребуем чтобы UR ( p) UC ( p) , то есть R			1	, тогда U1	( p) ≈ I ( p )	1	, откуда
Потребуем чтобы UR ( p) UC ( p) , то есть R			pC	, тогда U1	( p) ≈ I ( p )		, откуда
I ( p) ≈ pCU1 ( p ) .			pC			pC
I ( p) ≈ pCU1 ( p ) .

U2 ( p) = I ( p) R = pRCU1 ( p) = τC pU1 ( p ) .

Оригинал выходного напряжения определяется: u2 (t ) = τC du1 (t ) . dt

96 /102

Интегрирующие цепи

i(t)

u1(t)

u2(t)

(t ) = Ri (t ) = R

t uL (t ) dt .

∫

U1 ( p) = I ( p ) R + I ( p) pL = UR ( p ) +UL ( p) , потребуем

чтобы UL ( p) UR ( p) , то есть pL R , тогда U1 ( p) » I ( p ) pL , откуда I ( p) » U1 ( p) .

U2 ( p) = I ( p) R = U1 ( p) R =

1 ×U1 ( p) .

На основании теоремы об интегрировании оригинала u

(t ) =

u (t ) dt .

∫0

i(t)

u1(t)

u2(t)

(t ) = 1

t i (t ) dt .

∫

Запишем уравнение Кирхгофа в операторной форме:

( p ) = I ( p ) 1 + I ( p) R = UC ( p) +UR ( p ) .

( p ) » I ( p) R , откуда I ( p) » U1 ( p) .

Потребуем чтобы UC ( p) UR ( p) , то есть

R , тогда U1

( p) = I ( p) 1

= 1 ×U1 ( p) , откуда оригинал u

(t ) =

(t ) dt .

tC ∫0

Частотный метод анализа переходных процессов. Преобразования Фурье

Пусть f (t ) – непериодическая

функция,

удовлетворяющая

условию

абсолютной

интегрируемости в бесконечных пределах, то есть

∞

(t ) dt < ¥ , при этом f (t ) < Me−ct .

∫ f

−∞

f(t)

f1(t)

Представим f (t ) в виде бесконечно большого числа малых периодических функций f1 (t ) ,

то есть f (t ) = lim f1 (t ) .

T →∞

97 /102

f1 (t ) представим в виде комплексного ряда Фурье:

∞

2π

f1 (t ) =

∑ Ak ejkω1t , где Ak

∫ f1 (t )e− jkω1t dt , T =

k =−∞

−

в f1 (t ) ,

и переходя к пределу T → ∞ , учитывая, что kω1 → ω ,

Осуществляя подстановку Ak

ω1 → dω , получаем:

∞

f (t ) =

∫ F (ω) ejωt dω –

ОПФ, F (

ω) = ∫ f (t )e− jωt dt – ППФ.

2π

−∞

F (ω) –

комплексная спектральная плотность, а

F (ω)

= F (ω) – спектральная плотность.

F (ω) = A(ω) − jB (ω) = F (ω)e− jφ(ω) ,

F (ω) –

амплитудный спектр, φ(ω) – фазовый спектр.

Функцию f (t ) можно представить в другой форме:

	1	∞			1	∞		1	∞
f (t ) =	1	∫ F (ω)e− jφ(ω)ejωt dω =			1	∫	F (ω)cos (ωt − φ (ω))dω − j	1	∫ F (ω)sin (ωt − φ (ω))dω .
f (t ) =	2π	∫ F (ω)e− jφ(ω)ejωt dω =			2π	∫	F (ω)cos (ωt − φ (ω))dω − j	2π	∫ F (ω)sin (ωt − φ (ω))dω .
	2π	−∞			2π	−∞		2π	−∞
		−∞		∞		−∞			−∞
			1	∞
Окончательно		f (t ) =	1	∫ F (ω)cos (ωt − φ			(ω))dω .
Окончательно		f (t ) =	π	∫ F (ω)cos (ωt − φ			(ω))dω .
			π	0
				0

Вывод: непериодический сигнал может быть представлен пределом суммы (интегралом)

бесконечно большого числа бесконечно малых гармонических колебаний с амплитудами F (πω) и

начальными фазами φ(ω) . Спектры непериодических сигналов являются непрерывными.

Свойства преобразования Фурье

Джон Уильям Стретт, третий барон Рэлей, Лорд

Рэлей (Рэйли) (John Strutt, 3rd Baron Rayleigh), 1842-1919, британский физик

									∞
1.	Если f (t ) – чётная функция, то спектр F (ω)			–	действительный. F (ω) = ∫ f (t )cos ωtdt .
						∞			−∞
						∞
2.	Взаимозаменяемость переменных t	и ω . F (−t )			= ∫ f (ω)e jωt dω .
			∑ k			−∞
3.	i		∑ k			i ∑	a	k	F (ω) ,
3.	Теорема линейности. Если f (t ) = F (ω) , то			a		f (t ) =	a		F (ω) ,
	i					i
			k			k

где = – знак соответствия между сигналом и его спектром, определяемого парой преобразований

Фурье.

4. Теорема о дифференцировании сигнала. Если

(

)

(

)

, то

(

)

(

)

= F

= jωF

5. Теорема об интегрировании сигнала. Если

(

) i

(

)

, то

∫

(

)

(

)

= F

dt =

jω

−∞

f (t ) = F (ω) , то

= F (ω)e

6. Теорема запаздывания (опережения). Если

f (t ± t )

± jωt0

98 /102

7. Теорема сжатия. Если

f (t ) =i F (w) , то

f (at ) =i

∞

8. Теорема свёртки. Если

(t ) = F (w) , то

(t ) f

(t ) =

−∞∫

(W) F

(w - W)dW .

Если

f (t ) = F (w) , то F (w) F (w)

∞

f (t) f

(t - t) d t .

i ∫

f (t ) =i

F (w) , то F (w ± W)

=i f

−∞

9. Теорема смещения. Если

(t )e

jΩt

∞

10. Теорема Рэлея. W = ∫ i (t )u (t ) dt = ∫ i2

(t ) Rdt , пусть i (t ) = f (t ),

R =1 Ом, тогда

∞

−∞

∞

−∞

∞

W = ∫ f 2 (t ) dt = ∫ f (t ) f

(t ) dt = ∫

f (t )×

∫ F (w)ejωt dwdt =

∫ F (w) ∫ f (t )ejωt dtdw ,

−∞

2p −∞

−∞

∞

−∞

∞

поскольку

∫ f (t )ejωt dt = F

(-w) , то W =

∫ F (w) F (-w) dw =

∫

| F (w) |2 dw =

∫ F 2

(w) dw .

−∞

Таким образом, получаем равенство вида:

∞	(t ) dt =	1	∞	F 2 (w) dw =	1	∞	(w) dw,
∫ f 2			∫			∫ F 2
		2p			p
−∞			−∞			0

где F 2 (w) – спектральная плотность энергии сигнала.

Некоторые выкладки по теме «Свойства преобразования Фурье»

∞

2. Взаимозаменяемость переменных t и ω F (-t ) = ∫ f (w)ejωt dw .

∞

−∞

∞

−∞

F (-w)

f (t ) =

∫ F (w)ejωt dw = ∫

e− jωt d (

-w) = ∫

e− jωt dw,

−∞

+∞

−∞

∞

F (w) = ∫

f (t )e− jωt dt,

F (-w) =

∫ f

(t )ejωt dt

−∞

Меняем местами t и ω

∞

f (w) = ∫

F (-t )

e− jωt dt,

f (w) =

∫ F (-t )e− jωt dt,

f (w)

−∞

2p −∞

∞

F (-t )

∫ f (w)ejωt dw, F (-t ) = 2p

∫ f (w)ejωt dw, F (-t )

−∞

i	1	F (-t )
=i
=i	2p
=i	2p f (w)
i

	i		d	i
4. Теорема о дифференцировании сигнала. Если	f (t ) =i	F (w) , то		f (t ) =i	jwF (w)
4. Теорема о дифференцировании сигнала. Если	f (t ) =i	F (w) , то	dt	f (t ) =i	jwF (w)
			dt

∞

jωt

∞

jωt

∞

jωt

(t ) =

∫ F

(w)e

dw = ∫ F (w)

dw = jw ∫ F (w)e

dw=i

jwF (w)

−∞

5. Теорема об интегрировании сигнала. Если f (t ) =i F (w) , то

f (t ) dt =i

∫

∞

−∞

∞

∫ f

(t ) dt = ∫

∫ F (w)ejωt dwdt =

∫ F

(w) ∫ ejωt dtdw =

∫ F (w)ejωt

−∞

∞

(w)e

jωτ

F (w)

∫ F

dw=i

−∞

f (t ) =i F (w) , то

6. Теорема запаздывания (смещения по времени). Если

1 F (w) . jw

τ dw =

−∞

f (t ± t ) =i F (w)e± jωt0

0 i

99 /102

∞

jω(t ±t0 )

∞

f (t ± t0 ) = ∫ F (ω)e

dω = e

± jωt0

∫ F

(ω)e

jωt

(ω)e

± jωt0

dω=i

−∞

7. Теорема сжатия. Если

(t ) =i

F (ω) , то

f (at ) =i

ω = aω

f (at ) = ∞

∞ F

ω ejωt d

ω =

∞

ω ejωt dω =i

F (ω )ejaω1t dω =

ω =

∫

a a

i a

−∞

8. Теорема свёртки. Если

(

) i

(

)

, то

(

)

= F

∞

∞ ∞

F1 (ω) F 2 (ω) = ∫ f1

(τ)e− jωτd τ ∫ f2

(θ)e− jωθdθ = ∫ ∫

−∞

−∞ −∞

F 2 (ω)		=i		∞	(τ) f2	(t − τ) d τ
F 2 (ω)		=i		∫ f1	(τ) f2	(t − τ) d τ
		i
				−∞			θ = t − τ
f	(τ) f	2	(θ)e− jω(τ+θ)d τdθ =				θ = t − τ	=
1		2
							dθ = dt

∞ ∞			− jω(τ+t −τ)	∞	∞				− jωt		∞
= ∫ ∫	f1 (τ) f	2 (t − τ)e	− jω(τ+t −τ)	dθdt = ∫	∫	f1 (τ) f	2 (t − τ) d τ	e	− jωt	i	∫ f1 (τ) f2 (t − τ) d τ
= ∫ ∫	f1 (τ) f	2 (t − τ)e		dθdt = ∫	∫	f1 (τ) f	2 (t − τ) d τ	e		dt =i	∫ f1 (τ) f2 (t − τ) d τ
−∞ −∞				−∞	−∞						−∞

Спектр функции Хевисайда.

∞

F (ω) = ∫ lim1(t )e−ct e− jωt dt = lim ∫

1(t )e− (c+ jω)t dt = lim ∫ e− (c+ jω)t dt = lim

e− (c+ jω)t

− (c + jω)

−∞ c→0

c→0 −∞

c→0 0

c→0

= lim

(

e− (c+ jω)∞ − e− (c+ jω)0

)

= lim

(0 −1)

= lim

e− j

− (c + jω)

c→0

c→0 c + jω

jω ω

∞ =

Спектры типовых сигналов

1. Спектр функции Хевисайда. Представим функцию Хевисайда в виде: 1(t ) = lim1(t ) e−ct .

c→0

∞

e− j

F (ω) = lim ∫ 1(t )e− (c+ jω)t dt = lim

– комплексная спектральная плотность.

c→0

−∞

c→0 c + jω

jω ω

– амплитудный спектр, φ(ω) = π –

F (ω) =

фазовый спектр.

2. Спектр δ -функции Дирака.

∞

F (w) = ∫ d(t )e− jωt dt = e0

= 1 , F (ω) = 1 –

амплитудный спектр,

φ(ω) = 0 – фазовый спектр.

−∞

∞

Так как ∫ d(t ) dt = 1, то F

(w) = ∫ d(t ) dt .

Взяв ОПФ

d(t ) =

∫ ejωt dw, и учитывая свойство

−∞

∞

−∞

и ω , получим: d(w)

взаимозаменяемости переменных t

= ∫ e± jωt dt .

3. Спектр постоянного сигнала f (t ) = E = const .

−∞

∞

F (w)

= ∫ Ee− jωt dt = E ∫ e− jωt dt = Ed(w) .

−∞

На частоте ω = 0 спектр F (0) = ∞ , на остальных частотах F (ω) = 0 .

4. Спектр гармонического сигнала f (t ) = E cos ω0t .

∞

jω0t

+ e

− jω0t

F (w) = ∫ E cos w0t ×e− jωt dt = E ∫

e− jωt dt =

−∞

	E	∞	∞		E	(d(w - w0 ) + d(w + w0 ))
=		∫ e− j(ω−ω0 )t dt + ∫ e− j(ω+ω0 )t dt		=

2		−∞	−∞	2

На частотах w = ±w0 спектр F (±ω0 ) = ∞ , на остальных частотах F (ω) = 0 . 5. Спектр прямоугольного импульса.

100

/102

tи

wtи

× 2

jwtи

- jwtи

E ×

sin

(w) = Etи

sin

F (w) = ∫ Ee- jwt dt = E

e 2

- e

2 =

, F

tи

2 j

wtи

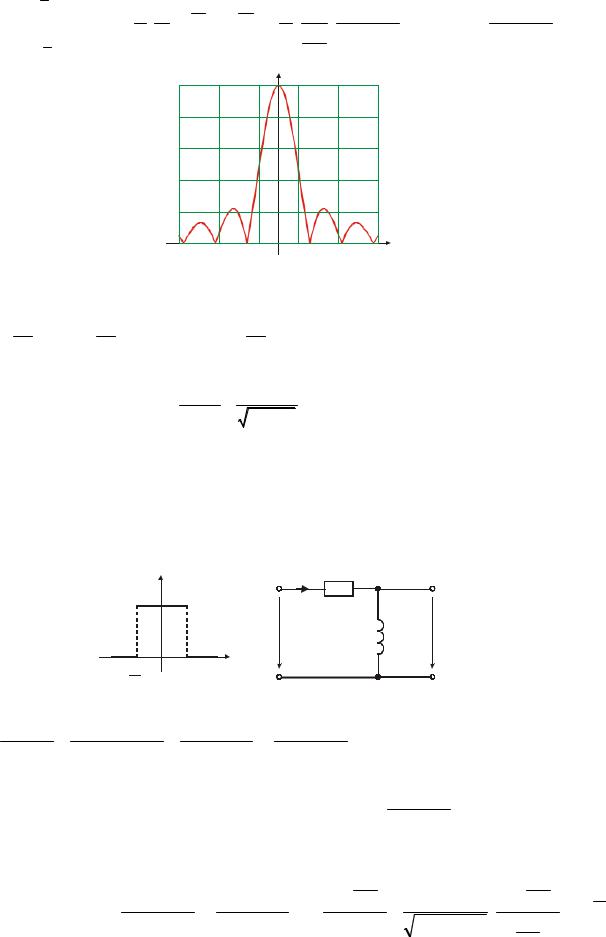
2,0

F(ω)

1,6

1,2

0,8

0,4

−10

−6

ω1

ω2

10 ω

Введём понятие ширины спектра сигнала

ω :

диапазон

частот,

относительно которого

сосредотачивается максимум энергии сигнала. Для прямоугольного импульса это

–

ширина

спектра по основному лепестку:

если w =

2π и w = - 2π , то Dw = w - w = 4π .

tи

6. Спектр экспоненциального импульса.

F (w) = ∫ e-at e- jwt dt = ∫ e-( jw+a)t dt =

- j×arctg

a .

-¥

jw + a

+ w

Частотный анализ ЛЭЦ при непериодических воздействиях

Для определения выходной реакции линейной электрической цепи используют комплексную

передаточную функцию H (w) . При этом спектр выходной реакции определяется в виде:

F 2 (w) = H (w) F 1 (w) .

U 2 (w)

Рассчитаем

комплексную

спектральную

плотность

выходного

сигнала

последовательной RL -цепи, если на её вход действует сигнал в форме прямоугольного импульса.

u1(t)

i(t) R

u1(t)

u (t)

− tи

tи

Комплексная передаточная функция определяется как:

H (w) =

jwL

jwL ( R - jwL)

(wL)2

+ j

wLR

R2 + (wL)2

R + jwL

R2 + (wL)2

wtи

Спектральная плотность прямоугольного импульса: U 1 (w) = Etи

sin

wtи

Комплексная спектральная плотность сигнала на выходе:

(

wtи

(w) = H (w)U

+ j

wLR

sin

j×arctg

(w) =

wL .

R2 + (wL)2

+ (wL)2

wtи

R2 + (wL)2

wtи

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.201958.88 Кб3ТЭИС темы,вопросы,литер..doc
#
10.11.2019210.94 Кб5ТЭИС. мет.КР.doc
#
22.08.201984.48 Кб4ТЭО-ПС-09.doc
#
10.06.20151.21 Mб42ТЭЦ контр.doc
#
11.11.2019313.34 Кб8ТЭЦ курсовая ВАРИАНТЫ 11-14 группы.doc
#
10.06.20152.64 Mб112ТЭЦ Лекции.pdf
#
10.06.20153.35 Mб179УИП Методическое пособие 2014.docx
#
29.03.2016548.84 Кб836УИП_краткий курс_2013.docx
#
27.11.2019682.5 Кб7УМК ОЭ от 12.04 11г..doc
#
27.11.2019430.59 Кб8УМК по ОСиП.doc
#
25.11.201918.81 Mб92УП КП 20.12.11.doc