
ТЭЦ Лекции
.pdf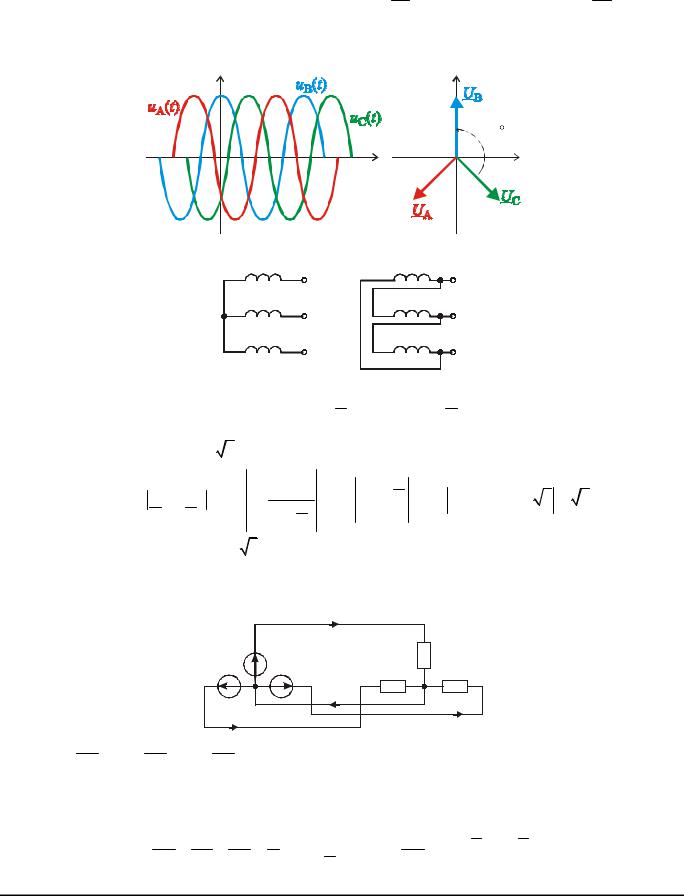
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
/102 |
В идеальном трансформаторе отношение, как токов, так и напряжений, не зависит от нагрузки, |
|
|||||||||||||||||
и определяются только коэффициентом трансформации kтр . |
|
|
|
|
|
|
|
|||||||||||
Анализ трехфазных электрических цепей. |
|
|
|
|
|
|
|
|
|
|
||||||||
Генератор трехфазной системы вырабатывает три гармонических напряжения равных |
|
|||||||||||||||||
амплитуд. Фазы этих напряжений сдвинуты относительно друг друга на угол 120º. |
|
|
|
|
||||||||||||||
uA (t ) = Um cos (ωt + ψ) , |
|
|
|
|
|
|
|
2p |
|
|
|
|
|
4p |
|
|||
uB (t ) = Um cos wt + y - |
3 |
, uC (t ) = Um cos wt + y - |
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
UA = UB = UC = Uф – фазные напряжения. Пусть y = π , тогда: |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
Re |
|
|
|
|
|
|
|
|
|
u(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
t |
|
|
0 |
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
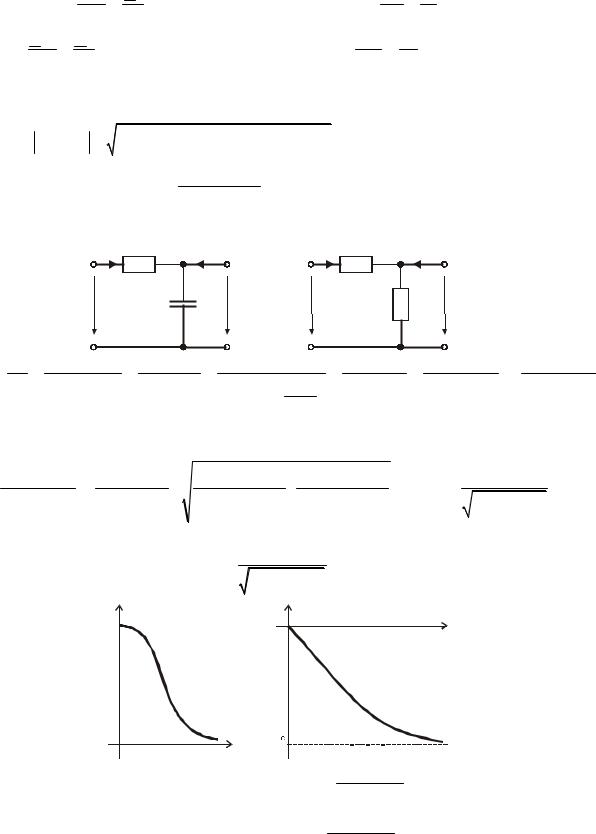
Три обмотки генератора могут соединяться между собой двумя способами: |
|
|
|
|
|
|||||||||||||
|
|
|
− |
uA(t) |
|
|
A |
− |
uA(t) |
+ A |
|
|
|
|
|
|
||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
||||||
|
|
|
− |
uB(t) |
|
|
B |
− |
uB(t) |
+ B |
|
|
|
|
|
|
||
|
|
0 |
|
+ |
|
|
|
|
|
|
|
|
||||||
|
|
− |
uC(t) |
|
|
|
− |
uC(t) |
+ C |
|
|
|
|
|
|
|||
|
|
|
|
|
C |
|
|
|
|
|
|
|||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
||||||
Напряжения на зажимах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U AB = U A -U B , U AС = U A -U С , U BС = U B -U C . |
|
|
|
|
|
|
||||||||||
|
|
UAB = UAC = UBC = U л – |
линейные напряжения. |
|
|
|
|
|
|
|||||||||
При соединении звездой: Uл = |
3Uф , действительно: |
|
|
|
|
|
|
|
|
|
||||||||
Uл = UAB = U A -U B = UA 1- |
e |
jϕ |
= Uф 1- e− j |
2π |
= Uф 1+ 0, 5 + j0, 5 |
3 = |
3Uф . |
|
||||||||||
|
2π |
3 |
|
|||||||||||||||
|
|
|
|
j ϕ− |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
e |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
Например: Uф = 127 В, тогда Uл |
= |
3 ×127 = 220 B . |
|
|
|
|
|
|
|
|
|
|||||||
При соединении треугольником: Uл = Uф . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Представим схему трехфазной цепи, у которой обмотки генератора и нагрузки соединены звездой. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
IA |
|
|
|
|
|
|
|
|
|
|
|
|
|
UA |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
UC |
|
|
UB |
|
Z |
С |
|
Z |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 |
|
|
|
IB |
|
|
|
|
|
|
|
|
|
IC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Токи I A = U A , I B |
= U B , |
I C = U C – |
линейные токи. |
|
|
|
|
|
|
|
|
|
||||||
ZA |
ZB |
ZC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С другой стороны: |
I 0 = I A + I B + I C , где I 0 |
– |
ток в нейтральном проводе. |
|
|
|
|
|
|
|||||||||
В режиме симметричной нагрузке ZA = ZB = ZC = Z , получаем: |
|
|
|
|
|
|
|
|||||||||||
I 0 = U A + U B + U C = 1 (U A |
+U B |
|
|
|
− j2π |
− j4π |
= 0 |
|
|
|
|
|||||||
+U C ) = U A 1+ e 3 + e |
3 |
|
|
|
|
|||||||||||||
|
Z |
Z |
Z |
Z |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
Ток в нейтральном проводе равен нулю, следовательно, его наличие в схеме необязательно. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42 |
/102 |
Комплексная |
|
передаточная |
|
функция |
|
|
(КПФ). |
|
Амплитудно-частотная |
|
|||||||||||||||
характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ). |
|
|
|
|
|
|
|
||||||||||||||||||
Комплексной передаточной функцией (КПФ) называется отношение комплексной |
|
||||||||||||||||||||||||
амплитуды (действующего значения) реакции цепи |
к комплексной амплитуде (действующего |
|
|||||||||||||||||||||||
значения) входного воздействия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
H U (ω) = U m 2 |
= U 2 – |
КПФ по напряжению; |
H I |
(ω) = I m2 |
= I 2 |
– КПФ по току; |
|
|
|||||||||||||||||
|
|
U m1 |
|
U 1 |
|
|
|
|
|
|
|
|
|
|
I m1 |
I1 |
|
|
|
|
|
|
|
||
H Z (ω) = U m 2 |
= U 2 – |
КПФ по сопротивлению; |
H Y |
(ω) = I m 2 |
= I 2 – КПФ по проводимости; |
|
|||||||||||||||||||
I m1 |
I 1 |
|
|
|
|
|
|
|
|
|
|
|
|
U m1 |
U 1 |
|
|
|
|
|
|
|
|||
В общем виде КПФ можно представить как: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
H X (ω) =H X (ω)ejj(w)=H X (ω)cos ϕ(ω) +j H X (ω)sin ϕ (ω) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где H X (ω) = H X (ω) = |
(Re (H X (ω)))2 + (Im (H X (ω)))2 |
|
– амплитудно-частотная характеристика |
|
|||||||||||||||||||||
|
|
|
|
|
|
Im (H X (ω)) |
– фазо-частотная характеристика (ФЧХ). |
|
|
||||||||||||||||
(АЧХ), ϕ(ω) = arg (H X (ω)) = arctg |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
Re (H X (ω)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
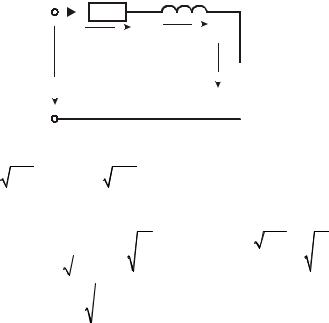
В качестве примера определим АЧХ и ФЧХ следующей цепи: |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
i1(t) R |
i2(t) |
|
|
|
I1 |
Z1 |
|
I2 |
|
|
|
|
|
|
|
||||||||
|
|
u (t) |
|
C u2(t) |
|
U |
1 |
|
|
|
Z2 U |
2 |
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
H U (ω) = U 2 = |
I1 |
I1 Z 2 |
|
= |
(Z1 |
Z 2 |
|
= |
|
1 |
1 |
|
= |
|
1 |
|
= |
1 |
|
− j |
ω R C |
|
|||
U 1 |
(Z1 + Z 2 ) |
|
+ Z 2 ) |
jωC |
|
|
1+ jω R C |
1+ |
(ω R C )2 |
|
1+ (ω R C )2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
R + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
jωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– КПФ по напряжению. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
КПФ можно представить в показательной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
ω R C |
|
|
1 |
|
|
(ω R C ) |
2 |
j×arctg -wR C |
|
|
1 |
|
- j×arctg(wR C ) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
H U (ω)=1+ (ω R C )2 − j1+ (ω R C )2 = |
(1+ (ω R C )2 )2 |
+ (1+ (ω R C )2 )2 e |
|
= |
|
1+ (ω R C )2 e |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из последнего выражения видно: H U (ω) = |
|
1 |
|
|
. АЧХ ϕ(ω) = −arctg (ω R C ) . ФЧХ. |
|
|||||||||||||||||||
1+ (ω R C )2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
H(ω) |
|
|
|
|
|
ϕ(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
ω |
−90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H X ( ω) |
|
|
|
|
|
|
|
|
||||
Для удобства анализа цепей вводят: H ( ω) = H Xnorm ( ω) = |
|
– нормированная КПФ; |
|
||||||||||||||||||||||
H X (ω)max |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
H (ω) = H Xnorm |
(ω) = |
|
H X (ω) |
– |
нормированная АЧХ, |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
H X (ω)max |
|
|
|
|
|
|
|
|
||||
Введем понятие: |
D (ω) = ln H (ω) |
[Нп]; D (ω) = 20 lg H (ω) [дБ] – |
усиление. |
|
|
|
|
||||||||||||||||||
43 /102
|
1 |
1 |
|
|
A(ω) = ln |
|
[Нп]; A(ω) = 20 lg |
|
[дБ] – ослабление. |
H (ω) |
H (ω) |
|||
[Нп] – непер, [дБ] – децибел, причем 1 дБ ≈ 0,115 Нп, 1 Нп ≈ 8, 69 дБ . Для оценки частотных интервалов вводят понятия: октава и декада.
Октава – внесистемная безразмерная относительная единица интервала (логарифмический интервал) между двумя значениями, отношение которых равно 2.
Декада – внесистемная безразмерная относительная единица интервала (логарифмический интервал) между двумя значениями, отношение которых равно 10.
В интервале частот [ω1 , ω2 ] |
число октав и декад рассчитываются соответственно: |
||||||
Nоктав = log |
ω2 |
ω2 |
, то есть 1 октава = 0,301 декады, 1 |
декада = 3,32 |
|
||
2 ω |
, Nдекад = lg ω |
|
октавы . |
||||
|
1 |
1 |
|
|
|
|
|
Например: |
ω2 |
= 4 , Nоктав = 2 |
, если |
ω2 = 100 , Nдекад = 2 . |
|
|
|
|
ω1 |
|
|
|
ω1 |
|
|
Последовательный колебательный контур. Основные понятия и определения.
|
|
|
|
i(t) |
|
R |
|
L |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
uL(t |
) |
|
||||||
|
|
|
|
|
|
|
uR(t) |
C |
||||||||||||
|
|
|
|
|
|
u(t) |
|
uC(t) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеет место резонанс напряжений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Резонансная частота: ω0 = |
|
1 |
|
, f |
0 = |
1 |
|
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
L C |
|
2 π L C |
|
|
|
|
|
|
|
|
|
|||||||
Резистивное сопротивление контура при резонансе. Z = R .
Определим реактивные сопротивления на индуктивности и емкости при резонансе:
|
|
X |
= ω L = |
|
1 |
|
|
|
L = |
|
L |
, X |
= |
1 |
= |
|
LС |
= |
L |
. |
||||||||
|
|
|
|
|
|
|
|
|
ω0C |
|
|
|
|
|||||||||||||||
|
|
|
L0 |
|
0 |
|
|
|
L C |
|
|
|
|
|
|
C |
C0 |
|
С |
C |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Видно, что сопротивления X |
|
= X |
|
|
= |
|
|
L |
|
= ρ – характеристическое сопротивление контура. |
||||||||||||||||||
L0 |
C0 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Резонансные свойства контура характеризуются добротностью: |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Q = 2 π |
Wp |
, |
|
|
|
|
|
|
|
(76) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wa T |
|
|
|
|
|
|
|
|
|
|||
где Wp |
– максимальное значение реактивной энергии, запасенной в контуре при резонансе; |
|||||||||||||||||||||||||||
W |
– |
активная энергия, поглощаемая в контуре за период T; |
d = |
1 |
– затухание. |
|||||||||||||||||||||||
|
||||||||||||||||||||||||||||
a T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для выяснения физического смысла параметра Q исследуем энергетические соотношения в контуре при резонансе. Обозначим резонансный ток как i = Im 0
В контуре происходит периодический обмен энергии электрического и магнитного полей, то есть
W = |
L Im2 |
0 |
= |
C Um2 |
0 |
= const . |
(77) |
|
|
|
|
||||
p |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
Значение активной энергии, рассеиваемой в контуре, определяется как:
W |
= I 2 |
R T = |
Im2 |
0 R T |
. |
(78) |
|
|
|||||
a T |
0 |
|
|
2 |
|
|
|
|
|
|
|
|
С учетом (76 – 78) получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44 |
/102 |
|
|
L Im2 |
|
2 π f |
0 |
|
L ω L ρ |
|
|
|
|
|
|
|
ω L ω2 L 1 |
|
L |
1 |
ρ |
|
||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
= R |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
= R ω L C |
= R ω C = |
R . |
|
|||||||
Q = 2 π I 2 R T = |
R |
|
|
|
|
= |
|
|
R |
|
|
, либо Q = |
R |
|
= |
R |
|
ω |
|
|||||||||||||||||||||||
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = |
L |
= |
|
1 |
|
= |
. |
|
|
|
|
|
|
|
|
|
(79) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R ω0 C |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, добротность Q показывает, во сколько раз резонансные напряжения на |
|
|
||||||||||||||||||||||||||||||||||||||||
реактивных элементах превышают приложенное напряжение. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Величины R, L, C являются первичными параметрами контура. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Величины ρ, ω0 , Q, d являются вторичными параметрами контура. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Частотные характеристики последовательного колебательного контура. |
|
|
||||||||||||||||||||||||||||||||||||||||
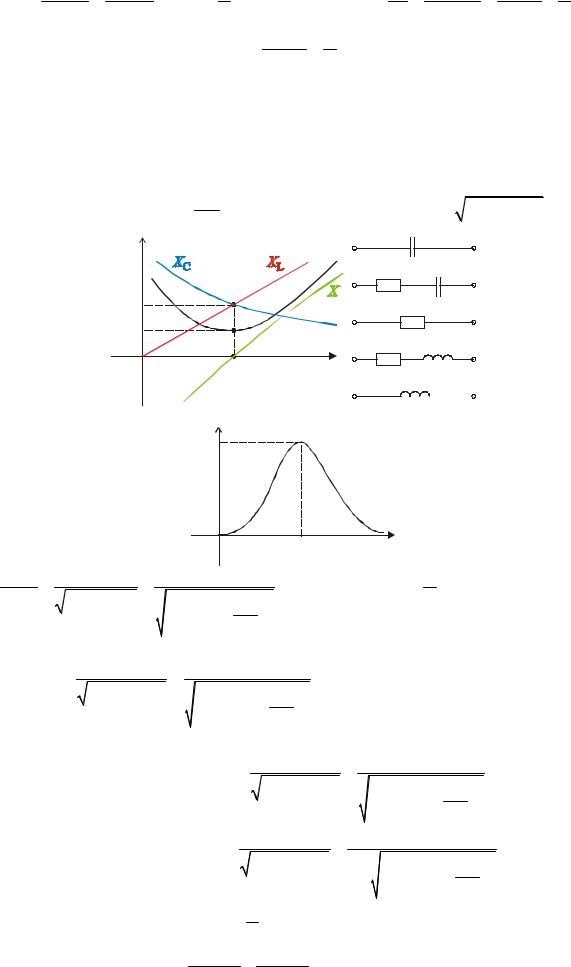
Из-за наличия в контуре реактивных элементов, видно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
X L (ω) = ω L , X C (ω) |
= |
|
1 , X (ω) = X L (ω) − X C (ω) , Z (ω) = R2 + X 2 (ω) , |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
X, Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω → 0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
0 < ω < ω0 |
|
|
|
|||
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = ω0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 < ω < ∞ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω → ∞ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определим частотную зависимость тока (резонансную характеристику тока) в контуре: |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|||
I(ω) = |
U |
= |
|
U |
|
|
|
= |
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
, при резонансе: I0 |
= U |
– |
максимальное значение. |
|
||||||||||||||
|
Z (ω) |
R2 +X 2 (ω) |
|
|
|
|
|
2 |
|
ωL− |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
+ |
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Определим частотные зависимости напряжений на отдельных элементах контура: |
|
|
||||||||||||||||||||||||||||||||||||||||
UR (ω) = I (ω) R = |
|
U R |
|
|
(ω) |
|
= |
|
|
|
|
|
|
|
|
U R |
|
|
|
, при резонансе: UR (ω0 ) = I0 R = U . |
|
|
||||||||||||||||||||
R2 + X 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
R |
2 |
+ |
ωL − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
резонансные характеристики напряжений: |
|
|
U X L ( |
ω) |
|
|
|
|
|
|
|
U ωL |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
UL (ω) = I (ω) X L (ω) = |
|
|
|
|
= |
|
|
|
|
|
|
, |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
R2 + X 2 (ω) |
|
|
|
|
|
|
1 2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
2 |
+ |
ωL − |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U X C (ω) |
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|||||
|
|
|
|
UC (ω) = I (ω) X C (ω) = |
|
|
|
= |
|
|
|
|
|
|
U |
|
|
, |
|
|
||||||||||||||||||||||
|
|
|
|
|
R2 + X 2 (ω) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
R |
2 |
|
|
1 |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ωL − |
ωC |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ = U ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
при резонансе: U |
L |
(ω ) = U |
C |
( |
ω |
|
) |
= I |
0 |
|
= U Q , откуда определим добротность: |
|
|
|||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UL (ω0 ) |
= |
UC (ω0 ) |
= Q . |
|
|
|
|
|
|
|
|
|
|
(80) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
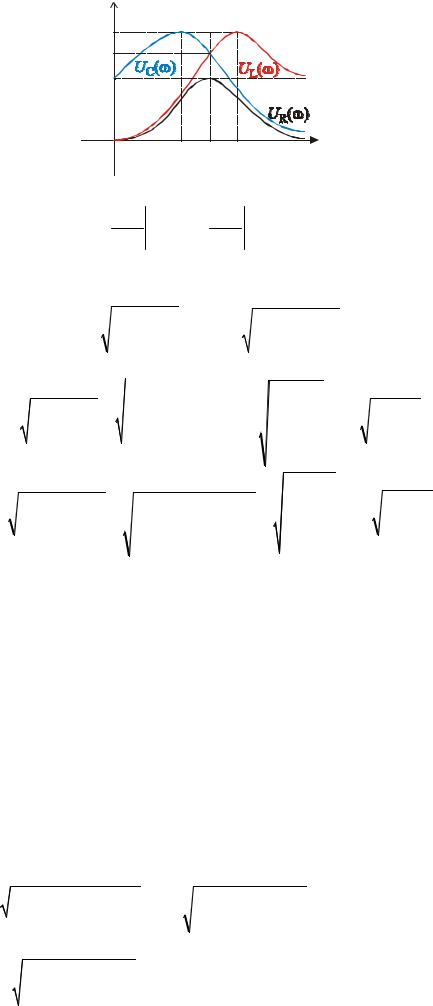
45 /102
|
|
U(ω) |
|
|
|
|
|
|
|
Umax |
|
|
|
|
|
|
|
Uр |
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
0 |
|
ωC |
ω0 ωL |
ω |
|
|
Максимальные значения достигаются на частотах ωC и ωL : UC (ωC ) = UC max , UL (ωL ) = UL max . |
||||||
ωC |
|
d UC |
= 0 , |
d UL |
|
= 0 . |
|
и ωL определяются из условий: |
d ω |
d ω |
|
||||
|
|
|
ω=ωC |
ω=ωL |
|
||
Получаем уравнения: |
2 L2 C ωC2 |
+ R2 C − 2 L = 0 , |
2 + ωL2 (R2 C2 − 2 L C ) = 0 . |
||||
Полученные уравнения вывести самостоятельно |
|
|
|
||||
|
|
|
ω = |
|
|
|
2 L − R2 C |
|
, ω = |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 L C − R2 |
C2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
C |
|
|
|
|
|
|
2 L2 C |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Определим частоты максимумов через добротность и резонансную частоту контура: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 L − R |
2 |
|
|
|
|
|
|
R |
|
C |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
−1 |
|
|
|
|
|||||||||||||||
|
|
|
C |
|
|
|
|
C R |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 Q |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ω = |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= ω |
|
. |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
C |
|
2 L2 C |
|
|
|
|
|
|
|
|
|
|
2 L2 C |
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ2 |
|
|
1 |
|
|
|
|
0 |
|
2 Q2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 ω02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
ω |
|
|
|
|
|
|
2 Q |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
ωL = |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
0 |
|
|
= ω0 |
|
|
|
|
|
|
. |
|||||||||||||||||||||
2 L C − R2 C 2 |
|
|
|
|
2 |
|
2 |
|
L 1 |
|
− |
|
|
|
|
|
|
ρ2 |
|
|
|
|
|
|
|
2 Q2 −1 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
C |
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C R |
|
R |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Комплесные передаточные функции по напряжению относительно элементов C, L и R:
|
|
U C(ω) |
|
|
|
I |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1− ω2 LC |
|
|
|
|
|
|
|
|
|
ωCR |
|
|
|||||||||||||||
H U (ω)= |
= |
|
|
|
jωC |
|
|
= |
|
|
1 |
|
|
|
= |
|
|
|
|
|
|
|
−j |
|
|
|
|
|||||||||||||||||||||||
U |
(ω) |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
2 |
||||||||||||
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1−ω |
LC+jωCR |
|
1− ω LC |
|
|
+ |
ωCR |
|
|
|
|
|
|
1− ω LC |
|
|
|
+ ωCR |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
I R+j ωL− |
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
( |
|
|
|
) |
|
|
|
|
( |
|
|
) |
|
|
( |
) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
U L (ω) |
|
|
|
|
jωLI |
|
|
|
|
|
|
|
ω2 L2 − |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
ωLR |
|
|
|
|
|
|
|
|
||||||
|
H U |
(ω) = |
= |
|
|
|
|
|
|
= |
|
|
|
C |
|
|
|
|
+ j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
U (ω) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I R + j |
ωL − |
|
|
|
R |
|
+ |
ωL − |
|
|
|
|
|
|
|
|
R |
|
|
+ |
ωL − |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|||||||||
|
|
|
H U |
|
(ω) = |
|
U |
R (ω) |
= |
|
|
|
|
|
|
I R |
|
|
|
|
|
= |
|
|
|
|
R2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
R |
|
|
|
U |
(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
1 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I R + j |
ωL − |
|
|
|
R |
|
+ |
ωL − |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
ωC |
||||||||
АЧХ последовательного контура: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
H UC (ω) = |
|
H UC (ω) |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
( |
|
|
|
|
2 |
|
|
) |
2 |
( |
ωCR |
) |
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−ω LC |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
R + ωL − |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
||||
H UL (ω) = |
|
H UL |
(ω) |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
+ |
ωL − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ωL − |
|
1 |
|
||
|
|
R |
|
|
|
||||
|
|
|
|
||||||
− j |
|
|
|
|
|
ωC |
|||
|
2 |
+ |
|
ωL − |
1 |
|
2 |
||
|
|
|
|||||||
|
R |
|
|
|
|
|
|||
|
|
|
|||||||
|
|
|
|
|
|
|
ωC |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
/102 |
|
H UR (ω) = H UR (ω) = |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
R |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
+ ωL − |
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
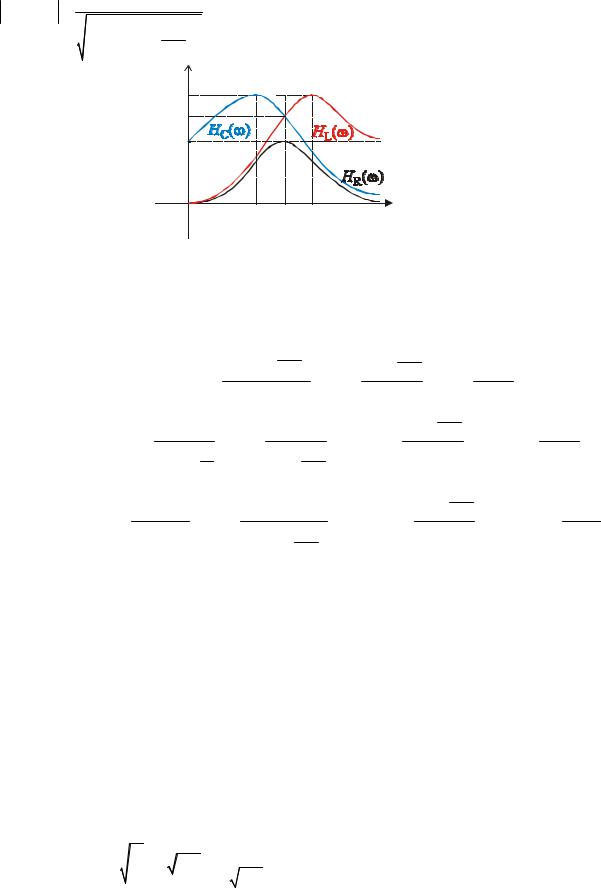
|H(ω)| |
|
|
HCmax |
|
HLmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
ωC |
ω0 |
|
ωL |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При ω = ω0 : HL (ω0 ) = HC (ω0 ) = Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Максимальные значения также достигаются на частотах ωC и ωL : HC (ωC ) = HC max , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
HL (ωL ) = HL max . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Самостоятельно построить частотные характеристики фазовых соотношений. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ωL − |
1 |
|
|
|
|
ωL − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
X |
( |
ω |
) |
|
|
|
|
|
|
|
|
|||
|
ϕU |
(ω) = arg (H R (ω)) = arctg |
|
|
ωC |
= arctg |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
R2 |
ωC = arctg |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
|
||
|
ϕUL (ω) = arg (H L (ω)) = arctg |
|
ωLR |
|
|
|
|
|
|
|
= π |
|
ωL − |
1 |
|
|
X |
( |
ω |
) |
|
|
|
|||||||
|
|
= arctg |
|
|
|
|
− arctg |
|
|
|
|
|
|
|||||||||||||||||
|
|
R |
1 |
ωC = π − arctg |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
2 |
|
R |
2 |
|
|
R |
|
|
|
|
|
|
||||
|
|
|
|
|
|
ω2 L2 − C |
|
|
ωL − |
ωC |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL − 1 |
|
|
|
|
|
X |
( |
ω |
) |
|
||
ϕU |
(ω) = arg (H C (ω)) = arctg |
−ωCR |
= arctg |
−R |
|
|
|
= − π − arctg |
ωC = − π − arctg |
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
C |
|
|
|
1− ω2 LC |
|
|
|
|
|
|
|
2 |
|
R |
|
2 |
|
|
|
|
R |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
− ωL − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Передаточная функция по проводимости последовательного колебательного |
|
|||||||||||||||||||||||||||||
контура. Абсолютная, относительная и обобщённая расстройка, полоса |
|
|||||||||||||||||||||||||||||
пропускания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комплексная передаточная функция по проводимости контура: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω L − |
1 |
|
|
|
|
||
H Y (ω) = |
I |
= |
1 |
= |
|
1 |
|
|
= |
|
R |
|
|
− j |
ωC |
|
. |
(81) |
||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|||||||
U Z (ω) |
|
|
|
|
1 |
|
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
R + j |
ω L − |
|
|
|
R2 + |
ω L − |
|
|
R2 + |
ω L − |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
ωC |
|
|
|
ωC |
|
|
|
|
ωC |
|
|
||||
Степень отклонения режима колебательного контура от резонанса оценивают по:
Δω = ω − ω0 или |
|
f |
= f − f0 – абсолютной расстройке, |
||
δ = |
Δω |
= |
f |
f |
– относительной расстройке, |
|
ω |
|
0 |
|
|
|
0 |
|
|
|
|
|
X (ω) |
|
ω L − |
1 |
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
ω |
|
ω |
|
|
|
|
|
ωC |
|
1 L |
|
|
1 |
|
|
|
|||||||||||||
ξ = |
= |
R |
= |
L C − |
= |
− |
= Q ν – обобщённой расстройке. |
||||||||||||||||
R |
|
R C |
ω |
ω L C |
|
R |
|
ω |
ω |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В теории часто применяется обобщённая расстройка, так как её использование упрощает расчёт, то есть
H Y (ξ) = |
|
1 |
= HY (ξ)ejϕY (ξ) |
, |
(82) |
|
R (1 |
+ jξ) |
|||||
|
|
|
|
47 /102
где HY (ξ) = |
|
1 |
|
: АЧХ, ϕY (ξ) = −arctg ξ : ФЧХ. (Построить самостоятельно!) |
|
|
|
|
|
||
|
R |
1+ ξ2 |
|||
Мы можем более упростить расчёт, если будем использовать нормированную АЧХ:
H(Y (ξ) ) =
HY ξ = 0
1 |
HY(x) |
|
|
|
1 |
|
|
|
|
Ö 2 |
|
|
|
|
x1 |
0 |
x2 |
x2 |
x¢ |
Полоса пропускания (ПП) – диапазон частот в пределах которого коэффициент передачи уменьшается в 2 раз. Определим граничные частоты полосы пропускания из условия:
|
|
|
|
|
|
H |
|
|
|
|
(ξ) = |
1 |
|
= |
|
|
|
1 |
, откуда ξ = −1, ξ |
|
= 1. |
|||||||
|
|
|
|
|
|
Ynorm |
|
|
|
|
|
|
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
+ ξ2 |
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ω |
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С другой стороны: ξ = Q |
|
− |
ω |
, тогда истинные частоты: |
|
|
||||||||||||||||||||||
ω |
|
|
||||||||||||||||||||||||||
|
ω0 |
|
|
|
|
|
0 |
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ω = |
|
|
−1 |
, ω = |
|
|
|
+1 . |
|
|
|
|
|
|
|
|||||||||||||
1+ 4 Q2 |
1+ 4 Q2 |
|
|
|
|
|
|
|
||||||||||||||||||||
2 Q |
2 Q |
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим ширину полосы пропускания: |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
Π |
ω |
= ω − ω = ω0 |
, либо Π |
|
= |
f0 |
. |
|
(83) |
|||||||||||
|
|
|
|
|
|
|
|
f |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
Q |
|
|
|
Q |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Избирательность – способность контура выделять колебание определённой частоты. Выводы:
1.С увеличением потерь в контуре, его добротность уменьшается.
2.Уменьшение добротности способствует увеличению полосы пропускания.
3.Увеличение полосы пропускания ведёт к уменьшению избирательности.
Параллельный колебательный контур. Основные понятия и определения.
Частотные характеристики параллельного колебательного контура.
Принцип дуальности позволяет распространить частотные характеристики последовательного колебательного контура на частотные характеристики параллельного контура. В параллельном колебательном контуре имеет место резонанс токов с частотой:
|
|
|
|
|
|
|
|
|
|
i(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iL(t) |
|
iC(t) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
u(t) |
|
iG(t) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
При резонансе: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
Y = G , ω = |
|
, f |
|
= |
. B = ω C = |
|
|
|
C = |
|
C |
|
= g , |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
|
LC |
|
0 |
|
2π LC |
C0 |
0 |
|
|
|
|
L C |
|
|
|
|
L |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где g – характеристическая проводимость контура. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Добротность определяется как: |
|
|
ω0 C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Q = |
= |
|
1 |
|
|
= |
g |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
G ω0 L |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
G |
|
|
|
|
|
||||||||
B = |
1 |
|
= |
L С |
= |
C |
= g , |
ω0 |
|
|
|
||||
L0 |
L |
L |
L |
||||
|
|||||||
(84)
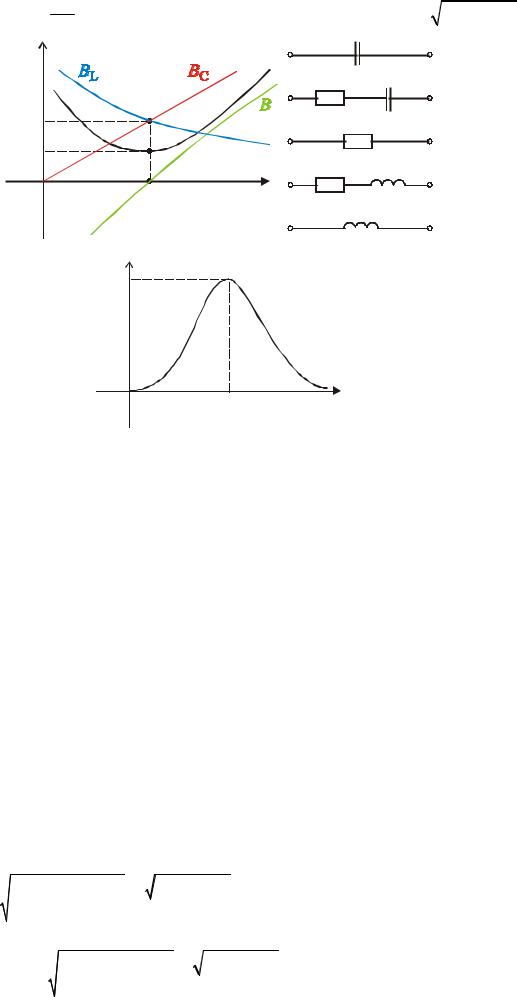
48 /102
BC (ω) = ωC , BL (ω) = |
1 , B (ω) = BC (ω) − BL (ω) , Y (ω) = G + jB (ω) , Y (ω) = G2 + B2 (ω) , |
|
|
ω L |
|
B, Y |
|
ω → ∞ |
|
Y |
ω0 < ω < ∞ |
g |
|
ω = ω0 |
|
|
|
G |
|
0 < ω < ω0 |
|
ω0 |
|
0 |
ω |
|
|
|
ω → 0 |
Определим частотную зависимость напряжения в контуре: |
||
|
U(ω) |
|
|
U0 |
|
0 |
ω0 |
ω |
Если к цепи подключен источник тока i (t ) = I , то напряжение на элементах контура определяется
|
|
|
|
|
|
|
U (ω) |
= |
|
I |
|
|
= |
|
|
I |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Y (ω) |
G + jB (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
При резонансе токов: ϕ = arctg |
B |
= 0 , то есть B ( |
ω) = B |
|
(ω) − B |
(ω) = 0 , тогда U |
|
= |
I |
. |
|||||||||||||||||||||||
|
|
0 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
C |
|
|
|
L |
|
|
|
|
|
|
|
G |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Определим частотные зависимости токов на отдельных элементах контура: |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC − |
|
1 |
|||
|
|
|
I G |
|
|
I G |
|
|
|
|
|
|
|
|
|
I G |
2 |
|
|
|
|
|
I G |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
I G (ω) = |
|
(ω)G = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|||||||||
U |
|
= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
− j |
|
|
|
|
|
|
|
|
||||||
G + jB (ω) |
|
|
|
1 |
|
|
|
2 |
|
|
|
|
1 |
|
2 |
|
2 |
|
|
|
1 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
G + j ωC − |
|
|
|
|
G |
|
+ |
ωC − |
|
|
|
|
G |
|
+ |
ωC − |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
ωL |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
I BC (ω) |
|
|
|
|
|
|
|
|
|
I ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
I ωCG |
|
|
|
|
IωC |
ωC − |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
I C (ω) = U (ω) BC (ω) = |
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
− j |
|
|
|
|
|
|
|
ωL |
|
||||||||||||||||||||||||||||||||||||||
G + jB (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
|
|
1 2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G + j |
ωC − |
ωL |
|
|
|
|
G |
|
+ |
|
ωC − |
|
|
G |
|
+ ωC − |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
ωL |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
ωC − |
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
I BL (ω) |
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
G |
|
|
|
|
I |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
I L (ω) = U (ω) BL (ω) = |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
ωL |
|
|
− j |
|
|
ωL |
|
|
|
ωL |
|
|||||||||||||||||||||||||||||||||||
G + jB (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
2 |
|
|
2 |
|
|
|
|
1 2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G + j |
ωC − |
|
ωL |
|
|
|
|
G |
|
+ |
ωC − |
|
|
|
G |
|
+ ωC − |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
ωL |
|||||||||||||||||||
Частотные зависимости амплитуды токов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
IG (ω) = |
|
I G (ω) |
|
= |
|
|
|
|
|
I G |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
I G |
|
|
|
|
|
|
|
, |
при резонансе: IG (ω0 ) = I . |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
1 |
|
2 |
G2 + B2 (ω) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
G |
|
|
+ ωC |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I BC (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
IC (ω) = |
|
I C (ω) |
|
= |
|
|
|
|
I ωC |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
, при резонансе: IC (ω0 ) = |
Iω C |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ B2 (ω) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
G2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
+ ωC |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

49 /102
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I BL (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
IL (ω) = |
|
I L (ω) |
|
= |
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
, при резонансе: IL (ω0 ) = |
|
|
I |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G2 + B2 (ω) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
+ |
|
ωC − |
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gω0 L |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
При резонансе: |
|
|
I |
|
|
(ω ) |
= I |
|
(ω ) = U |
|
|
|
g = I |
g |
|
= I Q , откуда определим добротность: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
C |
L |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IC ( |
ω0 ) |
|
|
|
(ω0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
IL |
|
= Q . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(85) |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Комплексные передаточные функции по току: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
I G (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
H I |
|
(ω) = |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
G |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
G + j |
ωC |
− |
|
ωL |
|
|
|
|
|
|
|
|
|
G |
|
|
|
+ |
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
+ ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
I C (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
jωCI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωCG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
H I |
|
(ω) = |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
C |
|
|
I |
|
|
|
|
|
+ j |
|
ωC − |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
G |
|
ωL |
|
|
|
|
|
|
|
G |
|
|
|
|
+ |
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
+ ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
I L( |
ω) |
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
H |
|
(ω) = |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
IL |
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I G + j |
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
+ ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
+ ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Частотные зависимости фазовых соотношений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−G |
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
( |
ω |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
ϕI (ω) = arg (H I |
|
|
|
(ω)) = arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
= −arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
= −arctg |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
G |
|
|
|
|
|
|
|
G2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ϕIC (ω) = arg (H IC |
|
(ω)) = arctg |
|
|
|
|
|
|
|
ωCG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= π − arctg |
ωC − |
|
|
1 |
|
|
= π |
|
|
|
|
|
( |
ω |
) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= arctg |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
ωL |
− arctg |
B |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
G |
|
|
|
G |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC − |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
ωC − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ϕIL (ω) = arg (H IL |
|
(ω)) = arctg |
|
|
|
|
|
|
|
|
− |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − π − arctg |
|
ωC − |
1 |
|
= − π − arctg |
|
|
( |
ω |
) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
B |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
G |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
ωC |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Передаточная функция по сопротивлению параллельного колебательного контура.
Метод узкополосного приближения
Комплексная передаточная функция по сопротивлению параллельного контура:
|
H Z (ω) = |
|
U |
|
= |
1 |
|
|
= |
|
|
|
|
1 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
Y (ω) |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G + j |
ωC − |
|
|
|
|
|
|
G |
|
|
+ |
ωC − |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|||||||
|
B (ω) |
|
ωC − |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g ω |
|
|
ω |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
ω L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
1 C |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
ξ = |
= |
|
|
|
|
|
|
|
= |
|
ω L C − |
|
|
|
|
|
|
= |
− |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||||
|
G |
|
|
|
G |
|
|
|
|
G L |
|
|
|
|
|
|
|
|
ω |
L C |
|
|
|
G |
ω |
|
|
ω |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H Z ( |
ξ) |
= |
|
|
|
1 |
|
|
|
= HZ (ξ)ejϕZ (ξ) , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G (1 |
+ jξ) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
ωC − |
1 |
|
|
|
|
||
− j |
|
|
ωL |
|
. |
(86) |
||||
|
|
|
|
|
||||||
|
2 |
|
|
|
1 |
2 |
||||
|
G |
|
+ |
ωC − |
|
|
|
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
ωL |
|
|||
= Q ν – обобщённая расстройка.
(87)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
/102 |
где H Z (ξ) = |
|
1 |
|
: АЧХ, ϕZ (ξ) = −arctg ξ : ФЧХ. (Построить самостоятельно!) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
G 1 |
+ ξ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H Znorm |
(ξ) = |
H Z (ξ) |
|
|
= |
|
|
|
1 |
|
|
|
– |
коэффициент передачи по сопротивлению. |
|
|
|
||||||||||||||||||||||||||||||||
H Z (ξ = 0) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
1 |
+ ξ2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Определим граничные частоты полосы пропускания из условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
H |
|
|
|
|
(ξ) = |
|
|
1 |
= |
|
1 |
|
, откуда ξ = −1, |
ξ |
|
= 1. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
Znorm |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1+ ξ2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ω |
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1+ 4 Q |
2 |
−1) |
|
|
( |
|
|
2 |
+1) . |
|
|||||||||||||||
Так как ξ = Q |
|
− ω |
, то истинные частоты: ω1 = |
|
|
|
, ω2 = |
|
1+ 4 Q |
|
|
||||||||||||||||||||||||||||||||||||||
ω |
2 Q |
|
2Q |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим ширину полосы пропускания: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Π |
ω |
= ω − ω = ω0 , либо Π |
|
|
= |
f0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(88) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
Q |
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приближенный переход от ω к переменной |
|
|
ω = ω − ω0 |
|
составляет |
сущность метода |
|
||||||||||||||||||||||||||||||||||||||||||
узкополосного приближения (Δω ω0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ω ω0 |
|
|
Δω + ω0 |
|
|
ω0 |
|
|
|
|
|
Δω |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
ν = |
|
|
− |
ω |
= |
|
|
ω0 |
|
|
− |
|
= 1+ ω0 |
− |
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
ω0 |
|
|
|
|
Δω + ω0 |
|
|
|
Δω |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
ω |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Последнее слагаемое разлагаем в ряд: |
|
|
|
|
|
1 |
|
|
= 1 x + x2 x3 + x4 ..., |
x2 < 1. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
1± x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(Г. Б. Двайт. Таблицы интегралов и другие математические формулы. М. :Наука. 1983. стр. 6 ф. 9.04)
|
1 |
|
|
Δω −1 |
Δω |
|
Δω 2 |
ω |
|
ω |
|
2Δω |
|||
|
|
= 1 |
+ |
|
= 1− |
|
+ |
|
−…, то ν = |
|
− |
0 |
≈ |
|
. |
|
Δω |
ω0 |
ω0 |
ω |
|
||||||||||
1+ |
|
|
ω0 |
|
|
ω0 |
|
|
|
ω0 |
|||||
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частотные характеристики имеют упрощённый вид:
H Znorm (ω) = |
1 |
|
≈ |
|
|
|
1 |
|
|
|
|
, ϕZ (ω) = −arctg ν Q ≈ −arctg Q |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1+ (νQ)2 |
|
|
|
|
|
|
|||||||
|
|
|
1+ Q |
2 |
|
2Δω |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ω |
||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
||
Параллельный колебательный контур с потерями
(89)
2 Δω . ω0
i(t)
R1 R2
u(t)
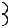 L C
L C
Определим эквивалентное комплексное сопротивление цепи:
|
|
|
|
|
|
|
|
Z э |
= |
( R1 + j X L )( R2 |
|
− j X C ) |
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
R1 |
+ R2 |
+ j( X L |
− X C ) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пусть R1 X L , R2 X C (малые потери), тогда |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Z э |
= |
|
|
|
X L X C |
|
|
, так как X L X C = |
|
L |
, то |
|
|
||||||||||
|
|
|
|
|
R1 |
+ R2 + j( X L − X C ) |
|
C |
G′ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Z э = |
|
|
1 |
|
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
= |
|
1 |
|
= |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
G′ |
|
|
|
|
+ B2 |
||||||
|
C |
R + R + j |
ω L − |
1 |
|
|
C |
(R + R ) + j |
ωC − |
|
+ j B G′2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 2 |
|
|
|
|
|
|
L |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
|
|
|
|
ωC |
|
|
|
|
|
|
|
ω L |
|
|
|
|
|
|
|
|
||||||
(90)
− j B .
G′2 + B2
