Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТЭЦ Лекции

.pdf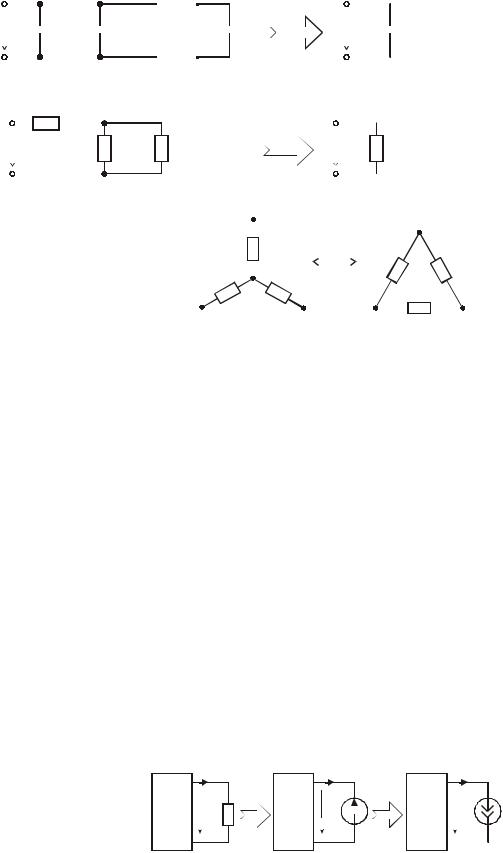

Скачиваний:

112

Добавлен:

10.06.2015

Размер:

2.64 Mб

Скачать

☆

<<< < Предыдущая 12 / 112 3 4 5 6 7 8 9 10 11 > Следующая >>>

11 /102

Cэкв

Cэкв = ∑Cn .

(26)

n=1

4. Смешанное соединение резистивных элементов:

Rэкв

= R +

R2 R3

(27)

экв

R2 + R3

Преобразование из «звезды» в «треугольник» и обратно

r12

r31

r23

Для сопротивлений из «звезды» в «треугольник» r

= r + r

r1r2

; r

= r

+ r

r2 r3

; r

= r

+ r +

r3r1

Для проводимостей из «звезды» в «треугольник»

g12

g1 g2

; g23 =

g2 g3

; g31

g3 g1

+ g2

g1 + g2 + g3

+ g2 + g3

+ g3

Для сопротивлений из «треугольника» в «звезду»

r1 =

r12 r31

; r2 =

r23r12

; r3

r31r23

r12 + r23 + r31

r12

+ r23 + r31

r12

+ r23

+ r31

Для проводимостей из «треугольника» в «звезду»

g = g + g

g12 g31

; g

= g + g

g12 g23

; g

= g

+ g

g23 g31

g23

g31

g12

Принцип наложения. Теорема замещения. Теорема взаимности.

На этом принципе основан метод суперпозиции (наложения) анализа электрических цепей.

Напряжения и токи источников электрической

энергии

– воздействия,

а напряжения и токи

в отдельных ветвях цепи –

реакции.

Принцип

наложения

можно

сформулировать

следующим

образом: реакция

линейной

электрической цепи (ЛЭЦ) на сумму воздействий равна сумме реакций от каждого воздействия в отдельности.

	N					N
	i = ∑in ,				u = ∑un .			(28)
	n=1					n=1
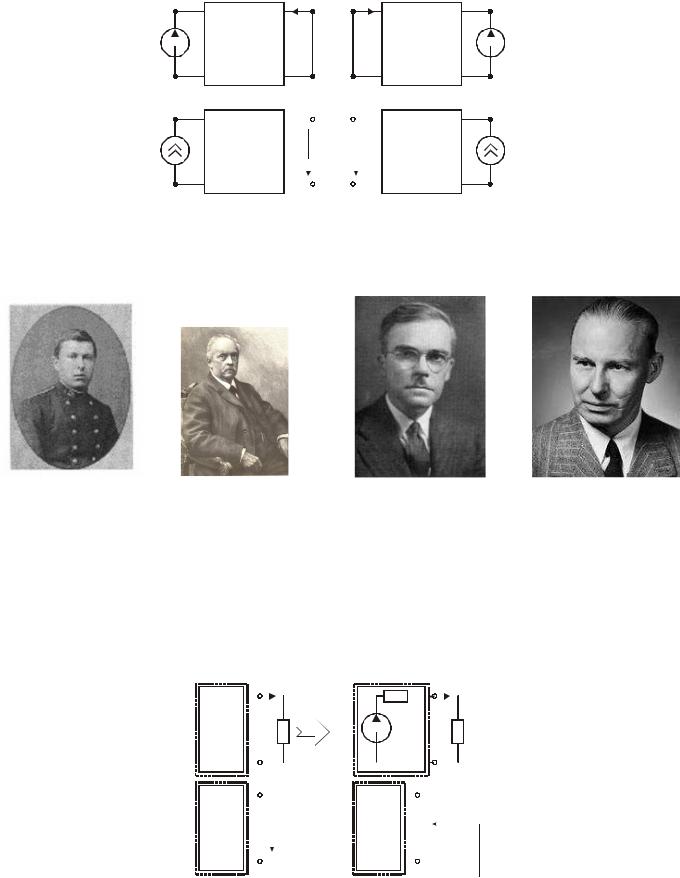
Теорема замещения: любую ветвь ЛЭЦ с напряжением u и током i можно заменить
источником напряжения с Eист = u и источником тока с Jист = i .
	i		i			i
ЛЭЦ u		ЛЭЦ u		ЛЭЦ		u


	R			Eист			Jист
	R			Eист			Jист

Теорема взаимности: если источник напряжения, включённый в некоторую ветвь ЛЭЦ, составленной из пассивных двухполюсников, вызывает в другой ветви этой цепи некоторый ток, то тот же источник напряжения, будучи перенесён в эту вторую ветвь, вызовет в первой ветви прежний ток.

12 /102

i 2

1 i

пассивная

цепь

Eист

1’

2’

1’

2’

пассивная

Jист

цепь

Jист

1’

2’

1’

2’

Теорема об активном двухполюснике. Теорема Тевенина-Гельмгольца. Теорема Майера-Нортона.

Леон Шарль Тевенин	Герман Людвиг	Эдвард Нортон (Edward	Ганс Фердинанд Майер
(Léon Charles Thévenin),	Фердинанд Гельмгольц	Lawry Norton), 1898-1983,	(Hans Ferdinand Mayer),
1857-1926, французский	(Hermann von Helmholtz),	американский учёный и	1895-1980, немецкий
телеграфный инженер	1821-1894, немецкий	инженер	математик и физик
	физик, физиолог и
	психолог

Теорема об активном двухполюснике используется в случае, когда надо найти реакцию цепи (ток или напряжение) в одной ветви. При этом остальную часть цепи, к которой подключена данная ветвь, удобно рассматривать в виде двухполюсника. Активный двухполюсник – содержит источники электрической энергии, в противном случае двухполюсник пассивный.

Различают две модификации теоремы об активном двухполюснике:

Теорема об эквивалентном источнике напряжения (Теорема Тевенина-Гельмгольца): ток в любой ветви ЛЭЦ не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником напряжения (ЭДС) с напряжением (ЭДС), равным напряжению холостого хода на зажимах разомкнутой ветви и внутренним сопротивлением источника, равным эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви.

Rист

Rэкв=Rист

Uхх=Eист

Теорема об эквивалентном источнике тока (Теорема Майера-Нортона): ток в любой ветви ЛЭЦ не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником тока с током, равным току короткого замыкания этой ветви, и внутренней проводимостью, равной эквивалентной входной проводимости со стороны разомкнутой ветви.

13 /102

Gист

Jист

Gэкв=Gист

Iк.з.=Jист

Связь между эквивалентными источниками напряжения и тока выражается соотношениями:

E	= J		R	, J		= G	E	, G =	1	.	(29)
		ист			ист
ист			ист			ист	ист	ист	Rист

Принцип дуальности. Теорема Телледжена. Баланс мощности.

Бернард Телледжен

(Bernard D.H. Tellegen) 1900-1990, голландский инженер

Принцип дуальности: если для данной электрической цепи справедливы некоторые законы, уравнения или соотношения, то они будут справедливы и для дуальных величин в дуальной цепи. Приведем дуальные понятия:

1.Напряжение и ток (u и i)

2.Сопротивление и проводимость (R и G)

3.Индуктивность и ёмкость (L и C)

4.I и II законы Кирхгофа

5.Последовательное и параллельное соединения.

Теорема Телледжена: сумма произведений напряжений и токов всех ветвей цепи, удовлетворяющих законам Кирхгофа, равна нулю.

Nв
∑un in = 0 .		(30)
n=1
Баланс мощности: для любой замкнутой электрической цепи сумма		мощностей Pист ,
развиваемых источниками электрической энергии, равна сумме мощностей		Pпот , расходуемой
в приёмниках энергии.
Pист = ∑ Pпот , или ∑(Ek Ik + UJk	Jk ) = ∑ Ik2 Rk .	(31)
k	k

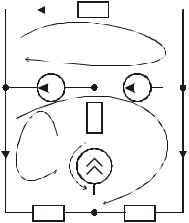
E I + UJ J = I12 R1 + I22 R2 + I32 R3 + I42 R4 , где UJ = E + I2 R2 .

R1 I1

	E				R3 I3
			I		R3 I3
R2						R4
R2		UJ		J



I2					I4
I2					I4

14 /102

Метод токов ветвей и метод контурных токов (МТВ и МКТ).

Метод токов ветвей (МТВ) основан на законах Кирхгофа. Число уравнений по МТВ равно

количеству неизвестных токов ветвей и определяется как:
Nмтв = Nв − NJ .	(32)
Количество уравнений, составляемых по I закону Кирхгофа, равно:
NI = Nуз −1.	(33)
Количество уравнений, составляемых по II закону Кирхгофа, равно:
NII = Nв − Nуз +1− NJ .	(34)
При составлении уравнений по II закону Кирхгофа следует выбирать независимые контуры,
не содержащие источников тока.
Метод контурных токов (МКТ) позволяет уменьшить количество уравнений до числа:
Nмкт = Nв − Nуз +1− NJ .	(35)

Ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви.

Выбирают и обозначают известные и неизвестные контурные токи.

Известные контурные токи – эти токи можно считать совпадающими с соответствующими токами источников тока, и они являются заданными по условию задачи.

Неизвестные контурные токи определяются по II закону Кирхгофа и для них составляется система уравнений в виде:

R11 I11 + R12 I22 +…+ R1k Ikk +…+ ∑ Jn Rn = E11; 1

R21 I11 + R22 I22 +…+ R2k Ikk +…+ ∑ Jn Rn = E22 ;

2	(36)

Rk1 I11 + Rk 2 I22 +…+ Rkk Ikk +…+ ∑ Jn Rn = Ekk ;
n
где Rkk – собственное сопротивление контура k; Rkm –	общее сопротивление контуров k и m,

причём, если направление контурных токов в общей ветви для контуров k и m совпадают, то

Rkm > 0 ,

в противном случае

Rkm < 0 ; Ekk –

алгебраическая сумма ЭДС, включённых в ветви,

образующие контур k; Rn –

общее сопротивление ветви контура n с контуром, содержащим

источник тока.

I11

J11

I22

I11 , I22 –

неизвестные контурные токи;

R3 UJ

J11 = J –

известный контурный ток;

I1 , I3 , I4

– неизвестные токи в ветвях, которые определяются через контурные токи в виде:

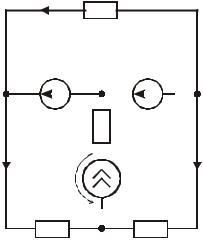
I1 = −I11, I3 = J11 − I22 , I4 = I22 .

Nмкт = Nв − Nуз +1− NJ = 6 − 4 +1−1 = 2

Система уравнений для контурных токов:

Nмун

15 /102

R11 I11 + R12 I22 + ∑ R J = E11, 1

R21 I11 + R22 I22 + ∑ R J = E22 , 2

где R11 = R1, R12 = R21 = 0, R22 = R3 + R4 , ∑ RJ = 0, ∑ RJ = −R3 J11, E11 = E1 + E2 , E22 = −E1 − E2 .

Перепишем уравнения в компактном виде:

R1 I11 = E1 + E2 ,

( R3 + R4 ) I22 − R3 J11 = −E1 − E2 .

Окончательно получаем:

I = −I = −

E1 + E2

(А), I

= J

− I

J R4 + E1 + E2

(А), I

= I

R3 J − E1 − E2

(А).

R3 + R4

+ R4

Метод узловых напряжений (МУН).

Метод узловых напряжений (МУН) позволяет уменьшить количество уравнений до числа:

Nмун = Nуз −1− NЕ .

(37)

Сущность метода: определяются потенциалы всех узлов, а токи ветвей, соединяющих узлы, находят с помощью закона Ома по формуле (17). При составлении уравнений по МУН вначале полагают равным нулю потенциал какого-либо узла (его называют базисным). Для определения потенциалов оставшихся узлов составляется система уравнений вида:

V1 G11 −V2 G12 −…−Vs G1s −…−Vn G1n = ∑ E G + ∑ J ;

	1	1
	−V1 G21 + V2 G22 −…−Vs G2 s −…−Vn G2n = ∑ E G + ∑ J ;			(38)
		2	2	(38)

	−V1 Gn1 −V2 Gn 2 −…−Vs Gns −…+ Vn Gnn = ∑ E G + ∑ J ;
		n	n
Здесь Gss	– сумма проводимостей ветвей, присоединенных		к узлу s; Gsq –	сумма
проводимостей ветвей, непосредственно соединяющих узел s с узлом q.
∑E×G –	алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу s, на их

проводимости; при этом со знаком "+" берутся те ЭДС, которые действуют в направлении узла, и со знаком "–" – в направлении от узла; ∑J – алгебраическая сумма токов источников тока,

присоединённых к узлу s; при этом со знаком "+" берутся те токи, которые направлены к узлу s, а со знаком "–" – в направлении от узла s.

I1 R1

E1 4

E2 3

Определим количество уравнений по МУН:

= Nуз −1− NЕ = 4 −1− 2 = 1

За базисный принимаем узел 4, из чего следует:

16 /102

V4 = 0 –

потенциал узла 4;

V2 = E1 –

потенциал узла 2;

V3 = −E2

–

потенциал узла 3;

Составим уравнение вида (38) для определения V1 :

V1 G11 −V2 G12 −V3 G13 = ∑ E G + ∑ J .

Определим неизвестные коэффициенты нашего уравнения:

G =

– проводимость ветвей, присоединённых к узлу 1;

–

проводимость ветви, заключённой между узлами 1 и 2;

–

проводимость ветви, заключённой между узлами 1 и 3;

∑ E G = 0 , поскольку нет ветвей с ЭДС, примыкающих к узлу 1;

∑ J = −J , поскольку ток источника тока направлен от узла;

После подстановки всех величин получаем уравнение в виде:

− E1

+ E2

= −J .

Из последнего уравнения определяем неизвестный потенциал V1

(единица измерения – вольт).

На следующем этапе определяем с помощью законов Ома неизвестные токи в ветвях:

I =

V3 −V2

−E2 − E1

(А), I

V2 −V1

(А), I

V3 −V1

(А).

Расчёт токов ветвей методом узловых напряжений с помощью матричных

уравнений

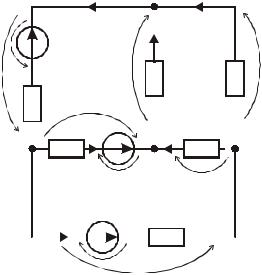
Пример 1. На рисунке изображена электрическая схема с шестью неизвестными токами;

UE1

UE2

UE3

ЭДС источников E1 = 6 В, E2 = 12 В и E3 = 18 В ; сопротивления ветвей: r1 = r2 = r3 = 2 Ом и r4 = r5 = r6 = 6 Ом . Пользуясь методом узловых потенциалов, определить токи в ветвях.

Решение. Пусть потенциал узла 0 равен нулю. Запишем уравнения с потенциалами ϕ1 , ϕ2 и ϕ3 :

( g1 + g2 + g3 )ϕ1 − g2ϕ2 − g3ϕ3 = −E1 g1 − E2 g2 − E3 g3 ;

−g2ϕ1 + ( g2 + g5 + g6 )ϕ2 − g5ϕ3 = E2 g2 ;

−g3ϕ1 − g5ϕ2 + ( g3 + g4 + g5 )ϕ3 = E3 g3 ,

17 /102

или после подстановки числовых значений проводимостей и ЭДС

3	ϕ −	1	ϕ		−	1	ϕ		= −18;	−	1	ϕ +	5	ϕ		−	1	ϕ		= 6;	−	1	ϕ −	1	ϕ		+	5	ϕ		= 9.
2		2											6											6
	1			2	2			3		2		1			2	6			3		2		1			2	6			3

Решая совместно эти уравнения, находим искомые потенциалы: ϕ1 = −9 В ; ϕ2 = 3 В ; ϕ3 = 6 В . Для

определения токов в ветвях следует задаться из положительными направлениями. При выбранных положительных направлениях токов

I1 = (ϕ0 − ϕ1 − E1 ) g1 = 1, 5 А ; I2 = (ϕ1 − ϕ2 + E2 ) g2 = 0 А ; I3 = (ϕ1 − ϕ3 + E3 ) g3 = 1, 5 А ; I4 = (ϕ3 − ϕ0 ) g4 = 1 А ; I5 = (ϕ3 − ϕ2 ) g5 = 0, 5 А ; I6 = (ϕ2 − ϕ0 ) g6 = 0, 5 А .

Матричные уравнения узловых потенциалов.

Уравнения узловых потенциалов

y +1

g11ϕ1 − g12ϕ2 −…− g1 p ϕ p −…− g1 y ϕy = J1 + ∑ E1 j g1 j = Jc1;

j=2

j¹1

y +1

ϕ2 −…− g2 p ϕ p −…− g2 y ϕy

= J2 + ∑ E2 j g2 j = Jc 2 ;

−g21ϕ1 + g22

j =1

j ¹2

…………………………………………………………………

y +1

−g p1ϕ1 − g p 2ϕ2 −…+ g pp ϕ p −…− g py ϕy = J p + ∑ Epj g pj = Jcp ;

j =1

j ¹ p

…………………………………………………………………

y +1

−g y1ϕ1 − g y 2ϕ2 −…− g yp ϕp −…+ g yy ϕy

= J y + ∑ Eyj g yj = Jcy ;

j =1

j ¹ y

можно записать в матричной форме:

g( y )ϕ = Jc ,

(1)

где

−g12

… −g1y

g11

g( y ) =

−g21

g22

… −g2 y

–

квадратная матрица проводимостей схемы;

…

… …

−g y1

−g y 2

… g yy

ϕ1

Jc1

ϕ =

и Jc

– матрица-столбец потенциалов узлов и матрица-столбец токов источников

…

ϕy

Jcy

тока

узлах, где

(по

общей формуле для любого узла p при ϕy+1 = 0 :

y+1

y +1

g pp ϕ p −∑ g pj ϕ j =J p +∑ Epj g pj =Jcp )

j =1

j=1

j ¹ p

j¹ p

Jci = Ji

+ ∑ Eij gij ;

при этом

алгебраическое суммирование, выполняемое с учётом знаков,

распространяется на все ветви с источниками токов и с источниками напряжений, присоединённые к i-му узлу.

Умножая уравнение (1) на

g( y )

-1

, получим выражение для определения потенциалов узлов

схемы в виде ϕ =

g( y )

-1

Jc , где

g( y )

-1

–

матрица, обратная матрице

g( y)

Матрицу узловых проводимостей цепи можно составить непосредственно по соответствующей схеме, применяя формулу

18 /102

g( y ) = Agd AT ,

(2)

где A – матрица соединения узловых проводимостей ветвей схемы или её ориентированного графа; gd – диагональная матрица проводимостей ветвей; AT – транспонированная матрица

соединения узловых проводимостей ветвей схемы или её ориентированного графа.

Матрица A составляется следующим образом: столбцы матрицы соответствуют ветвям схемы, а её строки – узлам; на пересечении строки и столбца записывается ±1 или 0 (пробел) в зависимости от того, присоединена данная ветвь к соответствующему узлу или нет; положительный знак записывается в том случае, когда ветвь направлена от узла, а отрицательный

– к узлу; при этом направление ветви обычно совмещается с положительным направлением тока в ней.

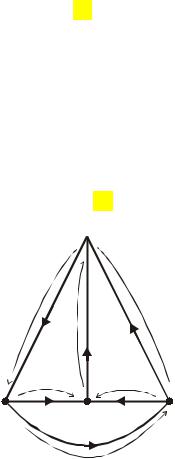
Для иллюстрации применения формулы (2) рассмотрим вышеприведённую схему, для которой построим ориентированный граф.

1	U2	U5	3
1			3
		2	U3
			U3

Поскольку у заданной схемы четыре узла, то для неё можно составить три независимых уравнения, чему и соответствует матрица соединения узловых проводимостей ветвей из трёх

	−1	1		1	0		0			0
	−1	1		1	0		0			0
строк и шести столбцов: A =	0	−1		0	0		−1			1			.
	0	0		−1	1		1			0
																			g1	0	0	0		0	0
																			g1	0	0	0		0	0
																			0	g2	0	0		0	0
Диагональная матрица проводимостей ветвей g									=	1				равна:		g		=	0	0	g3	0		0	0	.
								k									d		0	0	0	g4		0	0
											rk


																			0	0	0	0		g5	0
																			0	0	0	0		0	g6
						−g1				g2					g3	0			0	0
						−g1				g2					g3	0			0	0
Произведение матриц A и gd равно: Agd					=		0		−g2						0	0			−g5	g6	.
							0			0					−g3	g4			g5	0
Матрица узловых проводимостей цепи получается после перемножения матриц Ag																							d	и AT :
																			−1				d
																				0	0
																				0	0
			−g1		g2		g3						0		0		0		1	−1	0
																			1	−1	0
g( y ) = Agd AT =																			1	0	−1
			0	−g2				0					0 −g5				g6		1	0	−1	.
			0	−g2				0					0 −g5				g6		0	0	1	.
			0		0		−g3					g4			g5		0		0	0	1
			0		0		−g3					g4			g5		0		0	−1	1
																			0	−1	1
																			0	1	0

ϕ1

/102

Матрица-столбец потенциалов узлов ϕ =

ϕ2

ϕ3

матрица-столбец источников тока Jc

−E1 g1 − E2 g2 − E3 g3

E2 g2

E3 g3

Пользуясь выражением

(1), легко получить систему уравнений, приведённую в примере 1.

Если матрицу A дополнить

четвёртой строкой, соответствующей узлу 0, то по формуле

(2)

получится неопределённая матрица узловых проводимостей цепи, для которой сумма элементов

по всем четырём строкам и четырём столбцам равна нулю; определитель такой матрицы тоже

равен нулю. После вычёркивания любой строки и соответствующего этой строке столбца,

например четвёртой строки и четвёртого столбца, получается определённая квадратная матрица

третьего порядка. Определитель такой матрицы симметричен относительно главной диагонали.

Если вычеркнутая строка не соответствует вычеркнутому столбцу, то и в этом случае получается

определённая квадратная матрица, соответствующая независимой системе уравнений. Однако

определитель такой матрицы уже не имеет симметрии относительно главной диагонали. Если

принять равным нулю потенциал того же узла схемы , который соответствует вычеркнутой строке

матрицы A, то напряжения на всех ветвях схемы определяются через потенциалы узлов по

формуле Uв = AT ϕ , где положительное

направление Uв совпадает

с положительным

направлением тока в ветви. Это непосредственно получается из формул для напряжения на

каждой ветви. Например, для вышеприведённой схемы

−ϕ1

−1

ϕ1

ϕ1 − ϕ2

1 0 −1

ϕ1 − ϕ3

ϕ2

ϕ3

−1

−ϕ2 + ϕ3

ϕ2

Из этого выражения следует: U1 = −ϕ1 ; U2

= ϕ1 − ϕ2 ; U3 = ϕ1 − ϕ3 ; U4 = ϕ3 ; U5

= ϕ3 − ϕ2 ; U6 = ϕ2 .

Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С. В. Основы теории цепей. Учебник для вузов. Изд. 4-е, пер. М., «Энергия», 1975. 752 с. Стр. 41-44.

Расчёт токов ветвей методом контурных токов с помощью матричных уравнений

Уравнения контурных токов

r11I1 + r12 I2 +…+ r1l Il +…+ r1k Ik = E1;
r I + r I				+…+ r I		+…+ r I		= E ;
21 1	22 2			2l l		2k k		2

……………………………………………
r I + r		I		+…+ r I	+…+ r I		= E ;
l1 1	l 2		2	ll l		lk k		l
……………………………………………
	+ r		I	+…+ r I		+…+ r I		= E ;
r I
k1 1	k 2		2	kl l		kk k		k
с учётом

				+ ∑ rlj I j	= El + ∑rlj Jlj = Ecl ,
			∑ rlj Il	+ ∑ rlj I j	= El + ∑rlj Jlj = Ecl ,
			j	j	j
				j¹l
		обозначают собственное сопротивление контура l;
где	∑ rlj	обозначают собственное сопротивление контура l;
	j

rlj – общее сопротивление двух контуров l и j;

Jlj – ток источника тока, замыкающийся по сопротивлению rlj , можно записать в матричной форме:

20 /102

r(k )Ι(k ) = Ε(ck )

(3)

где r(k ) – квадратная матрица контурных сопротивлений; Ι(k ) – матрица-столбец контурных токов;

Ε(ck ) – матрица-столбец контурных ЭДС, учитывающая источники ЭДС и эквивалентные ЭДС от источников тока.

После умножения уравнения (3) слева на r(k ) −1 получим:

Ι(k ) = r(k ) −1 Ε(ck ) .

Матрицу контурных сопротивлений r(k ) можно получить непосредственно по схеме при помощи матрицы соединения контурных сопротивлений B :

	r(k ) = Br BT ,		(4)
	d
где rd	– диагональная матрица сопротивлений ветвей;
BT –	транспонированная матрица соединения контурных сопротивлений.
	Матрица соединения контурных сопротивлений B составляется так, что её строки
соответствуют независимым контурам, а столбцы – ветвям.		На пересечении строки и столбца

записывается ±1 или 0 (пробел) в зависимости от того, входит или не входит данная ветвь в соответствующий контур; положительный знак принимается в том случае, если направление ветви совпадает с направлением обхода контура, а отрицательный знак – если не совпадает. При этом направление обхода каждого контура принимается совпадающим с положительным направлением соответствующего контурного тока, а направления ветвей – с положительными направлениями токов в ветвях.

Для получения независимых контуров следует сначала выбрать дерево схемы, что в свою очередь определяет ветви связи, а следовательно, и контурные токи. Для составления дерева схемы выбирается узел (в котором, желательно, соединяется максимальное число ветвей), а затем выбираются все остальные ветви, так, чтобы не было замкнутых контуров, но чтобы в итоге соединить все узлы.

Для иллюстрации на рисунке приведена схема с выбранным деревом из четвёртой, пятой и шестой ветвей.

UE1

I1к

I2к

UE2

UE4

I3к

UE3

В этом случае независимые контуры

содержат

контурные токи I1 , I2 и I3 , что

соответствует первой, второй и третьей ветвям связи.

Для вышеприведённой схемы построим ориентированный граф.

<<< < Предыдущая 12 / 112 3 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.201958.88 Кб3ТЭИС темы,вопросы,литер..doc
#
10.11.2019210.94 Кб5ТЭИС. мет.КР.doc
#
22.08.201984.48 Кб4ТЭО-ПС-09.doc
#
10.06.20151.21 Mб42ТЭЦ контр.doc
#
11.11.2019313.34 Кб8ТЭЦ курсовая ВАРИАНТЫ 11-14 группы.doc
#
10.06.20152.64 Mб112ТЭЦ Лекции.pdf
#
10.06.20153.35 Mб179УИП Методическое пособие 2014.docx
#
29.03.2016548.84 Кб833УИП_краткий курс_2013.docx
#
27.11.2019682.5 Кб7УМК ОЭ от 12.04 11г..doc
#
27.11.2019430.59 Кб8УМК по ОСиП.doc
#
25.11.201918.81 Mб91УП КП 20.12.11.doc