Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТЭЦ Лекции

.pdf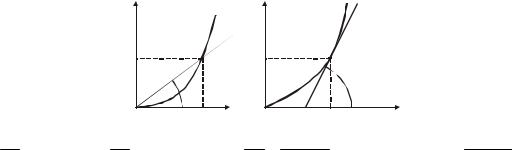

Скачиваний:

112

Добавлен:

10.06.2015

Размер:

2.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Определить статическое и дифференциальное сопротивление в точке u = U0 .

1.	Определяем значение тока, если u = U	0	: I	0	= a + a U						0	+ a		2	U	2 .
		0		0		0			1		0			2		0
2.	Определяем статическое сопротивление: R					=	U0		=						U0							.
2.	Определяем статическое сопротивление: R					=			=	a + a U							+ a					.
				ст			I													U 2
							I	0								0			2	U 2
								0			0			1		0			2		0
3.	Определяем дифференциальную проводимость: G										=		di					= a + 2 a U						0	.
													di

									диф				du		u =U0					1		2


4.	Определяем дифференциальное сопротивление: Rдиф										=		1			=					1		.

																			+
													Gдиф					a1	+		2 a2 U0

Данный способ является аналитическим. Рассмотрим графический способ статического и дифференциального сопротивления.

U1 U0

u = U0 −U1

= I0

= tg α , R

= U0

= ctg α .

i =

= tg β , R

ст

диф

u U

0 −U1

диф

61 /102

определения

= ctg β .

Нелинейные реактивные элементы

К нелинейным реактивным элементам относят:

Нелинейные индуктивные элементы – катушки с ферромагнитными сердечниками. Ферромагнитные материалы являются сплавами на основе металлов группы железа или их оксидов – ферритов. Нелинейность обусловлена характеристикой намагниченности материала

сердечника B (H ) . Поскольку магнитный поток	Φ пропорционален индукции B, Φ = B S , а
напряжённость H связана с током i в обмотке,	имеющей w витков: H =	iw	, где S – сечение

		l
сердечника, l – длина сердечника, то вид зависимости предопределяет характер вебер-амперной

характеристики Ψ (i) , где потокосцепление обмотки Ψ = Φ w .

Виды магнитных материалов: магнитотвёрдые материалы, магнитомягкие материалы, магнитострикционные материалы, магнитооптические материалы, термомагнитные материалы.

Магнитотвердые материалы применяют для производства постоянных магнитов. Они являются источниками постоянных магнитных полей, используемых в различной аппаратуре в электро- и радиотехнике, автоматике, приборостроении, электронике, в устройствах электромагнитной записи, фокусирующих устройствах для телевизоров, микрофонах, электроизмерительных приборах, микроэлектронике, СВЧ-приборах и т.д. Их используют в электрических машинах малой мощности, для записи и хранения цифровой, звуковой и видеоинформации и др. Преимущества постоянных магнитов по сравнению с электромагнитами постоянного тока – повышенная работоспособность; экономия материалов и потребления энергии; экономическая и техническая выгода применения.

Магнитомягкие материалы используются в качестве сердечников трансформаторов, электромагнитов, в измерительных приборах и в других случаях, где необходимо при наименьшей затрате энергии достигнуть наибольшей индукции. Магнитомягкие материалы с повышенным удельным электрическим сопротивлением используются в трансформаторах для уменьшения потерь на вихревые токи.

Магнитострикция (от магнит и лат. strictio — сжатие, натягивание), изменение формы и размеров тела при его намагничивании. Магнитострикция в области технического намагничивания обнаруживает явление гистерезиса. Магнитострикция используется, например, для получения ультразвука 2·104...109 и гиперзвука 109...1013 Гц.

Магнитооптические материалы. Наведённая магнитным полем оптическая активность проявляется в двух эффектах – Фарадея и Керра. Эффект Фарадея сводится к повороту плоскости линейной поляризации светового луча, проходящего через магнитооптическую среду. Угол поворота при направлении магнитного поля вдоль луча пропорционален напряженности магнитного поля. Нечто похожее наблюдается и при отражении линейно поляризованного луча света от поверхности ферромагнитного материала в присутствии магнитного поля. Этот эффект именуют эффектом Керра. Прошедший или отраженный свет несет, таким образом, информацию о текущем значении напряженности магнитного поля на поверхности ферромагнитного материала, зафиксированную углом поворота плоскости поляризации луча. Магнитооптические эффекты применяются при считывании информации с магнитооптических дисков. Из других магнитооптических устройств можно выделить оптические запоминающие устройства, магнитооптические устройства сканирования света и ряд других.

62 /102

Термомагнитные материалы – ферромагнитные сплавы с сильной зависимостью намагниченности насыщения от температуры в заданном магнитном поле. Применяют в качестве магнитных шунтов или магнитных добавочных сопротивлений для компенсации изменения магнитного потока в цепи, вызванные температурными изменениями электрического сопротивления обмоток магнита, величины воздушного зазора магнита и т. д. Применяются в реле, момент срабатывания которых зависит от температуры.

Статическое электромагнитное устройство, предназначенное для использования его индуктивности в электрической цепи, называют реактором.

На электропитающих сетях переменного и постоянного тока и на тепловозах широко применяют реакторы: сглаживающие — для сглаживания пульсаций выпрямленного тока; переходные — для переключения выводов трансформатора; делительные — для равномерного распределения тока нагрузки между параллельно включенными вентилями; токоограничивающие

— для ограничения тока короткого замыкания; помехоподавления — для подавления радиопомех, возникающих при работе электрических машин и аппаратов; индуктивные шунты — для распределения при переходных процессах тока между обмотками возбуждения тяговых двигателей и включенными параллельно им резисторами и пр.

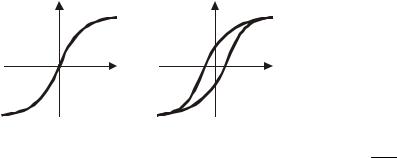
Примеры вебер-амперных характеристик: слева обычная вебер-амперная характеристика, а справа эта зависимость носит гистерезисный характер. Такая зависимость возникает при циклическом намагничивании сердечника.

Гистере?зис(греческое ὑστέρησις – «отстающий») – свойство систем, которые не сразу следуют приложенным силам. Реакция этих систем зависит от сил, действовавших ранее, то есть системы зависят от собственной истории.

Магнитный гистерезис – явление зависимости вектора намагничивания и вектора напряжённости магнитного поля в веществе не только от приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется в ферромагнетиках – Fe, Co, Ni и сплавах на их основе. Именно магнитным гистерезисом объясняется существование постоянных магнитов.

Нелинейный индуктивный элемент характеризуется:

Статической индуктивностью Lст = Ψ , дифференциальной индуктивностью i

Lдиф = d Ψ ,

d i

которые зависят от намагничивающего тока i.

Нелинейные ёмкостные элементы. Например, вариконд, – электрический конденсатор с диэлектриком из специального сегнетокерамического материала, обладающего свойством резко изменять диэлектрическую проницаемость ε при изменении напряжённости электрического поля E. Электрическая ёмкость таких конденсаторов под воздействием приложенного к ним электрического напряжения может изменяться в 4…6 раз.

При увеличении напряжения ёмкость варикондов возрастает, достигает максимального значения и затем снижается. Это свойство позволяет применять вариконды в качестве усилителей переменного и постоянного токов, умножителей частоты, стабилизаторов напряжения, генераторов напряжения, генераторов импульсов и других устройств.

Варикап – полупроводниковый диод, работа которого основана на зависимости барьерной ёмкости p-n перехода от обратного напряжения. Так как p-n-переход можно рассматривать как плоский конденсатор, обкладками которого служат области n- и p-типа вне перехода, а изолятором является область объемного заряда, обеднённая носителями заряда и имеющая большое сопротивление, то такую ёмкость называют барьерной.

Варикапы применяются в качестве элементов с электрически управляемой ёмкостью в схемах перестройки частоты колебательного контура, деления и умножения частоты, частотной модуляции, управляемых фазовращателей и др.

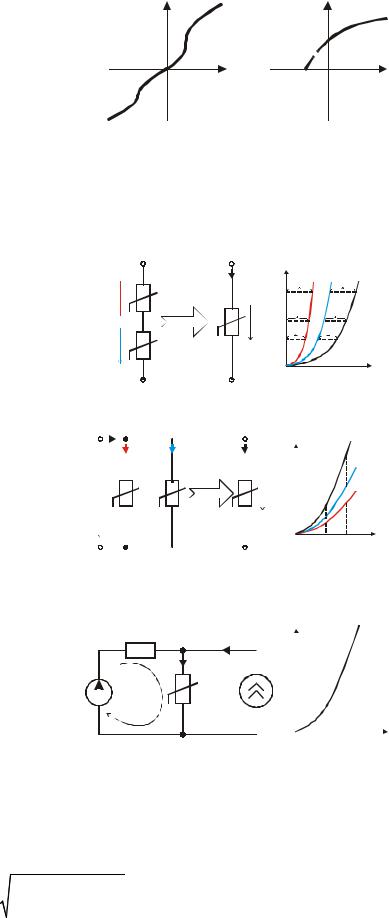
Нелинейные ёмкостные элементы описываются вольт-кулонной характеристикой (для вариконда – слева, для варикапа – справа).

63 /102

q	q
u	u

Нелинейный элемент ёмкости характеризуется статической и дифференциальной ёмкостью:

C =	q	, C		=	d q	,
			диф
ст	u				d u

которые зависят от приложенного напряжения u.

Методы расчёта нелинейных резистивных электрических цепей

Графо-аналитический метод расчёта НЭ Рассмотрим последовательное соединение нелинейных резистивных элементов:

i	НЭ1	i	i
u1			u
			u
u2	НЭ2	НЭ
	НЭ2		0	u
На основании II закона Кирхгофа: u = u1 + u2			0	u
На основании II закона Кирхгофа: u = u1 + u2		получаем ВАХ НЭ.

Рассмотрим параллельное соединение нелинейных резистивных элементов.

	i			i
		i1	i2		i
	u	НЭ1	НЭ2
	u				u
				НЭ		0




На основании I закона Кирхгофа: i = i1 + i2				получаем ВАХ НЭ.

Аналитический метод расчёта НЭ основан на законах Кирхгофа.

0,	Uнэ < 0
Iнэ =		.
αUнэ2		, Uнэ > 0

I R

IНЭ

НЭ

Находим решение, если Uнэ > 0 :

Iнэ = I + J , E = Uнэ + I R .

I = Iнэ − J , E −Uнэ − (αUнэ2 − J ) R = 0 .

После преобразований получим:

α RUнэ2 + Uнэ − ( J R + E ) = 0 .

Uнэ = −

J R + E

– первое решение.

α R

4 α2 R2

α R

Находим решение, если Uнэ < 0 :

I = −J , Uнэ = E + J R –

второе решение.

Второе решение противоречит условию Uнэ < 0 , поэтому оставляем первое решение.

64 /102

Если ВАХ НЭ описывалась более сложной функцией, то аналитическое решение получить было бы невозможно.

Аналитическое представление ВАХ

Точное представление ВАХ в аналитическом виде невозможно, поэтому на первое место выходит приближённое представление ВАХ (задача аппроксимации).

Задача аппроксимации состоит в двух этапах:

1.Выбор аппроксимирующей функции f ( x)

2.Выбор критерия оценки «близости» Λ в интервале аппроксимации a ≤ x ≤ b .

L = max f ( x) - x( x) , где x( x) – аппроксимируемая функция.

L = 1	b
	∫( f ( x) - x( x))2 dx .

b - a a

Виды аппроксимации Полиномиальная (степенная) аппроксимация

В качестве аппроксимирующей функции используются алгебраические полиномы: f ( x) = a0 + a1 x + a2 x2 +…+ an xn .

Добиваются совпадения значений аппроксимирующей и аппроксимируемой функций в возможно большем числе выбранных точек в интервале a ≤ x ≤ b . Соответствующий метод приближения называется интерполяция. Выбранные точки – узлы интерполирования их число на единицу превышает степень интерполирующего полинома, то есть

Nуз. инт. = n +1 .

Из условия f ( xk ) = x( xk ) , k = 0, 1,	2, …,		n получим n +1 систему линейных уравнений:
a + a x + a x2				+…+ a xn = x( x )
0	1 0	2 0		n 0		0
a + a x + a x2				+…+ a xn		= x( x )
0	1 1	2 1		n 1		1
…………………………………………
a + a x + a			x2	+…+ a	xn = x( x )
0	1 n		2 n		n n	n
Пример: интерполируем полиномом	f ( x)	= a		+ a x в интервале 0 ≤ x ≤ 2 функцию x( x) =1- e− x .
			0	1

1.Определяем число узлов интерполирования: Nуз. инт. = n +1 = 1+1 = 2 .

2.Выбираем значение узлов интерполяции: x0 = 0,1, x1 =1 .

3.Получим систему линейных уравнений:

1,5

1,2 f(x)

0,9ξ(x)

0,6

0,3
0 0	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8	2,0
a + a ×0,1 = 1- e−0,1
0	1			, откуда a0			= 0, 036 , a1 = 0, 597 .
a + a = 1- e−1				, откуда a0			= 0, 036 , a1 = 0, 597 .
a + a = 1- e−1
0	1				f ( x) = 0, 036 + 0, 597 x .
4. Аппроксимирующий полином имеет вид:					f ( x) = 0, 036 + 0, 597 x .

Наибольшее отклонение наблюдаем в точке x = 2 , а именно:

L = max f ( x) - x( x) = 0, 365

Точность аппроксимации увеличивается при увеличении степени полинома:

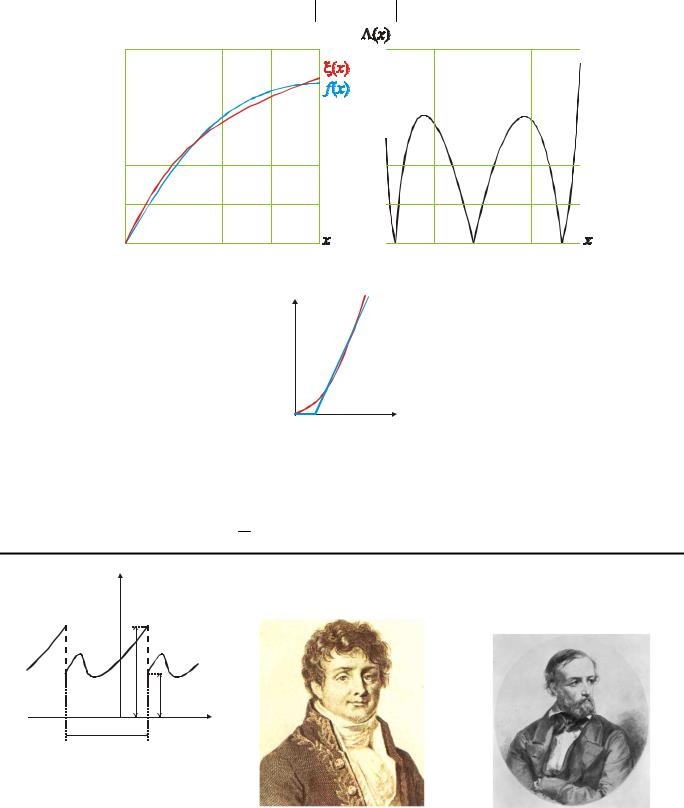
Пример: интерполируем полиномом f ( x) = a		+ a x + a		x2 в	интервале 0 ≤ x ≤ 2 функцию
x( x) = 1- e− x . Число узлов интерполяции: 3.	0	1	2
x( x) = 1- e− x . Число узлов интерполяции: 3.	x	= 0,1;	x	= 0,9;	x = 1,8;
	0		1		2

65 /102

	x0	2	−1	x( x0 )				0, 014
1	x0	x0		x( x0 )				0, 014
	x1	2					=		0,832	;
A = 1	x1	x1		× x( x1 )			=		0,832	;
1	x	x2		x( x		)			-0, 209
	2	2			2

a0 = 0, 014; a1 = 0,832;	a2	= -0, 209;	L ( x) = f ( x) - x( x) .
ξ(x), f (x)
1,0					0,025
0,8					0,020
0,6					0,015
0,4					0,010
0,2					0,005
0	0,5	1,0	1,5	2,0	0	0,5	1,0	1,5	2,0
0	0,5	1,0	1,5	2,0	0	0,5	1,0	1,5	2,0

Кусочно-линейная аппроксимация заключается в замене реальной ВАХ приближённой, состоящей из отрезков прямых линий, выбираемых касательными.

0,	при
i (u ) = S (u -U		0
		0

Аппроксимация

i
0	U0	u

u £ U0

), при u ³ U0

трансцендентными функциями (экспоненты, гиперболические и другие функции).

i (u ) = A(eα u -1) , i (u ) = A2 (1+ th a (u - B)) , где A, B, α – варьируемые параметры.

Негармонические периодические сигналы. Разложение в ряд Фурье

	f (t)
негармоническая f (t1−0)
функция
		f (t1+0)
0	t1	t
T

Жан Батист Жозеф Фурье (Jean	Ио&ганнПе&терГу&ставЛежён-
Baptiste Joseph Fourier) 1768-1830,	Дирихле&(Johann Peter Gustav
французский математик и физик	Lejeune Dirichlet)1805-1859,
	немецкий математик

Если	f (t )			– периодическая негармоническая функция, удовлетворяет условиям Дирихле, то её
можно разложить в ряд Фурье:
		a0		∞
f (t )	=		+ ∑(ak cos k wt + bk sin k wt ) . тригонометрическая форма

	2			k =1

66 /102

Функция f ( x) называется удовлетворяющей условиям Дирихле на интервале [a, b] , если она

1)непрерывна на [a, b] или имеет конечное число точек разрыва 1 рода (если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке);

2)кусочно монотонна на [a, b] , то есть отрезок [a, b] можно разделить на конечное число отрезков, внутри которых

функция f ( x) либо только возрастает, либо только убывает, либо постоянна.

Коэффициенты разложения определяются как:

t0 +T

ak =

t∫

f (t )cos k ωt dt , bk

t∫

f (t )sin k ωt dt .

f (t ) равны, то a0

= 0 .

Если площади положительных и отрицательных значений

t0 – может быть выбрано произвольно, далее полагаем t0

= 0 .

2 π

Для удобства введём переменную: α = ωt . Учитывая, что ω =

получим:

2 π

∞

f (α) =

+ ∑(ak cos k α + bk

sin k α) , где ak =

∫0

f (

α)cos k α dα , bk =

f (α)sin k α dα .

k =1

π ∫0

Если принять t0

= −

, то пределы интегрирования будут равны соответственно −π и +π .

Сумма гармоник в ряде Фурье может быть представлена в виде суммы только одних синусоид в виде функции косинуса с соответствующими начальными фазами. Для этого, пусть ak = Fk cos ψk ,

bk = Fk sin ψk . Подставляя в ряд Фурье, получим:

								a0	∞
							f (α) =	a0	+ ∑ Fk cos (k α − ψk ) , где
							f (α) =		+ ∑ Fk cos (k α − ψk ) , где
							2		k =1
F =
F =			a2	+ b2		–	амплитуда k-ой гармоники (амплитудный спектр),
k			k		k
ψ		= arctg			bk	–	начальная фаза k-ой гармоники (фазовый спектр).
ψ	k	= arctg			ak	–	начальная фаза k-ой гармоники (фазовый спектр).
	k

Представим ряд Фурье в комплексной форме:

ejk α + e− jk α

ejk α

− e− jk α

Поскольку: cos k α =

, sin k α =

2 j

= Fk cos ψk

– функция чётная, поэтому ak

= a− k ,

bk = Fk sin ψk

–

функция нечётная, поэтому bk

= −b− k , получаем:

f (α) =

∞

ejk α + e− jk α

ejk α − e− jk α

+ ∑ ak

− jbk

k =1

∞

∑(ak

− jbk )ejk α +

∑(ak + jbk )e− jk α =

2 k =1

∞

−1

∞

∑(ak

− jbk )ejk α +

∑ (ak

− jbk )ejk α =

∑

(ak − jbk )ejk α

2 k =1

2 k =−∞

f (α) =	1		∞
	1		∑ F k ejk α , где
			∑ F k ejk α , где
	2 k =−∞					∫
				π		∫
Поскольку a			=	1	2		π	f (α)cos k
Поскольку a			=		2			f (α)cos k
	k
						0				2 π
F			= a				− jb =		1
F			= a				− jb =
		k				k		k	π ∫
		k				k		k
									0

F k = ak − jbk = Fk e− jψk – комплексная амплитуда k-ой гармоники.

α dα , b =	1	2 π	f (α)sin k α dα , то
α dα , b =		2 π	f (α)sin k α dα , то
k	π ∫
k
	0				2 π			2 π
				1	2 π		1	2 π
f (α)cos k α dα − j				1	∫	f (α)sin k α dα =	1	∫ f (α)e− jk α dα .
f (α)cos k α dα − j				π	∫	f (α)sin k α dα =	π	∫ f (α)e− jk α dα .
				π	0		π	0
					0			0

После возвращения к переменной t, получим:

67 /102

F k =

∫ f (t )e− jk ωt dt , либо F k

∫ f (t )e− jk ωt dt –

формулы для комплексного спектра.

−

Свойства ряда Фурье

1. Функция

f (α) симметрична относительно оси ординат:

f (α)

−2

−1

f (α) =

∞

∑ ak cos k α .

k =1

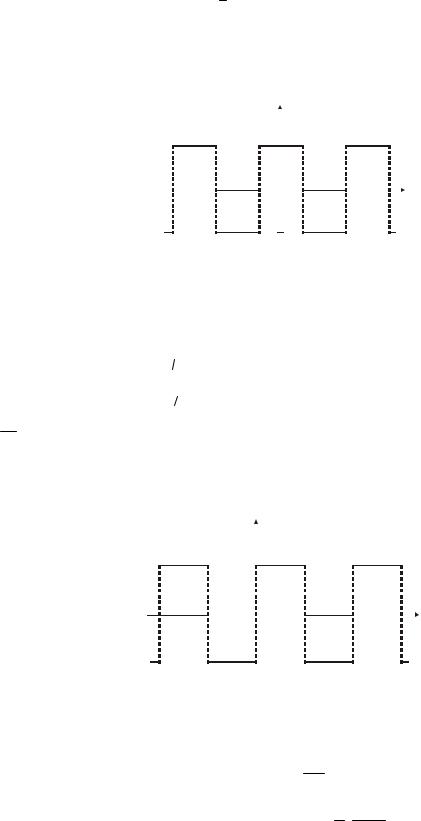
Разложим в ряд Фурье последовательность прямоугольных импульсов. Для определения коэффициентов достаточно пользоваться кривой f (α) за половину периода, то есть

f (α) = a0

π 2

k π

∫

1cos k α dα =

sin

, следовательно:

π k

∞

−π 2

cos α

cos 3α

+ ∑ ak cos k α =

cos α −

cos 3

α +

cos 5

α −…=

−

5 π

k =1

π 1

	cos 5 α
+		−… .
+	5	−… .
	5

Если функция симметрична относительно оси ординат, то разложение в ряд Фурье содержит только нечётные гармоники по закону косинуса.

2. Функция f (α) симметрична относительно начала координат:

	1		f (α)
			f (α)
−π				π		α







		0			2π
			−1

∞
f (α) = ∑bk sin k α .
k =1
b =	2	π	1sin k α dα = −	2	cos k α
	2			2

k	π ∫			π k
k
	0

=2 (1− cos π k ) , следовательно:

πk

∞		4		4		4
f (α) = ∑bk	sin k α =		sin α +		sin 3α +
				3 π		5 π
k =1		π

α − = 4 sin α sin 5 …

π 1

	sin 3α		sin 5 α
+		+		+… .
+	3	+	5	+… .
	3		5

Если функция симметрична относительно начала координат, то разложение в ряд Фурье содержит только нечётные гармоники по закону синуса.

3. При сдвиге начала отсчёта функции f (t ) её амплитудный спектр не изменяется, а меняется

только фазовый спектр.

Сдвинем функцию f (t )

по оси времени влево на t0 :

(

)

∞

cos

(

kω

(

t + t

0 )

− ψ

k )

∞

cos

(

kωt − ψ′

∑ k

k )

k =1

где ψ′

= ψ

− k ωt

/102

π влево

В свойстве (1) последовательность прямоугольных импульсов сдвинута на угол

относительно последовательности прямоугольных импульсов в свойстве (2), разложение которого

в ряд определяется как:

4 sin α

sin 3α

sin 5 α

f (α) =

… .

С учётом свойства (3) получим:

f (α)

4 sin

(α + π 2)

sin 3(α + π 2)

sin 5

(α + π 2)

4 cos α

−

cos 3α

cos 5 α

+…

−… .

С помощью свойства сдвига для функции, приведённой в свойстве (1) найдено её разложение в

ряд Фурье, с помощью найденного разложения в ряд Фурье функции, приведённой в свойстве (2).

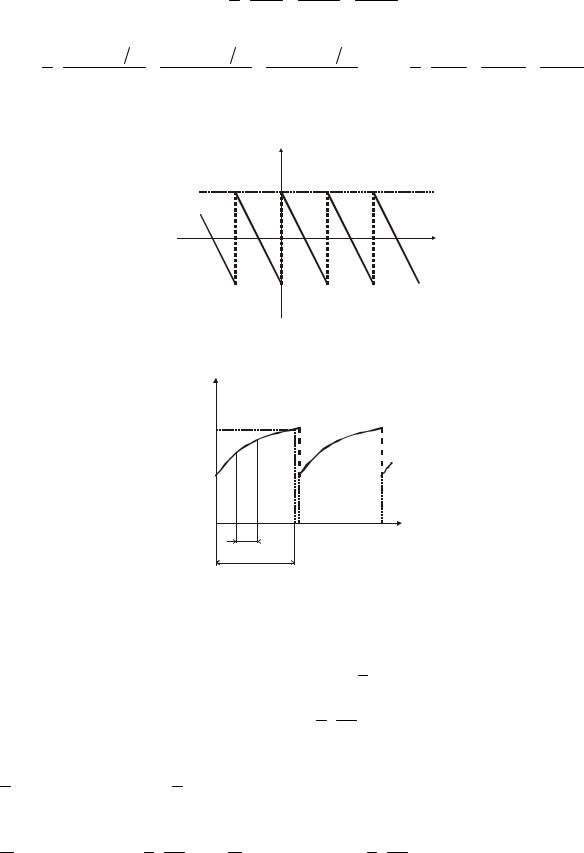
Самостоятельно разложить в ряд Фурье последовательность пилообразных импульсов

f (α)

−π

2π

−1

Графо-аналитический способ разложения в ряд Фурье

Данный способ применяется в случае, когда функция

f (α) имеет сложную форму.

f (α)

f (αn)

2π

αn

4π

f (α) , равный 2 π ,

Период функции

разбивается на m равных интервалов

α при этом выполняется:

m Δα = 2 π .

Расстояние от начала координат до середины n-го интервала:

αn

= n Δα −

Δα

n −

Δα ,

2 π

αn

n −

Коэффициенты ряда Фурье вычисляются как:

= 1 2 π

f (α)cos k α dα ,

= 1 2 π

f (α)sin k α dα .

∫

π ∫

Интегралы заменяем конечной суммой:

≈

2 π

2 m

−

1 2 π

∑ f

(αn )cos k n −

, bk ≈

∑ f

(αn )sin k n

m n=1

2 m

69 /102

Последние два уравнения легко программируются, и при вычислении коэффициентов может использоваться ЭВМ.

Действующее, среднее значение и мощность периодического негармонического

сигнала

Действующее значение определяется как

I = 1 ∫i2 (t ) dt , U = T 0

1 ∫u2 (t ) dt . T 0

Мгновенные значения периодических негармонических изменений тока и напряжения:

∞

i (t ) = I0 + ∑ Imk cos (k ωt − ψik )

, u (t ) = U0 + ∑Umk cos (k ωt − ψuk ) .

k =1

Таким образом, получаем:

∞ 2

∞

I = I02 + ∑

Imk

= I02 + ∑ Ik2 =

∑ Ik2 ,

U = U02 + ∑

Umk

= U

02 + ∑Uk2 =

∑Uk2 .

k =1 2

k =1

k =0

k =1

k =0

Вывод: действующее значение периодического негармонического сигнала определяется действующими значениями его гармоник и не зависит от их начальных фаз.

Среднее значение периодического негармонического сигнала определяется как:

	1	T	1	T
< I >=		∫i (t ) dt , < U >=		∫u (t ) dt .
	T		T
		0		0

Активная мощность негармонического сигнала: P = 1 ∫u (t )i (t ) dt T 0

Мгновенные значения представим как:

∞	∞
i (t ) = ∑ Imk cos (k ωt − ψik ) , u (t ) = ∑Umk cos (k ωt − ψik + ϕk ) ,
k =0	k =0

где ϕk – фазовый сдвиг между током и напряжением k-ой гармоники. Выражение для активной мощности будет в виде:

∞		∞
P = ∑Uk Ik cos ϕk		= ∑ Pk [Вт].
k =	0	k =0

Вывод: средняя за период активная мощность периодического негармонического сигнала равна сумме мощностей отдельных гармоник.

Реактивная мощность и полная мощность периодического негармонического сигнала определяются соответственно:

∞	∞	∞	∞
Q = ∑Uk Ik sin ϕk	= ∑Qk [ВАр], S = U I =	∑Uk2	∑ Ik2 [ВА].
k =0	k =0	k =0	k =0

Для периодических негармонических сигналов: S = 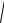P2 + Pиск2 + Q2 , где Pиск – мощность искажений.

Характеристики формы периодических негармонических сигналов

Периодические негармонические сигналы характеризуются рядом коэффициентов: 1. Коэффициент формы – отношение действующего значения к среднему значению:

kф =	I		=	U	.
	< I	>		< U >

2. Коэффициент амплитуды – отношение максимального значения к действующему значению:

ka	=	Imax	=	Umax	.
		I
				U

3. Коэффициент искажения – отношение действующего значения первой (основной) гармоники к действующему значению всего сигнала.

kи = I1 = U1 . I U

70 /102

4. Коэффициент

гармоник

–

отношение

действующего

значения

высших

гармоник

к действующему значению основной гармоники.

∞

∑ Ik2

∑Uk2

kг = k =2

= k =2 .

Пусть задано периодическое негармоническое колебание вида:

u (t ) = Um1 sin wt +Um2 sin 2 wt , причём Um1 =10 B , Um2 = 5 B .

∞

Определим действующее значение по формуле: U =

U02 + ∑Umk

Um1 + Um2

= 7, 906 B .

k =1

Для удобства анализа используем переменную α = ωt , тогда

u (a) = Um1 sin a +Um2 sin 2 a = u1 (a) + u2 (a) .

Представим графики u (a) ,

u1 (a)

и u2 (a) :

u(α), u1(α), u2 (α)

90°

180°

270°

360°

−5

u(α)

−10

−15

0,5

1,0

1,5

2,0

Определим среднее значение напряжения u (a) по формуле:

< U >= 1 π (Um1 sin a +Um2 sin 2a) da =

2Um1

= 6,366 B .

p ∫0

Таким образом, коэффициент формы определяется как: kф =

7, 906

= 1, 242 .

< U >

6,366

Определим максимальное напряжение:

	d u	= Um1 cos a + 2Um 2 cos 2 a = 0 , поскольку cos 2 a = 2 cos2 a -1, то
	d a
				(			-Um1 )= 0, 5 .
			1
4Um 2 cos2 a +Um1 cos a - 2Um 2 = 0 , cos a =					Um12 + 32Um2	2

			8Um 2

Следовательно, a = arccos (0, 5) = 600 и максимальное напряжение вычисляется как:

Umax = Um1 sin 60o +Um 2 sin120o = 12, 99 B .

Таким образом, коэффициент амплитуды определяется как: ka

Umax

12,99

= 1, 643 .

7, 906

Определим коэффициент искажения: kи

Um1

= 0,894 .

7, 906 ×

U U

∞

∑Uk2

Um2

Определим коэффициент гармоник: kг =

k =2

= 0,5

Um1

Расчёт цепей при периодических негармонических воздействиях

При периодическом негармоническом воздействии расчёт токов (напряжений) производится для каждой из гармоник отдельно по ранее изученным методам расчёта цепей. После этого определяется результирующая реакция.

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.201958.88 Кб3ТЭИС темы,вопросы,литер..doc
#
10.11.2019210.94 Кб5ТЭИС. мет.КР.doc
#
22.08.201984.48 Кб4ТЭО-ПС-09.doc
#
10.06.20151.21 Mб42ТЭЦ контр.doc
#
11.11.2019313.34 Кб8ТЭЦ курсовая ВАРИАНТЫ 11-14 группы.doc
#
10.06.20152.64 Mб112ТЭЦ Лекции.pdf
#
10.06.20153.35 Mб179УИП Методическое пособие 2014.docx
#
29.03.2016548.84 Кб833УИП_краткий курс_2013.docx
#
27.11.2019682.5 Кб7УМК ОЭ от 12.04 11г..doc
#
27.11.2019430.59 Кб8УМК по ОСиП.doc
#
25.11.201918.81 Mб91УП КП 20.12.11.doc