
ТЭЦ Лекции
.pdf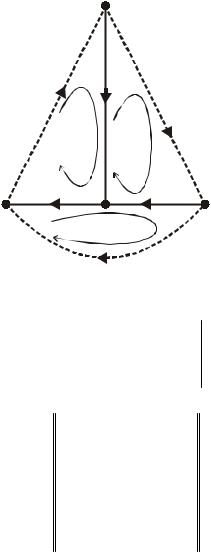
21 /102
|
|
2 |
|
|
|
I1в |
|
I5в |
|
|
|
|
|
I2в |
|
|
I1к |
I2к |
|
1 |
I4в |
|
3 |
|
4 |
I6в |
|||
|
|
I3к |
|
|
|
|
|
I3в |
|
Деревья графа показаны сплошными линиями, а ветви связи – пунктирными. Матрица соединения контурных сопротивлений B состоит из трёх строк и шести столбцов:
|
1 |
0 |
0 |
1 |
1 |
0 |
B = |
0 |
1 |
0 |
0 |
−1 |
1 |
|
0 |
0 |
1 |
−1 |
0 |
−1 |
|
|
|
|
|
|
|
Диагональная матрица сопротивлений
|
|
r1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
0 |
r2 |
0 |
0 |
0 |
0 |
|
rd |
= |
0 |
0 |
r3 |
0 |
0 |
0 |
|
0 |
0 |
0 |
r4 |
0 |
0 |
|||
|
|
0 0 0 0 r5 0
0 0 0 0 0 r6
Произведение матриц B и rd равно:
|
|
|
|
|
|
|
|
r1 |
0 |
0 |
|
|
|
|
r4 |
r5 |
0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Brd = |
0 r2 |
0 0 −r5 |
r6 |
. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
0 0 r3 |
−r4 |
0 −r6 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Квадратная матрица контурных сопротивлений определяется по формуле |
(4) |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
r(k ) = Br BT = |
|
r1 |
0 |
0 r4 |
r5 |
0 |
|
|
|
|
|
0 |
1 |
0 |
0 0 1 |
|
(r1 |
+ r4 + r5 ) |
−r5 |
|
) |
−r4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 r |
0 0 −r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
−r |
|
(r + r + r |
−r |
. |
|||||||||
d |
|
|
2 |
|
5 |
6 |
|
|
|
|
|
1 |
0 |
−1 |
|
|
|
5 |
2 |
5 |
6 |
|
6 |
|
||||||||||
|
|
0 0 r3 −r4 |
0 −r6 |
|
|
|
|
|
|
|
|
−r4 |
|
|
−r6 |
|
|
(r3 + r4 + r6 ) |
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
−1 |
0 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Матрица-столбец контурных токов I(k ) |
|
= |
|
|
I1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
I2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрица-столбец контурных ЭДС E(k ) |
|
|
|
|
|
|
E1 − E4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
|
|
−E |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E3 + E4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
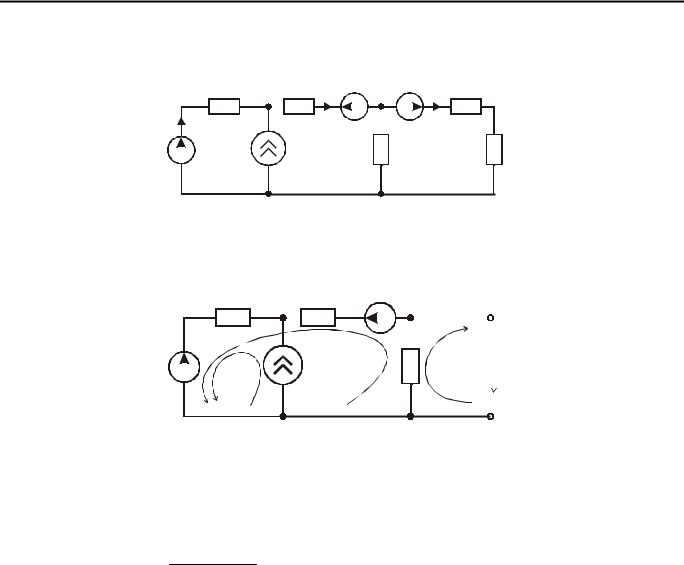
Пользуясь уравнением (3), матрицами r(k ) , I(k ) и E(ck ) , получим уравнения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
/102 |
|
(r1 + r4 + r5 ) I1 − r5 I2 − r4 I3 = E1 − E4 ; |
|
|||||||||||||||||||||
|
−r I + |
(r + r + r |
) I |
2 |
− r I |
3 |
= −E |
; |
|
||||||||||||||
|
5 |
1 |
|
2 |
6 |
5 |
|
6 |
|
2 |
|
|
|||||||||||
|
|
|
|
|
+ (r3 + r4 + r6 ) I3 = E3 + E4 . |
|
|||||||||||||||||
−r4 I1 − r6 I2 |
|
||||||||||||||||||||||
Матрица токов ветвей Iв легко определяется через матрицу контурных токов Ι(k ) по |
|
||||||||||||||||||||||
формуле |
|
|
|
|
|
Iв = BTI(k ) . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Для вышеприведённой схемы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1в |
|
|
|
|
|
1 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
I2в |
|
|
|
|
|
0 |
|
1 |
|
0 |
|
|
|
|
I1к |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
I3в |
|
= |
|
|
|
0 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
2к |
|
|
|
||||||
|
|
|
I4в |
|
|
|
|
|
1 |
|
0 |
|
−1 |
|
|
|
|
I |
|
|
|
|
|
|
|
|
I5в |
|
|
|
|
|
1 |
−1 |
|
0 |
|
|
|
|
3к |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
I6в |
|
|
|
|
|
0 |
|
1 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
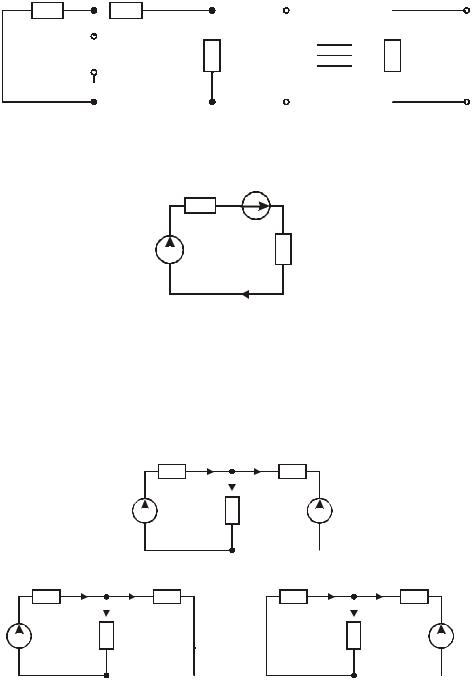
Из этого матричного уравнения сразу получаем равенства, определяющие токи ветвей через контурные токи:
I1в = I1к ; I2в = I2к ; I3в = I3к ; I4в = I1к − I3к ; I5в = I1к − I2к ; I6в = I2к − I3к .
Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С. В. Основы теории цепей. Учебник для вузов. Изд. 4-е, пер. М., «Энергия», 1975. 752 с. Стр. 52-55.
Метод эквивалентного генератора.
Данный метод основан на теореме об активном двухполюснике. Применение данного метода целесообразно для определения тока в какой-либо одной ветви сложной электрической цепи. Пусть дана схема в виде:
|
R1 |
|
R2 I |
E2 E3 I |
R3 |
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
J |
|
|
|
|
|
R4 |
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
E |
|
4 |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим ток I3 методом эквивалентного генератора. Этапы решения задачи.
1. Разрываем цепь в указанном нами участке. Находим Uxx по второму закону Кирхгофа, для этого рассматриваем контур I в следующей схеме:
|
R1 |
|
R2 |
E2 |
|
|
|
|
|
|
|
Iх |
|
J4 |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
|
J4 |
|
R4 |
|
U |
хх |
||||
|
|
|||||||||
|
|
|
|
|
||||||
|
|
|||||||||
|
|
|
|
|
||||||
E1 |
|
|
|
|
|
|
||||
Uxx + Ix R4 = 0,
Uxx = −Ix R4 .
2. Находим Ix по методу контурных токов, для этого рассматриваем контур с током Ix с учётом влияния источника тока J4 .
Ix (R1 + R2 + R4 ) + J4 R1 = E2 − E1 .
Откуда определяем Ix = E2 − E1 − J4 R1 .
R1 + R2 + R4
Соответственно напряжение холостого хода Uxx = Eист .
23 /102
3. Определяем сопротивление эквивалентного источника, которое должно быть равно внутреннему сопротивлению пассивизированной активной цепи. Ветви, где были включены источники тока, заменяются разрывом, а ветви с ЭДС – перемычкой. В зависимости от вида соединения сопротивлений составляем формулу для расчёта эквивалентного сопротивления,
которое равно сопротивлению на источнике Rэкв = Rист .
|
|
R = ( R1 + R2 ) R4 . |
||||
|
|
ист |
R1 + R2 |
+ R4 |
||
R1 |
|
R2 |
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
R4 |
|
|
Rист |
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Находим ток в нагрузке Iн = I3 . Строим эквивалентную схему замещения, учитывая то, что мы, |
||||||
разрывая цепь, исключили источник напряжения E3 |
и сопротивления R3 и R , следовательно, мы |
|||||
не учли их влияние на нашу цепь, поэтому в данной схеме мы должны включить их в цепь.
Rист E3
|
|
|
|
Eист |
Iн |
Rн |
|||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
|
= |
Eист + E3 |
|
|
|
|||
I |
|
, где R = R + R . |
|||||||
н |
Rист + Rн |
||||||||
|
|
|
|
н |
3 |
||||
|
|
|
|
|
|
|
|||
Метод наложения (суперпозиции).
Данный метод используется, когда действуют несколько источников напряжения и тока. При этом находят частичные токи (напряжения), а результирующие реакции определяются путём алгебраического суммирования частичных токов (напряжений).
Определить ток I3 |
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
1 |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
|
|
|
|
|
I3 |
|
|
|
|
E |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
R1 |
I’ |
|
I’ |
|
R2 |
|
|
|
|
|
|
|
|
|
R1 |
I’’ |
|
I’’ |
R2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
|
|
|
I3’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I3’’ |
|
|
|
|
E |
2 |
|
|
|
|||||
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
I ′ = I ′ |
|
R2 |
|
|
|
, где I ′ = |
|
|
E1 |
|
; I ′′ = I ′′ |
|
|
R1 |
|
|
, где I ′′ = |
|
E2 |
|
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
R2 R3 |
|
|
|
|
|
|
|
R1 R3 |
|
||||||||||||||||||||||||
3 1 R |
+ R |
1 |
|
R1 + |
3 2 |
R + R |
|
2 |
R2 + |
|
|
|
|||||||||||||||||||||||||||||
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
R2 + R3 |
|
|
|
|
|
|
|
|
|
|
|
|
R1 + R3 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Согласно принципу суперпозиции результирующий ток I |
3 |
определяется как: I |
3 |
= I |
′ |
+ I ′′ . |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
||||
Гармонические колебания. Основные понятия и определения.
Гармонические колебания – колебания, происходящие по закону синуса или косинуса. Графически гармоническое колебание можно представить в виде:

i(t) |
T |
|
Im |
||
|
||
ϕi |
t |
|
|
||
ω |
|
24 /102
u(t) |
T |
|
Um |
||
|
||
ϕu |
t |
|
|
||
ω |
|
где Im , |
Um – амплитуды тока и напряжения: максимальны по абсолютному значению; |
|
|
T = 1 f |
– период: промежуток времени, по истечении которого |
значения i (t ) |
или u (t ) |
повторяются; ω = 2 π f – угловая частота [рад/сек], f – циклическая частота [Гц]; |
|
||
ϕi , ϕu – |
начальные фазы тока и напряжения. |
|
|
Аналитически гармонический ток можно представить в виде: |
|
|
|
|
i (t ) = Im sin (ωt + ϕi ) = Im sin Ψi (t ) , либо i (t ) = Im cos (ωt + ϕi |
) = Im cos Ψi (t ) , |
(39) |
где Ψi (t ) = ωt + ϕi – текущая фаза тока. |
|
|
|
Аналогично для гармонического напряжения: |
|
|
|
|
u (t )=Um sin (ωt + ϕu )=Um sinΨu (t ) , либо u (t ) = Um cos (ωt + ϕu ) = Um cos Ψu (t ) , |
(40) |
|
где Ψu (t ) = ωt + ϕu |
– текущая фаза напряжения. Из соотношений (39) и (40) следует: ω = |
d Ψi, u |
. |
|
|||
|
|
dt |
|
Действующее (среднеквадратичное) значение гармонического тока и напряжения:
T
I = 1 ∫i2 (t ) dt , U = T 0
T
1 ∫u2 (t ) dt . (41)
T 0
Подставив (39) и (40) в (41), получим: I = |
I |
m |
|
, U = |
U |
m |
|
. |
(42) |
||||
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||
Среднее значение гармонического тока и напряжения: |
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
T |
1 |
T |
|
|
|
|
|||||
< I >= |
∫i (t ) dt , < U >= |
∫u (t ) dt . |
|
|
|
(43) |
|||||||
T |
T |
|
|
|
|||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Способы представления гармонических колебаний.
Гармонические колебания представляют в виде:
1.временных диаграмм;
2.векторных диаграмм;
3.комплексных чисел;
4.амплитудных и фазовых спектров;
Временное представление наглядно, но затруднительно при решении задач. Более удобно векторное представление, при котором каждому колебанию ставится в соответствие вращающийся вектор определённой длины с заданной начальной фазой.
Пусть имеем колебания токов: i1 (t ) = Im1 sin (ωt + ϕi1 ) и i2 (t ) = Im2 sin (ωt + ϕi2 ) . Определим
сумму этих токов: i3 (t ) = i1 (t ) + i2 (t ) = Im3 sin (ωt + ϕi3 ) , где Im3 = 
 Im12 + Im2 2 + 2 Im1 Im 2 cos (ϕi 2 − ϕi1 ) ,
Im12 + Im2 2 + 2 Im1 Im 2 cos (ϕi 2 − ϕi1 ) ,
ϕ = arctg Im1 sin ϕi1 + Im2 sin ϕi2 . |
||
i3 |
Im1 cos ϕi1 |
+ Im 2 cos ϕi2 |
|
||
Последние соотношения определяются из геометрии рисунка:
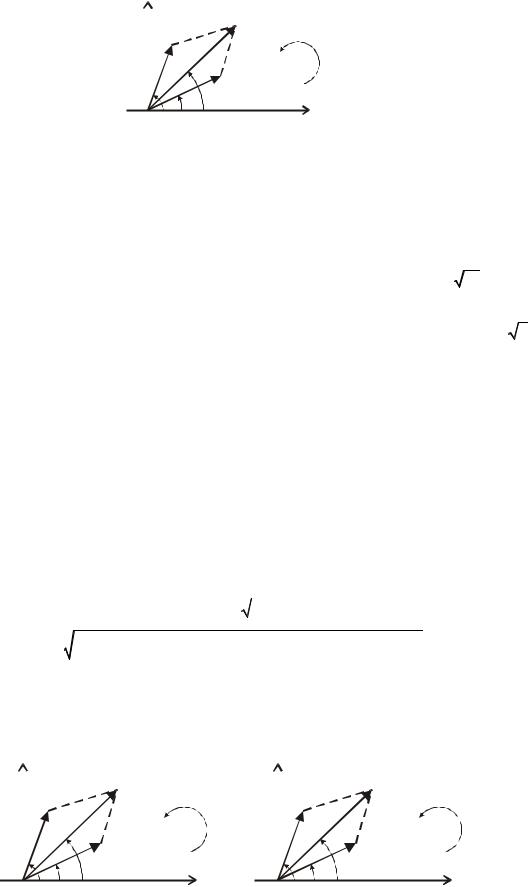
25 /102
|
b |
Im3 |
|
|
|
|
|
||
|
Im2 |
|
|
|
|
|
ω |
||
|
|
Im1 |
||
|
|
|
|
|
|
ϕi2ϕi1 |
ϕi3 |
|
a |
|
|
|
||
|
|
|
|
|
ϕi = ϕi 2 − ϕi1 – фазовый сдвиг между колебаниями токов i1 |
и i2 . |
|||
Векторной диаграммой называют совокупность векторов, изображающих гармонические колебания в электрической цепи. Векторные диаграммы строят для амплитудных или действующих значений.
Представления гармонических колебаний с помощью комплексных чисел лежат в основе символического метода расчёта электрических цепей (метод комплексных амплитуд).
|
i (t ) = I |
|
sin (ωt + ϕ ) → I |
|
= I |
|
ejji – комплексная амплитуда, где j = |
|
. |
|
|
|
|||
|
m |
m |
m |
−1 |
|||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|||
i (t ) = I |
m |
sin |
(ωt + ϕ ) |
→ I = I e j ji |
– |
комплексное действующее значение, причём I = |
I |
m |
. |
||||||
|
|
||||||||||||||
|
|
|
|
i |
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
I m = Im ejji , |
I = I e jji |
– запись в показательной форме. Существует запись в алгебраической |
|||||||||||||
форме, для этого используем формулу Эйлера: ej x = cos ( x) + jsin ( x) .
I m = Im cos (ϕi ) + j Im sin (ϕi ) = a + jb , где a = Im cos (ϕi ) , b = Im sin (ϕi )
Решим предыдущую задачу с помощью символического метода:
i (t ) = I |
m1 |
sin (ωt + ϕ |
) → I |
1 |
= I |
1 |
ejji1 |
= I cos (ϕ |
) + j I |
sin (ϕ |
i1 |
) , |
|||||||||||||||||||
1 |
|
|
i1 |
|
|
|
|
|
1 |
|
|
|
i1 |
|
|
1 |
|
|
|
||||||||||||
i (t ) = I |
m 2 |
sin (ωt + ϕ |
i2 |
) |
→ I |
2 |
= I |
2 |
ejji 2 |
= I |
2 |
cos (ϕ |
|
) + j I |
sin (ϕ |
|
) . |
||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
1 |
i2 |
|
||||||||||
Суммарный ток определяем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I 3 = I1 + I 2 |
= (I1 cos (ϕi1 ) + I2 cos (ϕi2 )) + j(I1 sin (ϕi1 ) + I2 sin (ϕi 2 )) . |
||||||||||||||||||||||||||||||
Последнее выражение |
представлено |
|
в алгебраической |
форме, |
его необходимо перевести |
||||||||||||||||||||||||||
в показательную, используя соотношение: a + jb = |
|
|
|
|
|
|
|
ej×arctg |
b |
|
|
|
|
|
|
|
|||||||||||||||
|
a2 |
+ b2 |
|
|
. Таким образом: I 3 = I3 e jji3 . |
||||||||||||||||||||||||||
|
|
a |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
I3 = |
|
|
(I1 cos (ϕi1 ) + I2 cos (ϕi 2 ))2 + (I1 sin (ϕi1 ) + I2 sin (ϕi2 ))2 |
, |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
ϕ |
= arctg |
I1 sin ϕi1 + I2 sin ϕi 2 |
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
i3 |
|
|
|
I1 cos ϕi1 + I2 cos ϕi2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Полученные комплексы токов удобно представить в виде векторной диаграммы на |
|||||||||||||||||||||||||||||||
комплексной плоскости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
I3 |
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
Im3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
I2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|||||||||
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
ϕi3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕi3 |
|
|
|
|
|||
|
ϕi2ϕi1 |
|
|
|
Re |
|
|
|
|
|
|
|
ϕi2ϕi1 |
|
|
|
|
|
Re |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Гармонические колебания в резистивных, индуктивных и ёмкостных элементах.
Пусть к резистивному элементу приложено гармоническое напряжение:
u (t ) = Um sin (ωt + ϕu ) . |
(44) |
Согласно закону Ома через резистор протекает гармонический ток:
26 /102
|
|
|
|
|
|
|
|
|
i (t ) = |
u (t ) |
|
= |
Um |
sin (ωt + ϕu ) = Im sin (ωt + ϕi ) . |
|||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(45) |
|
|
|
|
|
|
|
|
|
|
|
|
|
i(t) |
|
|
|
|
|
|
|
|
|
b |
Um |
|
b |
U |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
I |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
u(t) |
|
R |
|
|
|
|
|
|
|
ϕi=ϕu |
|
|
ϕi=ϕu |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
a 0 |
|
|
a |
||||||
|
|
|
Um |
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из (45) I |
m |
= |
и I = |
, ϕ |
u |
= ϕ – начальные фазы напряжения и тока равны! |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
R |
|
|
|
R |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Введём понятие фазового сдвига между входным напряжением и током, протекающим в цепи:
|
|
|
|
ϕ = ϕu − ϕi . |
|
|
|
|
|
|
|
(46) |
||
Вывод: в резистивном элементе фазовый сдвиг между напряжением и током равен нулю! |
|
|||||||||||||
Пусть в индуктивном элементе протекает ток: i (t ) = Im sin (ωt + ϕi ) . |
|
|
|
|
||||||||||
Учитывая связь между током и напряжением на индуктивности, получаем: |
|
|
|
|||||||||||
u (t ) = L |
d i |
= I |
|
ω L cos (ωt + ϕ ) = I |
|
ω L sin |
|
ωt + ϕ + |
π = U |
|
sin (ωt + ϕ |
|
) . |
(47) |
|
m |
m |
|
m |
u |
|||||||||
|
d t |
i |
|
i |
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
Из (47) |
Um = Im ω L = Im X L и U = I ω L = I X L , где |
X L = ω L – сопротивление на индуктивности, |
||||||
B = |
1 |
= |
1 |
– проводимость на индуктивности; ϕ |
|
= ϕ + π |
, откуда фазовый сдвиг определяется |
|
|
ωL |
u |
||||||
L |
X L |
|
|
i |
2 |
|
||
|
|
|
|
|
|
|||
как: ϕ = ϕu − ϕi = π . 2
Вывод: в индуктивности фазовый сдвиг между напряжением и током равен 90° !
i(t) |
Um |
b |
|
|
b |
ϕ |
|
U |
ϕ |
||
u(t) |
|
Im |
|
ϕu |
I |
L |
ϕu |
|
|
||
|
ϕi |
|
|
ϕi |
|
|
|
|
|
||
|
|
0 |
a |
0 |
a |
Пусть напряжение вида (44) приложено к ёмкостному элементу, тогда |
|||||
|
|
|
|
|
|
|
i (t ) = C |
d u |
= U |
|
C ωcos (ωt + ϕ |
) = U |
|
C ωsin |
|
ωt + ϕ |
|
+ |
π |
= I |
|
sin (ωt + ϕ ) . |
(48) |
||||
|
|
|
|
|
|
|
m |
m |
|
u |
|
m |
|||||||||||||||
|
|
|
|
|
|
|
|
|
d t |
|
u |
|
|
|
|
|
|
|
i |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
Из |
(48) |
Im = Um ωC = Um BC и |
I = U ωC = U BC , |
|
где |
|
BC = ωC |
– |
проводимость на |
ёмкости, |
|||||||||||||||||
X |
|
= |
1 |
= |
1 |
– сопротивление на ёмкости; ϕ = ϕ |
|
+ π , откуда фазовый сдвиг определяется как: |
|||||||||||||||||||
C |
|
ωC |
u |
||||||||||||||||||||||||
|
|
|
BC |
|
|
|
|
|
|
|
i |
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ϕ = ϕ |
u |
− ϕ = − π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
i |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: в ёмкости фазовый сдвиг между напряжением и током равен –90 ° !
27 /102
|
|
|
|
|
|
i(t) |
|
|
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
Im |
|
|
|
|
|
|
|
I |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕi |
|
|
|
|
|
|
|
|
ϕi |
|
|
|
|
|
|
|
|
u(t) |
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
ϕ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕu |
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
U |
|
|
|
0 |
|
|
|
ϕu |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
U |
|
|
|
||
Гармонические колебания в цепи при последовательном соединении R, L, C |
||||||||||||||||||||||||||
элементов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть в последовательной RLC-цепи протекает ток i (t ) = Im sin (ωt + ϕi ) . Согласно II закону |
|||||||||||||||||||||||||
Кирхгофа u (t ) = uR (t ) + uL (t ) + uC |
(t ) = i (t ) R + L d i + 1 |
∫ |
i (t ) d t . Подставим ток в явном виде: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d t |
C |
|
|
|
|
|
|
|
|
|
|
||
|
|
u (t ) = I |
m |
R sin (ωt + ϕ ) + I |
m |
ω L sin |
ωt + ϕ |
+ π |
+ I |
m |
1 |
|
sin ωt + ϕ |
u |
− |
π . |
||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
|
ωC |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|||
Запишем выражение в более компактном виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
u (t ) = UmR sin (ωt + ϕR ) + UmL sin (ωt + ϕL ) + UmC sin (ωt + ϕC ) , где |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
UmR = Im R , UmL = Im ω L = Im X L , UmC = Im ωC |
= Im X C , |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
ϕ |
uR |
= ϕ , ϕ |
uL |
= ϕ + π , ϕ |
uC |
= ϕ − π . |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
i |
2 |
|
|
i |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
uR(t) |
|
i(t) |
|
|
|
|
|
b |
|
Um |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ump |
|
|
|
|||||
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕu |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
u(t) |
|
|
L uL(t) |
|
|
|
|
|
|
UmR |
|
|
|
|||||||
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
ϕi |
|
Im |
|
|
|
|
|
|||
|
|
|
|
|
|
uC(t) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
a |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ump = UmL −UmC = Im ( X L − X C ) = Im X – |
реактивная составляющая напряжения, |
|
|
|||||||||||||||||||||||
X = X L − X C |
= ω L − |
1 |
– реактивное сопротивление. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z = |
R2 + X 2 |
= |
R2 + ( X L − X C ) |
2 |
= |
|
|
|
|
|
1 |
2 |
– |
полное сопротивление цепи. |
||||||||||||
|
R2 + ω L − |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
Для удобного анализа последовательной RLC-цепи используют треугольник сопротивлений.
Z
 ϕ X
ϕ X
R
|
|
|
X L − X C |
|
ω L − |
1 |
|
|
ϕ = arctg |
X |
= arctg |
= arctg |
ωC |
. |
|||
|
||||||||
R |
|
R |
|
|||||
|
|
R |
|
|
||||
ϕ > 0 – индуктивный характер цепи.
28 /102
ϕ< 0 – ёмкостный характер цепи.
ϕ= 0 – резонанс напряжений.
При резонансе напряжений полное сопротивление последовательной RLC-цепи равно резистивному! Определим частоту, на которой происходит явление резонанса из условия:
ω0 L − |
1 |
= 0 , откуда ω0 |
= |
|
1 |
|
[рад/c], |
f0 = |
|
1 |
|
[Гц]. |
|
ω0 C |
|
|
|
2 π |
|
|
|
||||||
|
|
||||||||||||
|
|
|
|
L C |
|
|
L C |
||||||
Резонанс – это явление, когда фазовый сдвиг между входным напряжением и током равен нулю!
Гармонические колебания в цепи при параллельном соединении R, L, C элементов.
i(t) |
|
|
|
|
|
|
|
|
iG(t |
) |
iL(t) |
|
|
iC(t) |
|
|
|
||||||
u(t) |
|
||||||
G |
L |
|
|
|
C |
||
|
|
|
|||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно I закону Кирхгофа: i (t ) = iG (t ) + iL (t ) + iC (t ) Напряжение на входе цепи: u (t ) = Um sin (ωt + ϕu )
Поскольку: i (t ) = G u (t ) + C |
d u |
+ |
1 |
∫u (t ) dt , то после подстановки имеем: |
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d t |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i (t ) = GUm sin (ωt + ϕu ) + ωC Um sin |
|
|
|
|
|
|
π |
|
|
|
1 |
|
|
|
|
|
|
|
|
π |
|
|||||||||
ωt + ϕu + |
|
|
+ |
|
|
|
|
|
Um sin |
ωt + ϕu |
− |
2 |
. |
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
ω L |
|
|
|
|
|
|
|
|
|||||||
Введём обозначения: I |
= GU |
|
, I |
|
= ωC U |
|
|
= B U |
|
|
, I |
= |
1 |
U |
|
= B U |
, |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
mG |
|
|
|
m |
|
mC |
|
|
|
|
m |
|
C |
|
|
m |
mL |
|
ω L |
m |
|
|
L |
m |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ϕ = ϕ |
u |
, ϕ = ϕ |
u |
+ π , ϕ = ϕ |
u |
− π . |
|
|
|
|
|
|
|
|
||||||||||||||||
iG |
|
|
|
iC |
|
2 |
|
|
iL |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Треугольник проводимостей
b |
Im |
|
Um |
|
|
Imp |
|||
|
|
|||
ϕu |
ϕ<0 |
|
Y |
|
ImG |
ϕ<0 B |
|||
|
||||
0 |
|
a |
G |
|
|
|
Imp = ImC − ImL = ( BC − BL )Um = BUm – реактивная составляющая тока.
B = B − B = ωC − |
1 |
|
|
реактивная проводимость. Y = |
|
|
|
|
|
|
|||||||||||
– |
G2 + B2 |
– полная проводимость. |
|||||||||||||||||||
ω L |
|||||||||||||||||||||
C L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ωC − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ = −arctg |
B |
= −arctg |
ω L |
– фазовый сдвиг между входным напряжением и током цепи. |
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
G |
||||||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При ϕ = 0 наступает резонанс токов Y = G . Определим резонансную частоту из условия: |
|||||||||||||||||||||
|
|
ω0 C − |
1 |
|
= 0 , отсюда ω0 = |
|
1 |
|
[рад/c], f0 = |
1 |
|
[Гц]. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
ω0 L |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
L C |
2 π L C |
|||||||||||

29 /102
Закон Ома в комплексной форме для элементов R, L и C.
Символический метод расчёта (СМР) позволяет тригонометрические и геометрические операции свести к алгебраическим операциям над комплексными числами. Это упрощает расчёт.
i (t ) = Im ej(ωt +ϕi ) = Im ejϕi ejωt = I m ejωt , u (t ) = Um ej(ωt +ϕu ) = Um ejϕu ejωt = |
U |
m ejωt . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
где I m = Im ejϕi |
, U m = Um ejϕu |
|
|
– |
|
комплексные амплитуды тока и напряжения. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
I = |
|
Im |
|
e |
jϕi |
, U = |
Um |
e |
jϕu |
– комплексные действующие значения тока и напряжения. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Запишем закон Ома в комплексной форме для элементов R, L и C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Для резистивного элемента: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
u (t ) = R ×i (t ) |
или i (t ) = G ×u (t ) , то U m = R × I m , I m = G ×U m или U = R × I , |
I = G × |
U |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Для индуктивного элемента: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u (t ) = L |
d i |
= jw L I m |
ejωt или i (t ) = |
1 |
|
|
u (t ) dt = |
|
|
1 |
|
U m ejωt . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L ∫ |
jw L |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
U m = jw L I m = Z L I m , |
|
I m |
= |
|
1 |
|
U m = Y L U m , или U = jw L I = Z L I , |
I = |
|
|
1 |
|
|
U |
= Y L U . |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jw L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jw L |
|||||||||||
Z L = jw L – |
|
комплексное сопротивление индуктивности (алгебраическая форма). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= w L ej |
π |
|
= X L ej |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Z L |
2 |
|
|
2 |
– |
комплексное сопротивление индуктивности (показательная форма). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Y L |
= |
1 |
|
|
|
– |
|
комплексная проводимость индуктивности (алгебраическая форма). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
jw L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Y |
= |
|
e− j |
2 = B e− j 2 |
– |
|
|
комплексная проводимость индуктивности (показательная форма). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L |
|
w L |
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из последних соотношений видно: |
|
|
Z L |
|
= X L , |
|
Y L |
|
= BL . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
3. Для ёмкостного элемента: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d u |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i (t ) |
= C |
|
|
|
= jwC U m |
ejωt или u (t ) = |
|
|
∫i (t ) dt = |
|
|
|
I m ejωt . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d t |
|
C |
|
j wC |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, U |
|
= |
|
|
1 |
|
|
|
|
I |
|
|
= Z |
|
|
I |
|
, или I = jwC U = Y |
|
U , U = |
1 |
|
|
|
I = Z |
|
I . |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
m |
C |
m |
C |
|
|
|
|
|
C |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Y C = jwC – |
|
|
|
|
|
|
|
|
|
|
jwC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jwC |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
комплексная проводимость на ёмкости (алгебраическая форма). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Y C
Z C
Z C
= wC ej |
π |
= B ej |
π |
|
|
||||
2 |
2 |
– |
комплексная проводимость ёмкости (показательная форма). |
||||||
|
|
|
|
|
C |
|
|
|
|
= |
1 |
|
|
– |
комплексное сопротивление ёмкости (алгебраическая форма). |
||||
jwC |
|||||||||
|
|
|
|
|
|
||||
|
1 |
e− j |
π |
|
− j |
π |
|||
= |
2 = X C e |
2 – комплексное сопротивление ёмкости (показательная форма). |
|||||||
|
|
||||||||
|
wC |
|
|
|
|
|
|||
Из последних соотношений видно: Z C = X C , Y C = BC .
Анализ последовательно соединенных RL, RC, RLC элементов символическим методом расчёта.
Анализ последовательной RL-цепи.
комплексная схема замещения
30 /102
|
R |
i(t) |
|
R |
|
I |
||
u(t) |
|
L |
U |
|
|
ZL |
||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании II закона Кирхгофа в комплексной форме:
U = U R + U L = R I + Z L I = (R + jω L) I = Z I , где Z – полное комплексное сопротивление цепи.
|
|
|
|
|
|
|
|
|
|
|
|
|
j×arctg wL |
|
|
|
|
|
|
|
|
Z = R + jω L = |
|
|
R2 + (ω L)2 |
|
e |
Z |
ejjz , где |
||||||
|
|
|
|
|
|
|
R = |
|
|||||||||
Z |
|
– модуль комплексного сопротивления, ϕz |
– |
аргумент комплексного сопротивления. |
|||||||||||||
|
|||||||||||||||||
ϕ = ϕz |
= arctg ω L = arctg |
X L |
– фазовый сдвиг между входным напряжением и током. |
||||||||||||||
|
|||||||||||||||||
|
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
U |
UL |
||||||
|
|
|
|
|
|
|
|
|
|
ϕ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
I Re |
|||||
|
|
|
|
|
0 |
|
|
UR |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из диаграммы видно, что фазовый сдвиг между напряжением и током больше нуля. Вывод: цепь носит индуктивный характер
Анализ последовательной RС-цепи.
комплексная схема замещения
|
|
|
|
|
|
|
R |
i(t) |
|
|
|
|
|
R |
|
I |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
u(t) |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
ZC |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании II закона Кирхгофа в комплексной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
2 |
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- j×arctg |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
U = |
U |
R + U C = R I + Z C |
I = R + |
|
|
|
|
|
|
I |
= Z I , где Z = R − j |
|
|
|
= |
|
R2 + |
|
|
|
e |
|
R wC = |
Z |
ejjz . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
jωC |
|
|
|
ωC |
|
|
|
ωC |
|
|
|
|
|
|
|
|||||||||||
ϕ = ϕz = −arctg |
|
= −arctg |
X C |
– |
фазовый сдвиг между входным напряжением и током. |
||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
R ωC |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
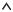 Im UR I Re
Im UR I Re
0 ϕ
UC
U
Из диаграммы видно, что фазовый сдвиг между напряжением и током меньше нуля. Вывод: цепь носит ёмкостный характер
Анализ последовательной RLС-цепи.
комплексная схема замещения
