ДИФУР ГУРЕВИЧ ЛЕКЦИИ

Учитывая (7.29), заключаем, что k~ k ! ! 1, а поэтому из

Y (x) 0 ïðè x

теоремы 7.6 следует, что возмущенная система асимптотически устойчи- ва.

7.5.Метод Ляпунова

Рассмотрим систему дифференциальных уравнений

Как было показано в теореме 7.3, вопрос об устойчивости произвольного решения может быть сведен к исследованию устойчивости тривиального решения некоторой приведенной системы. Поэтому, не теряя общности, можно считать, что система (7.32) является приведенной, т. е. F (x; 0)

0.

Обозначим через Qb множество f(x; Y ) j x a; kY k < bg, где b > 0. Определение 7.9. Непрерывная скалярная функция v(x; Y ) назы-

вается знакоположительной(знакоотрицательной) в Qb, åñëè äëÿ ëþ- áûõ (x; Y ) 2 Qb выполняется неравенство v(x; Y ) 0 (v(x; Y ) 0).

Определение 7.10. Непрерывная скалярная функция v(x; Y ) на-

зывается положительно определенной в Qb, если существует функция w(Y ), непрерывная в области kY k < b, такая что v(x; Y ) w(Y ) > 0

ïðè Y 6= 0 è v(x; 0) = w(0) = 0.

Пример 7.4. Пусть n = 2. Рассмотрим v(x; Y ) = v(x; y1; y2) = = y12 +y22 2 y1y2 cos x. Убедимся, что при j j < 1 эта функция является положительно определенной. В самом деле,

v(x; y1; y2) y12+y22 2j jjy1jjy2j y12+y22 j j(y12+y22) = (1 j j)(y12+y22);

и, следовательно, в качестве w(y1; y2) можно взять (1 j j)(y12 +y22). При= 1 функция v(x; y1; y2) является знакоположительной.

Предположим теперь, что функция v(x; Y ) имеет непрерывные частные производные по всем переменным в области Qb.

141

Определение 7.11. Производной v(x; Y ) в силу системы (7.32) на-

Теорема Ляпунова. Если для системы (7.32) существует положительно определенная функция v(x; Y ), имеющая в Qb непрерывные

частные производные по всем переменным, причем ее производная в силу системы знакоотрицательна, то тривиальное решение системы (7.32) устойчиво.

Доказательство. Из условий теоремы следует, что существует непрерывная функция w(Y ), такая что

v(x; Y ) w(Y ) > 0 ïðè Y 6= 0; v(x; 0) = w(0) = 0:

Возьмем произвольное " > 0 и в пространстве Rn рассмотрим сферу

S" = fY j kY k = "g:

Òàê êàê S" ограниченное замкнутое множество, то функция w(Y ) достигает на ней минимальное значение, которое положительно. Обозна- чим его через . Далее, так как функция v(a; Y ) непрерывна по Y , при-

чем v(a; 0) = 0, то существует шар = fY j kY k g, < ", такой что при Y 2 выполняется неравенство 0 v(a; Y ) < .

Рассмотрим произвольное нетривиальное решение ~

Y (x), удовлетво-

ряющее условию k~ k

Y (a) < . Докажем, что траектория этого решения

, ò. å. k~ k

находится в S" Y (x) < " при любых x a. В самом деле, предпо-

, в которой k~ k

ложим противное: существует точка x1 Y (x1) = ". Предпо-

первая такая точка, т. е. k~ k

ложим дополнительно, что x1 Y (x) < " ïðè a x < x1. Обозначим v~(x) = v(x; y~1(x); : : : ; y~n(x)). Подсчитаем производную v(x) по x по правилу дифференцирования сложной функции:

n

+ X @v(x; y~1(x); : : : ; y~n(x)))fk(x; y~1(x); : : : ; y~n(x)): @yk

k=1

Отсюда из знакоотрицательности производной в силу системы прихо- дим к выводу, что dv~dx(x) 0. Следовательно, функция v~(x) невозрас-

142

Замечание. Использованная при доказательстве теоремы функция v(x; Y ) называется функцией Ляпунова.

Теперь приведем пример теоремы, в которой с помощью функции Ляпунова устанавливается неустойчивость тривиального решения приведенной системы (7.32).

Теорема Четаева. Пусть для некоторого положительного h (h < < b) существует функция v(x; Y ), которая обладает следующими свойствами:

1) непрерывно дифференцируема на множестве Q = f(x; Y ) j x

a; kY k hg;

2)v(a; O) = 0, и в любой окрестности точки (a; O) существует точ- ка (a; Y0), в которой v(a; Y0) > 0;

3)на множестве Q функция v(x; Y ) ограничена сверху;

4) для любого > 0 существует > 0, такое что если v(x; Y ) ,

то для производной в силу системы (7.32) справедливо неравенство

dv(x;Y (x)) , dx

тогда тривиальное решение системы (7.32) неустойчиво. Доказательство. Пусть произвольно малое положительное чис-

ло ( < h). Докажем, что существует решение Y (x) системы (7.32), которое удовлетворяет следующим условиям: а) kY (a)k < ; б) для некоторого x1 > a выполняется kY (x1)k = h. Отсюда будет следовать утверждение теоремы. В силу условия 2) существует точка (a; Y0), такая что kY0k < è v(a; Y0) = > 0. В качестве Y (x) возьмем решение задачи Коши с начальным условием Y (a) = Y0. Предположим, что kY (x)k < h для всех x a. Рассмотрим функцию '(x) = v(x; Y (x)), которая имеет непрерывную производную при x a в силу 1). Так как '(a) = , то '0(a) > 0, где соответствует из условия 4). Убедимся, что '0(x) > 0 для любых x a. В самом деле, предположим противное,

т. е. что существует x0, такое что '0(x0) = 0. Не теряя общности, можно считать, что '0(x) > 0 ïðè x 2 [a; x0). Отсюда следует, что на отрезке

[a; x0] функция '(x) является возрастающей и потому '(x0) , но тогда '0(x0) > 0. Получили противоречие. Следовательно, '0(x) > 0,

поэтому '(x) для всех x a. Но тогда для таких x имеет место '0(x) . Интегрируя последнее неравенство по отрезку [a; x], получаем '(x) '(a) + (x a) ! 1 при x ! 1. Отсюда следует неограниченность сверху функции '(x), что противоречит условию 3).

Подобные теоремы имеют место и для случая асимптотической устой- чивости (неустойчивости).

143

В заключение этого раздела приведем без доказательства теорему об устойчивости "по первому приближению" , в которой изучается вопрос об устойчивости возмущенной системы (вообще говоря, нелинейной).

Теорема 7.11. Рассмотрим систему

Y 0 = AY + F (x; Y );

где A постоянная матрица, F (x; Y ) вектор-функция.

Пусть при x a и kY k h функция F (x; Y ) имеет непрерывные частные производные и kF (x; Y )k (Y )kY k, где (Y ) ! 0 при Y ! 0, тогда:

1)если все собственные значения матрицы A имеют отрицательные

вещественные части, то нулевое решение данной системы асимптотически устойчиво;

2)если матрица A имеет собственное значение с положительной вещественной частью, то нулевое решение неустойчиво;

3) в случае, когда max Re j = 0, наличие устойчивости или неустой-

j

чивости зависит не только от матрицы A, но и от функции

F (x; Y ).

144

8. Особые точки дифференциальных уравнений

Рассмотрим дифференциальное уравнение

где вещественные функции f и g определены и непрерывны вместе с частными производными fx, fy, gx, gy в области D R2.

Определение. Точка (x0; y0) 2 D называется особой точкой уравнения (8.1), если

f(x0; y0) = g(x0; y0) = 0:

В этом разделе будет изучено качественное поведение решений уравнения (8.1) в окрестности изолированной особой точки.

Пусть (x0; y0) особая точка уравнения (8.1). Не уменьшая общности, будем считать, что

(x0; y0) = (0; 0):

Преобразуем правую часть уравнения по формуле Тейлора:

f(x; y) = ax + by + r1(x; y); g(x; y) cx + dy + r2(x; y)

ãäå a = fx(0; 0); b = fy(0; 0); c = gx(0; 0); d = gy(0; 0); r1; r2

малые по сравнению с jxj + jyj.

В силу малости величин r1 è r2 естественно ожидать, что в достаточ- но малой окрестности точки (0; 0) поведение решений уравнения (8.1) похоже на поведение решений уравнения

Доказательство этого факта довольно трудоемко, и мы его не приводим. Итак, будем исследовать поведение решений уравнения (8.2) при условии (8.3) в окрестности особой точки (0; 0). Уравнение (8.3) явля-

ется однородным, и его решение можно найти в явном виде. Но мы воспользуемся другим методом, более наглядным с геометрической точки зрения.

145

8.1.Интегральные кривые и фазовые траектории

Уравнение (8.2) тесно связано со следующей системой дифференциальных уравнений:

x(t) = cx(t) + dy(t);

Определение. Пусть x(t); y(t) некоторое решение системы (8.4). Множество точек f(x(t); y(t))jt Rg 2 R2 называется фазовой траекто-

рией (фазовой кривой) системы (8.4).

Замечание. Точка (0; 0) является фазовой траекторией нулевого ре-

шения это так называемая точка равновесия системы (8.4). Других то- чек равновесия в силу (8.3) нет, и все остальные фазовые кривые через (0; 0) не проходят.

Теорема 8.1. Ненулевые фазовые траектории системы (8.4) являются интегральными кривыми уравнения (8.2). Обратно, если функция y = '(x); x0 6 x 6 x1; является решением уравнения (8.2), то соответствующая интегральная кривая f(x; '(x))jx0 6 x 6 x1g является участком некоторой ненулевой фазовой траектории системы (8.4).

Доказательство. Пусть ненулевая фазовая кривая (x(t); y(t)) проходит через точку (x0; y0), ò.å. x(t0) = x0; y(t0) = y0: Обозначим через угол наклона касательной к этой кривой в точке (x0; y0). Тогда

Отсюда следует, что совпадает со значением поля направления уравне-

ния (8.2) в точке (x0; y0). Предполагается, конечно, что если cx0+dy0 = 0, то поле направлений в этой точке вертикально. Таким образом, в каждой своей точке фазовая кривая (x(t); y(t)) касается поля направлений

уравнения (8.2), т.е. является интегральной кривой этого уравнения. Пусть теперь функция y = '(x); x0 6 x 6 x1; является некоторым

решением уравнения (8.2). По определению решения выполняется тождество

причем знаменатель нигде не обращается в 0. Предположим, для опре-

деленности, что

cx + d'(x) > 0

(случай cx + d'(x) < 0 рассматривается аналогично). Определим на

146

[x0; x1] монотонно возрастающую функцию t(x) по формуле

[0; t1]; t1 = t(x1): Положим также y(t) = '(x(t)): Используя правила

дифференцирования сложных и обратных функций и тождество (8.5), имеем:

участком фазовой траектории системы (8.4). С другой стороны,

y = '(x): Теорема доказана.

Таким образом, теорема 8.1 сводит изучение поведения решений уравнения (8.1) в окрестности изолированной особой точки к изучению поведения фазовых траекторий системы (8.4) в окрестности нуля при условии (8.3).

Запишем систему (8.4) в векторной форме:

147

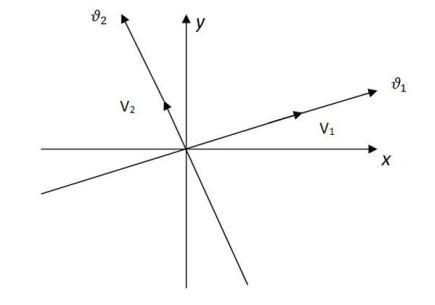
5.1 кратный корень уравнения (8.7), которому соответствуют два линейно независимых собственных вектора матрицы A;

6.1 кратный корень уравнения (8.7), которому соответствует только один (с точностью до множителя) собственный вектор.

Âкаждом из этих случаев поведение фазовых траекторий будет различ- ным. Рассмотрим подробно эти случаи по порядку.

8.2.Óçåë

Предположим, что 2 < 1 < 0 (случай 0 < 1 < 2 рассматривается аналогично и дает то же поведение фазовых траекторий).

Пусть Vj нормированный собственный вектор, соответствующий собственному значению j(j = 1; 2) матрицы A. Как известно (см. раздел 6), любое решение системы (8.6) имеет вид

ãäå c1; c2 некоторые числа.

Предположим сначала, что векторы V1 è V2 ортогональны: Перейдем в плоскости x0y к новой системе координат v10v2, îñè êî-

торой направлены вдоль V1 è V2.

Ðèñ. 8.1

Соотношения (8.8) в координатной форме примут вид

Соотношения (8.9) представляют собой параметрические уравнения фазовых траекторий.

148

Åñëè c2 = 0 è c1 > 0, то при t 2 R получаем положительную часть оси v1, à åñëè c1 < 0, то фазовой траекторией будет отрицательная часть оси v1.

Åñëè c1 = 0 è c2 > 0, то фазовой тракторией будет положительная часть оси v2, à ïðè c2 < 0 отрицательная часть оси v2.

Пусть теперь c1 c2 6= 0. Для определенности предположим, что c1 > 0; c2 > 0. В этом случае из соотношений (8.9) легко исключить параметр t и получить уравнение фазовой траектории

c2 2

v2 = ec1 v1 1 ; v1 > 0:

Аналогично рассматриваются случаи, когда c1 è c2 имеют другие знаки.

В результате получаем, что все ненулевые фазовые траектории (при всевозможных c1 è c2, c1 c2 6= 0) можно задать формулой

где c произвольная ненулевая константа. Фазовые траектории представлены на рис. 8.2.

Замечание. Если 2 = 2, то фазовыми траекториями будут парабо-

лы и полуоси.

1

В общем случае векторы V1 è V2 образуют неортогональный базис. Ïðè ýòîì îñè v1 è v2 не ортогональны (см. рис. 8.3).

Ðèñ. 8.2

Ðèñ. 8.3

Таким образом, в рассматриваемом случае качественное поведение фазовых траекторий имеет вид

149

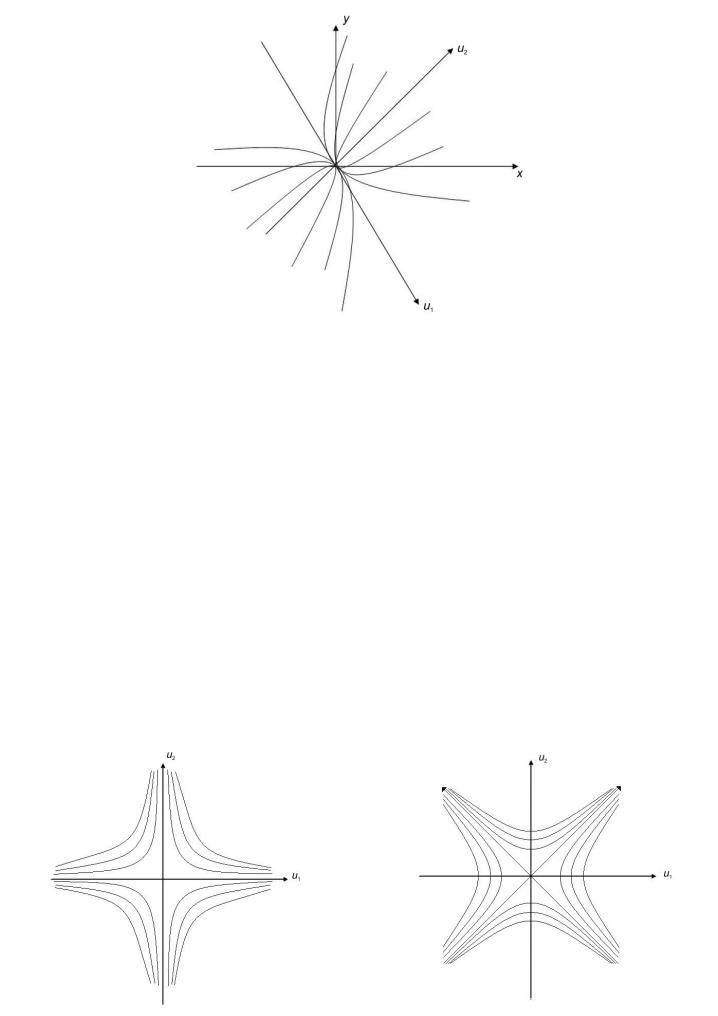
Ðèñ. 8.4

Определение. Особая точка в рассмотренном случае называется узлом.

8.3.Седло

Предположим, что корни 1 è 2 вещественные и имеют разные знаки. Рассуждая так же, как и в разделе 8.2, приходим к следующему результату. Если соответствующие собственные векторы V1 è V2 îð- тогональны, то положительные и отрицательные части координатных осей прямоугольной системы v10v2 будут фазовыми траекториями, а

все остальные ненулевые фазовые траектории определяются формулой (8.10). Из условия 2 < 0 следует, что в прямоугольной системе коорди-

1

íàò v10v2 фазовые траектории имеют вид, представленный на рис. 8.5.

150