ДИФУР ГУРЕВИЧ ЛЕКЦИИ

4.4.Теория Штурма

Âтеории Штурма исследуется колеблемость решений линейных уравнений.

Âкачестве объекта исследования ограничимся рассмотрением линейных однородных дифференциальных уравнений (4.3). В разделах 4.1 и

4.2было показано, что их можно преобразовать к виду, в котором нет первой производной. Поэтому будем изучать уравнения вида

где q(x) непрерывная функция.

Лемма 4.1. Пусть y0(x) нетривиальное решение уравнения (4.18)

è y0(x0) = 0, x0 2 (a; b). Тогда y00 (x0) 6= 0.

Доказательство. Пусть y00 (x0) = 0. В этом случае y(x) является

решением задачи Коши для уравнения (4.18) с начальными условиями y(x0) = 0, y0(x0) = 0. Задача Коши имеет единственное решение, кото-

рым, очевидно, является y0(x) 0, а это противоречит условию леммы.

Лемма 4.2. Пусть y0(x) нетривиальное решение уравнения (4.18). Тогда на любом отрезке [ ; ] (a; b) число нулей функции y0(x) конечно.

Доказательство. Предположим противное: y0(xk) = 0, k = 1; 2; : : :

è âñå xk 2 [ ; ]. По теореме Больцано-Вейерштрасса у этой последовательности нулей существует сходящаяся подпоследовательность. Не

уменьшая общности, предположим, что существует lim xk = x0. Î÷å-

k!1

видно, x0 2 [ ; ]. И поэтому y0(x0) = 0. Теперь рассмотрим

а этого не может быть по лемме 4.1. Лемма доказана.

Определение. Нетривиальное решение уравнения (4.18) называется колеблющимся на отрезке [ ; ], если оно обращается в ноль хотя бы в

двух точках этого отрезка.

Теорема 4.1.Если q(x) 0, то любое нетривиальное решение урав-

нения (4.18) имеет не более одного нуля, т. е. является неколеблющимся.

Доказательство. Пусть y(x) произвольное нетривиальное реше-

ние уравнения (4.18). Предположим, что x1, x2 нули y(x). В силу леммы 4.2 можно считать, что для всех x 2 (x1; x2) y(x) 6= 0, например y(x) > 0. Из леммы 4.1 следует, что в этом случае

81

С другой стороны, в рассматриваемом случае на отрезке [x1; x2] выпол-

няется неравенство

y00(x) = q(x)y(x) 0;

из которого следует, что функция y0(x) на этом отрезке не убывает, а это противоречит неравенству (4.19). Теорема доказана.

Теорема 4.2 (теорема Штурма). Пусть y1(x), y2(x) линейно независимые решения уравнения (4.18), x1 è x2 последовательные нули функции y1(x). Тогда в интервале (x1; x2) лежит ровно один ноль функции y2(x).

Доказательство. По формуле Остроградского Лиувилля для вронскиана W (x) функций y1(x) è y2(x) имеем

x

R

0dt

W (x) W (x1)e x1 = C;

причем C 6= 0, так как y1(x) è y2(x) линейно независимы. По определению вронскиана

W (xi) = y1(xi)y20 (xi) y10 (xi)y2(xi); i = 1; 2:

Между x1 è x2 нет других нулей функции y1(x), поэтому y10 (x1) è y10 (x2) имеют разные знаки, и в силу (4.20) y2(x1) è y2(x2) тоже имеют разные знаки. На основании этого делаем вывод, что существует x0 2 (x1; x2), в которой y2(x0) = 0.

Докажем, что x0 единственный ноль функции y2(x) на отрезке [x1; x2]. Если бы у функции y2(x) áûë åù¼ îäèí íîëü x0 2 (x1; x2), то по первой части доказательства между x0 è x0 лежал бы ещ¼ один ноль функции y1(x), а этого не может быть, так как x1, x2 последовательные нули функции y1(x). Теорема доказана.

Теорема 4.3 (теорема сравнения).Пусть y(x) ненулевое реше-

82

где a < x < b, q(x), Q(x) непрерывны и q(x) Q(x). Предположим,

÷òî x1, x2 два последовательных нуля функции y(x) и на отрезке [x1; x2] q(x) 6Q(x). Тогда существует x0 2 (x1; x2), в которой

z(x0) = 0.

Доказательство. Рассмотрим для определенности случай y(x) > 0, x1 < x < x2. Тогда в силу леммы 4.1 y0(x1) > 0 è y0(x2) < 0. Предположим, что z(x) 6= 0 на интервале (x1; x2), например z(x) > 0 (случай z(x) < 0 рассматривается аналогично).

По условию

y00(x) + q(x)y(x) 0; z00(x) + Q(x)z(x) 0:

Умножим первое тождество на z(x), второе на y(x) и вычтем из первого второе. В результате получим тождество

y00(x)z(x) z00(x)y(x) + (q(x) Q(x))y(x)z(x) 0;

которое можно записать в виде

dxd (y0(x)z(x) z0(x)y(x)) + (q(x) Q(x))y(x)z(x) 0:

Проинтегрировав обе части этого тождества от x1 äî x2, получим равен- ñòâî

x2

Z

y0(x2)z(x2) y0(x1)z(x1) + [q(t) Q(t)]y(t)z(t)dt = 0;

x1

àэтого не может быть, так как первые два слагаемых не положительны,

àинтеграл строго меньше нуля. Полученное противоречие доказывает

теорему.

Замечание. Если q(x) Q(x) на [x1; x2], то возможны два слу- чая. В первом случае y(x) и z(x) линейно зависимы на [x1; x2], и тогда x1; x2 последовательные нули z(x). Во втором случае y(x) и z(x) линейно независимые, и тогда по теореме Штурма существует x0 2 (x1; x2), в которой z(x0) = 0.

Теорема 4.4. Рассмотрим уравнение

83

Доказательство. Рассмотрим уравнение

z00 + Mz = 0:

p

Очевидно, z(x) = sin( M(x x1)) является решением этого уравнения. Имеем, что q(x) M и z(x1) = y(x1) = 0. Тогда по теореме сравнения и замечанию к ней следующий ноль z(x) не может лежать правее x2. Учитывая, что расстояние между любыми соседними нулями z(x) равно

p

M , можно сделать вывод, что

x2 x1 p : M

Таким образом, левая часть неравенства (4.25) доказана.

Правую часть неравенства (4.25) докажем от противного. Пусть стро- го между x1 è x2 можно вставить отрезок длины pm, т. е. предположим, ÷òî x2 x1 > pm. Для любого отрезка длины pm можно подобрать

решение уравнения u00 + mu = 0 так, что концы этого отрезка будут последовательными нулями этого решения. На этом отрезке решение y(x)

уравнения (4.23) с не меньшим чем m коэффициентом q(x) не имеет ну-

лей. Это противоречит теореме 4.3. Следовательно, отрезок длины p

m

вставить строго между x1 è x2 нельзя, т. е. x2 x1 pm. Теорема дока- çàíà.

Теперь, используя полученные результаты, выполним качественное исследование решений уравнения Бесселя

где положительный параметр, 6= 1; 2; : : :. В подразделе 3.6, приме-

нив метод обобщенных степенных рядов, мы нашли два линейно независимых решения уравнения Бесселя:

84

Формулы (4.27) позволяют выяснить поведение решений в окрестности x = 0, а именно:

Однако из формул (4.27) не видно, как ведут себя решения при x ! 1.

Займемся исследованием этого вопроса.

Преобразуем уравнение (4.26) к уравнению, не содержащему первую производную, с помощью замены

После такой замены уравнение (4.26) приводится к уравнению (4.7), которое в нашем случае имеет вид

По теореме 4.4 ( m = 1 ", M = 1 + ") при x > A расстояние h между соседними нулями любого нетривиального решения z(x) уравнения (4.29) удовлетворяет неравенству

Из формулы (4.28) следует, что нули y(x) совпадают с нулями z(x), по-

этому любое нетривиальное решение уравнения (4.26) имеет бесконеч- ное множество нулей, расстояние между которыми стремится к при

x ! 1.

Для полноты картины докажем еще одну лемму.

85

Лемма 4.3. Решения уравнения (4.29) ограничены при x ! 1.

Доказательство. Запишем уравнение в виде

Фундаментальной системой соответствующего однородного уравнения является система fsin x; cos xg, с помощью которой методом вариации

произвольных постоянных можно получить общее решение уравнения (4.33) в виде

ãäå C1, C2 произвольные постоянные.

Пусть теперь z(x) произвольное решение уравнения (4.32). Поло-

ãäå C = jC10j + jC20j. Отсюда, применяя неравенство Беллмана, получаем

Таким образом, любое решение уравнения (4.29) является ограниченным на [1; 1). Лемма доказана.

Из леммы 4.3 и формулы (4.28) следует, что любое решение уравнения Бесселя при x ! 1 стремится к 0.

Подводя итог нашего исследования, можно сказать, что качественная картинка (график) любого нетривиального решения уравнения Бесселя (4.29) имеет один из двух видов, представленных на рис. 4.1.

86

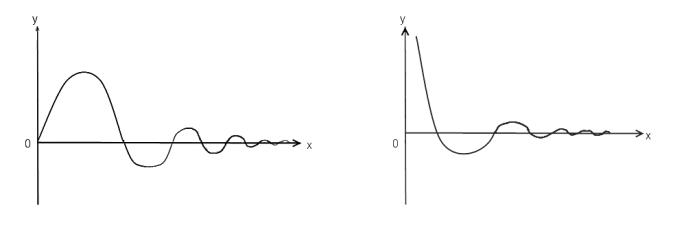
Ðèñ. 4.1

Около нуля знак решения может быть и отрицательным.

87

5.Краевые задачи

для дифференциальных уравнений второго порядка

5.1.Краевая задача и ее функция Грина

Рассмотрим уравнение

= 1; 2; : : : ; n; a j; b j; c ; k заданные числа, причем 0 k n 1,

ja k j + jb k j > 0; и, кроме того, как среди чисел a j, так и среди b j имеются отличные от нуля.

Определение 5.1. Условия вида (5.2) называются краевыми условиями .

Отметим, что в отличие от начальных условий задачи Коши краевые условия налагают определенные требования, связывающие значения искомого решения и его производных на концах отрезка [a; b].

Определение 5.2. Задача нахождения решения уравнения (5.1), удовлетворяющего краевым условиям (5.2), называется краевой задачей .

В отличие от задачи Коши краевая задача может не иметь решений, иметь единственное решение, иметь бесконечное множество решений. Иллюстрацией таких возможностей служат следующие краевые задачи:

В дальнейшем будем рассматривать лишь краевую задачу:

88

Наряду с (5.3) рассмотрим соответствующее однородное уравнение

Теорема 5.1. Предположим, что краевая задача (5.3)-(5.5) имеет решение. Тогда для того чтобы оно было единственным, необходимо и достаточно, чтобы однородная краевая задача (5.4)-(5.6) имела только тривиальное решение.

Доказательство. Необходимость. Воспользуемся методом от противного. Предположим, что краевая задача (5.4)-(5.6) имеет нетривиальное решение y0(x). Пусть, далее, y~(x) решение задачи (5.3)-(5.5). Но

тогда, очевидно, функция y0(x) + y~(x) является еще одним решением

этой задачи. Получили противоречие.

Достаточность. Пусть краевая задача (5.3)-(5.5) имеет два различ- ных решения y1(x) è y2(x). Но тогда функция y1(x) y2(x) является

нетривиальным решением (5.4)-(5.6), что противоречит предположению.

Изучим теперь вопрос о представлении решения краевой задачи (5.3)- (5.5) при условии что оно существует.

Определения 5.3. Функцией Грина краевой задачи (5.3)-(5.5) называется функция G(x; t), которая удовлетворяет следующим условиям:

1) G(x; t) непрерывна в квадрате a x; t b;

2)при любом фиксированном t 2 (a; b) функция G(x; t) имеет непрерывную производную по x в каждом из промежутков [a; t) и (t; b], причем последняя имеет при x = t скачок, равный единице, т. е.

@G(t + 0; t) @G(t 0; t) = 1; @x @x

3) в каждом из промежутков [a; t) и (t; b] функция G(x; t), рассматриваемая как функция x, удовлетворяет уравнению (5.6) и краевым усло-

âèÿì (5.4), (5.5).

Теорема 5.2. Если краевая задача (5.4)-(5.6) имеет только тривиальное решение, то функция Грина существует и единственна.

Доказательство. Пусть y1(x); y2(x) решения (5.6), удовлетворяющие начальным условиям y(a) = 0; y0(a) = 1 è y(b) = 0; y0(b) = 1 ñîîò-

ветственно. Прежде всего заметим, что эти функции образуют фундаментальную систему, то есть линейно независимы. В самом деле, предположим, что y1(x) = cy2(x), где c 6= 0. Но тогда, очевидно, функция y1(x)

89

удовлетворяет условиям (5.4), (5.5) и, следовательно, является нетривиальным решением краевой задачи (5.4)-(5.6), что противоречит предположению. Далее, из условия 3) следует, что должно иметь место представление

причем G(a; t) = G(b; t) = 0, то есть

(

a1(t)y1(a) + a2(t)y2(a) = 0; b1(t)y1(b) + b2(t)y2(b) = 0:

Учитывая начальные условия, приходим к выводу, что a2(t)y2(a) = 0; b1(t)y2(b) = 0. Íî ò.ê. y2(a) 6= 0; y1(b) 6= 0 (в противном случае решения y1(x) è y2(x) были бы линейно зависимы, т.к. их определитель Вронского при x = a или x = b имел бы нулевую строчку), то a2(t) 0; b1(t) 0 и, следовательно,

Из условия 1) теоремы следует, что функции a1(t); b2(t) должны быть непрерывными на [a; b], причем для любого t 2 [a; b] справедливо тож-

дество a1(t)y1(t) b2(t)y2(t). А из 2) имеем b2(t)y20 (t) a1(t)y10 (t) 1. Следовательно, эти функции должны удовлетворять системе

(

a1(t)y1(t) b2(t)y2(t) = 0; a1(t)y10 (t) b2(t)y20 (t) = 1:

Определителем этой системы является

а потому представим a1(t); b2(t) по формулам Крамера:

90