1. Система движется поступательно по отношению к системе.

 

Пусть в системе начало отсчета системы характеризуется радиус-вектором , а её скорость и ускорение – векторами и . Если положение точки в системе определяется радиус-вектором , а в системе – радиус-вектором , то ясно, что .

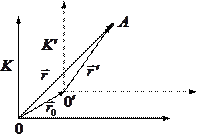 Пусть далее за промежуток времени точка 

совершит в системе элементарное перемещение .

Это перемещение складывается из перемещения вместе

с системой и перемещения относительно

системы, т.е.

. (1)

Поделив это выражение на , получим искомую формулу

преобразования скорости:

. (2)

Продифференцировав полученное выражение по времени, найдем и формулу преобразования ускорения:

. (3)

2. Система вращается с угловой скоростью вокруг оси, неподвижной в системе.

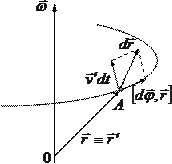 Получим сначала преобразования при условии .

Выберем начала отсчета и систем в произвольной точке 

на оси вращения. Тогда в обеих системах отсчета радиус-вектор точки

будет один и тот же: .

Если точка неподвижна в системе (), это значит, что

её перемещение в системе за время обусловлено только

поворотом радиус-вектора на угол вместе с системой

и равно векторному произведению .

Если точка движется относительно системы со скоростью ,

то за время она совершит дополнительное перемещение и тогда

. (4)

Поделив на , получим формулу преобразования скорости:

, (5)

где и - скорости точки в и системах соответственно.

Перейдем к ускорениям.

В соответствии с (5) в системе приращение вектора за время должно складываться из суммы приращений векторов и [, т.е.

, т.к. . (6)

 Если точка движется в системе с постоянной скоростью

(, то в системе это приращение обусловлено

только поворотом вектора вместе с системой и равно

.

Если же точка имеет ускорение в системе, то за время

вектор дополнительно получит приращение . Тогда

. (7)

Подставив (4) и (7) в (6) и разделив на , получим формулу

преобразования ускорения:

, (8)

где и - ускорения точки в и системах отсчета. Второе слагаемое носит название кориолисова (или поворотного) ускорения

, (9)

третье слагаемое –осестремительное ускорение

(10)

{не путать с нормальным (центростремительным) ускорением}.

Рассмотрим более общий случай, объединяющий два предыдущих.

3. Система вращается с угловой скоростью вокруг оси, перемещающейся поступательно со скоростью и ускорением по отношению к системе.

Легко понять, что формула преобразования скоростей примет следующий вид

. (11)

Формула преобразования ускорения в самом общем случае () приобретет вид:

, (12)

, (13)

где - радиус-вектор, перпендикулярный оси вращения и характеризующий положение точки относительно этой оси.

Введя обозначения , объединив члены выражения (12), не зависящие от относительного движения точки , можно написать

, (). (14)

Полученное выражение представляет собой математическую запись теоремы Кориолиса:

Абсолютное ускорение является векторной суммой относительного, кориолисова и переносного ускорений.

 

 

Основное уравнение динамики в нисо.

Из выражения (13) следует, что ускорение частицы в системе (здесь )

. (15)

Умножив обе части уравнения (14) на массу частицы и учтя, что в ИСО , получаем

. (16)

Это и есть основное уравнение динамики в неинерциальной системе отсчета, которая вращается с некоторой угловой скоростью вокруг оси, перемещающейся поступательно с ускорением .

Очевидно, что даже при частица будет двигаться в этой системе отсчета с ускорением, в общем случае отличным от нуля, причем так, как если бы на него действовали силы, описываемые членами уравнения (16). Эти силы получили название сил инерции.

Из вида уравнения (16) следует, что введение сил инерции позволяет сохранить форму записи основного уравнения динамики и для НИСО. Однако кроме силы , обусловленной действием на частицу окружающих тел, необходимо учесть и силы инерции, описываемые остальными слагаемыми в правой части уравнения (16).