4.8 Построение перпендикуляра к плоскости

Дано: ( АВС) –о.п.

К

Построить: а

1. В плоскости  проведите горизонталь h (h₂, h₁) и фронталь f(f₂, f₁).

1. Из фронтальной проекции точки К₂ опустите перпендикуляр a₂ к f_2.

2. Из горизонтальной проекции точки К₁ опустите перпендикуляр а₁ к h₁.

a₁  h₁ a₂  f₂  a 

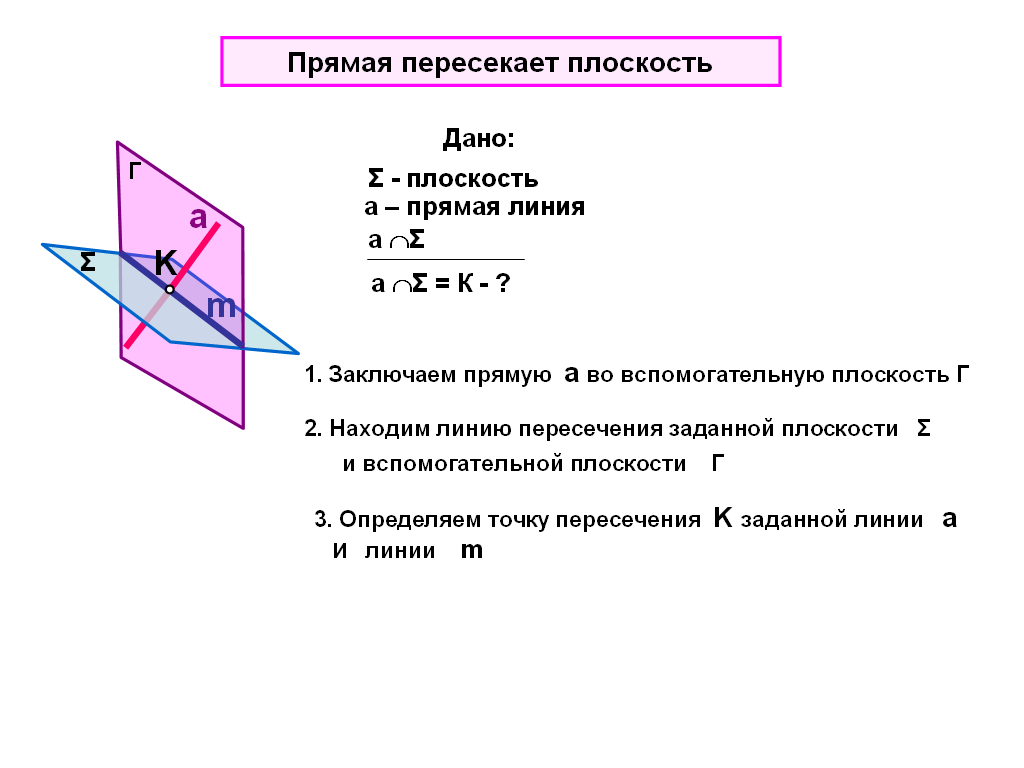
4.9 Пересечение прямой линии с плоскостью

Точку пересечения прямой линии с плоскостью общего положения строят по алгоритму:

1. Заключите прямую а во вспомогательную плоскость Г (рис.41).

2. Постройте линию пересечения m вспомогательной плоскости Г и заданной плоскости .

3. Определите точку пересечения линии m с заданной прямой а.

4. Определите видимость.

Рис. 41

4.10 Построение точки пересечения прямой с плоскостью

Дано: (АВС) –о.п.

а – о.п.

Построить: а  = К

1. Заключите прямую а во вспомогательную плоскость Г. Эта плоскость занимает фронтально проецирующее положение ГП₂ . Фронтальная проекция Г₂ совпадает с фронтальной проекцией прямой а₂.

2. Найдите линию пересечения m вспомогательной плоскости Г с плоскостью (АВС). Г = m

Фронтальная проекция m₂ совпадает с фронтальной проекцией Г₂

3. Постройте горизонтальную проекцию m_1. Для этого спроецируйте две точки 1 и 2.

4. Найдите горизонтальную проекцию точки пересечения линии (1₁-2₁) с горизонтальной проекцией прямой а₁.

(1₁-2₁)а₁ = К₁

5. Ортогонально спроецируйте точу К₂ на фронтальную проекцию прямой а₂.

6. Определите видимость прямой а на фронтальной проекции по фронтально-конкурирующим точкам 1 и 3. Эти точки принадлежат скрещивающимся прямым (АВ) и а. Их фронтальные проекции совпадают 1₂  3₂. По горизонтальной проекции, при взгляде по стрелке видно, что точка 1 - видимая, а точка 3 – невидимая. Точка 3 принадлежит прямой а, значит отрезок прямой (К₂-3₂) – невидимый, т.е. в этом месте прямая а закрыта треугольником  до точки их пересечения К.

6. Определите видимость прямой а на горизонтальной проекции по горизонтально-конкурирующим точкам 4 и 5. Эти точки принадлежат скрещивающимся прямым (ВС) и а. Их горизонтальные проекции совпадают 4₁  5₁. По фронтальной проекции при взгляде по стрелке видно, что точка 5 - видимая, а точка 4 – невидимая. Точка 4 принадлежит прямой а, значит отрезок прямой (К₁-4₁) - невидимый.

C₁