Сечение - гипербола

Рассмотрим случай, когда =0

Дано:  - прямой круговой конус

Г – секущая плоскость

Г|| i , ГП₁

Построить: линию сечения.

Секущая плоскость параллельна оси конуса, значит  = 0, т.е. линия сечения представляет собой гиперболу.

Гиперболу постройте по точкам.

1. Постройте опорные точки.

1(1₁,1₂) и 2(2₁,2₂) – точки, принадлежащие основанию конуса.

3(3₁,3₂) – точка, принадлежащая главному фронтальному меридиану и являющаяся границей видимости проекции гиперболы на П₂.

2. Постройте высшую точку гиперболы.

Высшая точка 4(4₁,4₂) строится с помощью горизонтально-проецирующей плоскости , которую проводят через ось конуса, перпендикулярно секущей плоскости Г.

 = n (n_1, n₂) – треугольник.

4n

3. Постройте промежуточные точки.

Промежуточные точки 5(5₁,5₂) и 6(6₁,6₂) строят с помощью параллелей

4. Соедините точки плавной линией (с учетом видимости).

Границей видимости на фронтальной проекции является главный фронтальный меридиан. Точки 2,5,4,3 – видимые. Точки 6 и 1 – невидимые.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1.Сформулируйте алгоритм построения линии пересечения поверхности плоскостью?

2. Что представляет собой линия пересечения многогранника плоскостью?

3. Какие линии получаются при пересечении кругового цилиндра плоскостью?

4. Какие линии получаются при пересечении кругового конуса плоскостью?

5. Какие линии получаются при пересечении сферы плоскостью и какими могут быть проекции этих линий?

ТЕСТ №8

1. В каком случае линией пересечения является эллипс?

2 В каком случае линией пересечения является треугольник?

3. В каком случае линией пересечения является парабола?

4. В каком случае линией пересечения является четырехугольник?

10. Пересечение прямой c поверхностью.

Если прямая пересекается с поверхностью тела, получаются две точки, одновременно принадлежащие как поверхности тела, так и прямой линии. Такие точки называются точками входа и выхода прямой (рис.70). Для нахождения этих точек применяется алгоритм первой главной позиционной задачи.

АЛГОРИТМ РЕШЕНИЯ ПЕРВОЙ ГЛАВНОЙ

ПОЗИЦИОННОЙ ЗАДАЧИ

1. Заключите прямую линию во вспомогательную плоскость.

2. Найдите линию пересечения вспомогательной плоскости с поверхностью заданного тела.

3. Определите точки пересечения линии сечения с данной прямой. Эти точки являются искомыми точками пересечения прямой с поверхностью.

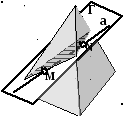
Рис.70

10.1 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ГРАННОЙ ПОВЕРХНОСТЬЮ

Дано:  - пирамида

а – о.п.

Найти точки пересечения прямой «а» с поверхностью пирамиды 

a = M,N

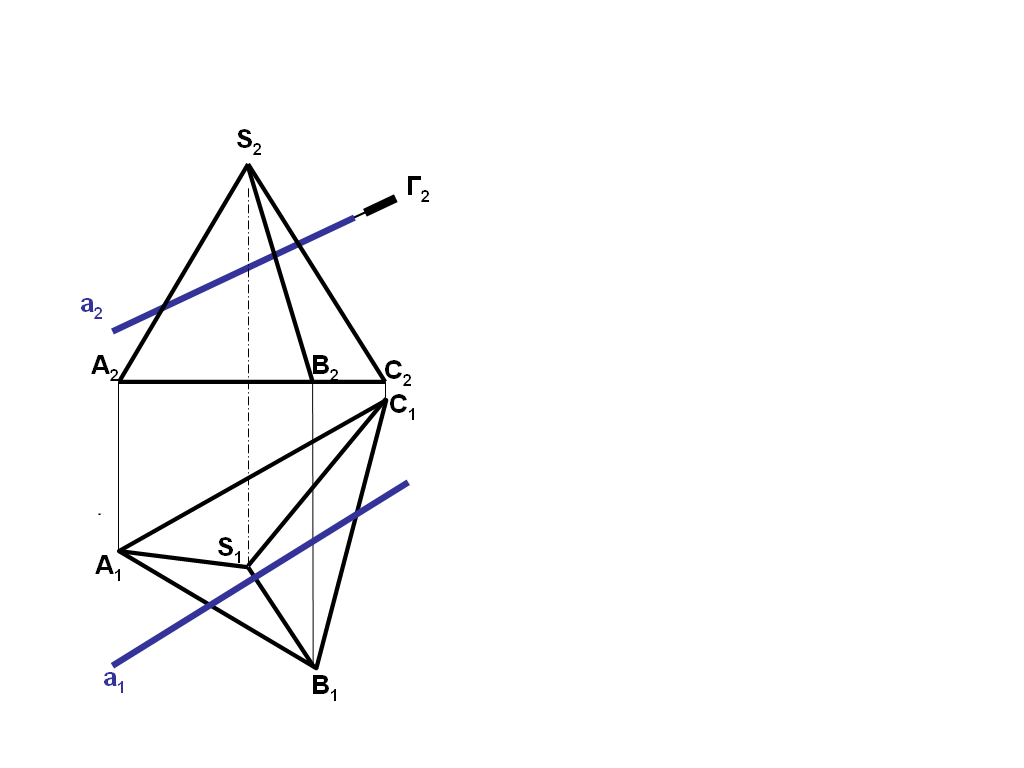
1. Заключите прямую «а» во фронтально-проецирующую плоскость Г.

а  Г

Г  П₂

2. Найдите линию пересечения плоскости Г и поверхности пирамиды .

Г = m

3. Фронтальная проекция m₂ совпадает со следом вспомогательной секущей плоскости Г. Точки 1,2,3 получены от пересечения плоскости Г и ребер пирамиды. Эти точки принадлежат линии m.

4. Линия m - треугольник (1-2-3).

Горизонтальную проекцию линии m₁ найдите ортогональным проецированием.

5.Точки пересечения горизонтальной проекции прямой а₁ с горизонтальной проекцией линии m₁ являются горизонтальными проекциями искомых точек M₁ и N₁.

6. Фронтальные проекции M₂ и N₂ найдите путем проецирования.

аm = M,N m

а = M,N

7. Определите видимость.

10.2 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЬЮ

ВРАЩЕНИЯ

Задан прямой круговой конус . Прямая а общего положения пересекает конус в двух точках (рис.71). Для построения этих точек воспользуйтесь алгоритмом первой главной позиционной задачи:

Вспомогательную плоскость, проводимую через прямую, стремятся выбрать так, чтобы она пересекала кривую поверхность по линии, простейшей для построения на чертеже - прямой или окружности.

1.Заключите прямую а во вспомогательную плоскость общего положения  (с  b), проходящую через вершину конуса S.

2. Постройте линию пересечения плоскости  с поверхностью конуса 

= (5-S-6) – треугольник.

3. Найдите точки пересечения прямой a с линией (5-S-6).

а  (5-S-6)= M,N

Точки M,N являют искомыми точками пересечения прямой a с поверхностью конуса .