Определить двугранный угол

Дано:

(ABC)

(ABD)

Для определения линейного угла , измеряющего двугранный угол, достаточно расположить его так, чтобы ребро [АВ] оказалось перпендикулярным плоскости проекций.

1.Преобразуйте ребро [АВ] общего положения в прямую уровня, применив первую основную задачу преобразования комплексного чертежа.

П₂ П₄  П₁ ; П₄ || [AB]

X₁₂ X₁₄|| [A₁B₁]

2.Преобразуйте ребро [АВ] в проецирующую прямую, применив вторую исходную задачу.

На плоскости проекции П₅ ребро [AB] вырождается в точку, а грани АВС и АВD вырождаются в отрезки прямых.

На П₄ линейный угол  спроецируется в натуральную величину.

П₁ П₅  П₄

П₅  [AB]

 = , 

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1.Зачем необходимо преобразование комплексного чертежа?

2. Какие основные задачи решаются путем преобразования чертежа?

3. В чем сущность способа замены плоскостей проекций?

4. Как надо расположить новые плоскости проекций, чтобы отрезок прямой общего положения спроецировался в натуральную величину, в точку?

5. Как нужно расположить новую плоскость проекций, чтобы плоскость общего положения стала проецирующей?

ТЕСТ №7

1. На каком чертеже введена плоскость П₄ для определения

угла наклона отрезка (АВ) к П₁?

2. На каком чертеже в результате замены будет определен угол

наклона отрезка (АВ) к П₂?

3. На каком чертеже одной заменой возможно преобразование

прямой в проецирующее положение?

4На каком чертеже для преобразования прямой в

проецирующее положение ось задана неверно?

9. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПЛОСКОСТЯМИ

Сечением называется плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.

Плоскости, которые образуют сечения, называют секущими. Плоскость, пересекая поверхность многогранника, дает сечение в виде многоугольника. Вершинами такого многоугольника являются точки пересечения ребер многогранника с секущей плоскостью, а сторонами – прямые линии пересечения граней с секущей плоскостью (рис.66).

 - пирамида

Г – секущая плоскость

MNK – сечение (треугольник)

Рис.66

Рис.67

Плоскость, пересекая кривые поверхности, в общем случае дает криволинейную фигуру (окружность, эллипс и т.д.) (рис.67).

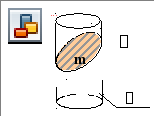
 - цилиндр

 – секущая плоскость

m- линия сечения (эллипс)

Построение линий сечения поверхности плоскостью значительно упрощается, если секущая плоскость является проецирующей. В этом случае одна из проекций линии сечения совпадает с проекцией проецирующей плоскости.

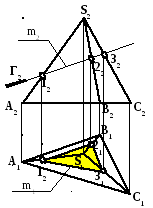
9.1 Пересечение пирамиды проецирующей плоскостью

Построить линию пересечения

пирамиды  плоскостью Г

Дано:  - пирамида

Г- плоскость

ГП₂

Построить: Г=m

1.Фронтально проецирующая плоскость Г пересекает три ребра пирамиды:

ГSA=1

ГSB=2

ГSC=3

m = (1-2-3)

Фронтальная проекция линии пересечения m ₂(1₂-2₂-3₂) совпадает с фронтальной проекцией Г₂

2. Горизонтальные проекции линии (1₁-2₁-3₁) получают с помощью вертикальных линий связи, перенося все точки с фронтальной проекции на горизонтальную проекцию.

3. Соединяя последовательно точки 1₁,2₁,3₁ отрезками прямых, получают горизонтальную проекцию линии сечения.