§29. Большое каноническое распределение

Запишем первое начало термодинамики, при учёте, что происходит обмен частицами:

где - число частиц, а- химический потенциал.

Пусть между системами 1 и 2 идёт обмен частицами (материальный контакт) и энергетический контакт (теплой обмен).

Для энтропии можем записать:

Ранее мы писали соотношение:

Теперь добавим туда и перепишем его:

Поступая аналогично случаю теплового контакта, мы получаем, что равновесие при тепловом и материальном контакте наступает при

и, т.е.

и

Аналогично получают большое каноническое распределение:

система находится в квантовом состоянии и имеетчастиц.

В данном случае система находится в тепловом и материальном контакте.

Еще большое каноническое распределение называют распределением Гиббса с переменным числом частиц.

Здесь статистическая сумма и.

- набор квантовых чисел, характеризующих состояние системы.

§30. Термодинамический потенциал Гиббса

В термодинамике есть следующее понятие:

-свободная энергия Гельмгольца

- свободная энергия Гиббса.

-термодинамический потенциал Гиббса, он играет важную роль в связи с большим каноническим распределением.

здесь - статистическая сумма канонического распределения, а- статистическая сумма большого канонического распределения.

Запишем первое начало термодинамики:

Используя большое каноническое распределение, рассчитаем энтропию:

Теперь переходим в термодинамику, т.е. опускаем знак для средних:

Отсюда имеем:

Запишем выражение:

Подставим сюда выражения для первого начала термодинамики, тогда получим:

(17)

Аналогично получим .

Подставим сюда выражение для :

(18)

Нетрудно показать, что

Из соотношений (17) и (18) видно, функциями каких переменных являются функции и:

Переход от одной функции к другой идёт с помощью преобразования Лежандра, т.е. переходя от одних переменных к другим.

Из полученных нами выражений вытекают определения:

Из (17) имеем

, здесь

Из (18) имеем:

, здесь

- это интенсивный параметр, т.е. при равновесии системы он выравнивается.

- это экстенсивный параметр, он аддитивен, поэтому в статистической физике соотношение дляпишется так:

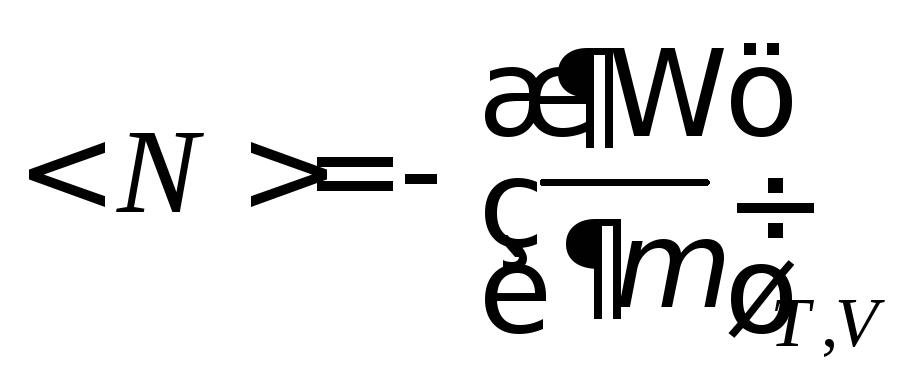
§31+. Распределение Больцмана как следствие большого канонического распределения Гиббса

Будем рассматривать идеальный газ, где частицы взаимодействуют между собой очень слабо или совсем не взаимодействуют: частицы могут либо слабо взаимодействовать, либо газ настолько разрежён, что частицы находятся друг от друга далеко, потому и слабо взаимодействуют.

В распределении Больцмана рассматриваются разреженные газы, т.е. здесь условие:

это вероятность реализации - того одночастичного состояния счастицами.

Среднее число частиц:

Но для распределения Больцмана используют ограничение - в силу разреженности газов.

Тогда наибольшая из вероятностей :

- что в-том состоянии нет частиц, потом идёт- вероятность того что в-том состоянии одна частица, и т.д.

Поэтому пишем , а остальными слагаемыми можно пренебречь.

, т.к.

Тогда имеем:

Можем записать , тогда:

, где

Для вероятностей иможем записать. Найдёми.

Для мы уже писали:

, где

Найдём :

, где

Т.к. условие нормировки для выполняется, то его можно записать с точностью до двух слагаемых:

Тогда

Следовательно, мы можем записать:

Перейдём к распределению Больцмана.

Дальше будем писать строгие равенства.

,

Рассмотрим квазиклассическое приближение. Одночастичное состояние будет описываться функцией , где состояние характеризуется фазовой точкой в фазовом пространстве, а не индексомсостояния.

Соответственно возникает число состояний приходящихся на элементарный объём:

здесь - объём элементарной ячейки, приходящейся на одно состояние в квазиклассике.- это число степеней свободы приходящихся на одну частицу.

Для системы частиц писали:

А у нас в данном случае:

Мы будем рассматривать случай, когда ( т.е. 3 степени свободы) - это одноатомная частица, тогда:

Итак, переходим от среднего числа в состоянии , к среднему числу частиц приходящихся на этотфазовый объём. Тогда число частиц в элементарном объёме:

в этом выражении от перешли к, т.е. энергия здесь утратила индекс состояния.

Поделим на число частиц , тогда мы найдём вероятность того, что частица находится в элементарном объёме фазового пространства:

вероятность того что состояние частицы лежит в элементарном объёме шестимерного фазового пространства , т.е.

импульс и координаты частицы попадают в эти интервалы.

Если нормировать эту вероятность по координатам или по импульсам, то переходим к распределению по координатам либо по импульсам.

Можем записать

Видим, что энергия разбивается на два слагаемых. В силу этого разбиения можем записать:

- распределение Максвелла

- распределение Больцмана

Можем с помощью этих функций находить средние и т.п.

Можно их записать на языке числа частиц: