§15. Микроканоническое распределение Гиббса

Рассматриваем замкнутую систему, и согласно принципу равной вероятности, все состояния системы, с заданной энергией , равновероятны.

Причём, т.к. система находится в состоянии со средним значением энергии, то

Для того чтобы получить распределение, учитывающее флуктуации энергии, мы используем теорему Лиувилля и перейдём к каноническому распределению Гиббса.

§16. Каноническое распределение Гиббса

Удобно записать теорему Лиувилля в виде:

- есть интеграл движения, точнееесть функция различных интегралов движения.

Поместим систему в жёсткий неподвижный ящик, тогда, т.к. не может двигаться так: , то нет сохранения импульса. И так как не может вращаться , то нет сохранения момента импульса. Тогда осталось сохранение энергии, т.е. можем записать:

Само распределение пишется:

Это каноническое распределение Гиббса; для квантового случая навешивается - номер квантового состояния.- константа, не зависящая от состояния, которая находится из условия.

Здесь - температура в энергетической шкале – это удобно в теории. Хотя на практикеизмеряют в градусах.

,

тогда .

§17. Принцип возрастания энтропии

Наиболее вероятным развитием системы является такое, при котором полная производная энтропии больше нуля:

(*)

Этот принцип сформулировал Клаузиус.

Имея этот принцип, можем получить соответствующее распределение.

Условие (*) означает, что если система выведена из состояния равновесия, то она движется к равновесию по этому закону.

Тогда в состоянии равновесия энтропия системы экстремальна (max)

Так как условие имеется условие нормировки, то имеем условный экстремум, а если бы не было условия нормировки, то был бы абсолютный экстремум.

§18. Микроканоническое распределение Гиббса (продолжение)

Аналогом соотношения для квантовых систем является соотношение:

Для замкнутых квантовых систем энергия системы – константа, тогда имеет место принцип равной вероятности всех микросостояний, которые отвечают данному значению энергии системы, тогда

, а значит

- это вероятность реализации-го состояния с энергией.

Но т.к. все состояния равновероятны:

- номер подсистемы.

§19. Каноническое распределение Гиббса

Система 1 и термостат 2 образуют замкнутую систему. Здесь присутствует микроканоническое распределение.

На базе микроканонического распределения строят каноническое распределение.

Также можно получить каноническое распределение системы через принцип возрастания энтропии.

Рассмотрим систему 1, и считаем что состояние стационарное.

Найдём условие экстремума функции .

Мы используем - квантовые функции, т.к. это удобнее, чем использовать. При использованиивылезает константа из-за размерности.- это размерная величина, а логарифм надо брать от безразмерной величины, каковой и является.

Второе начало термодинамики:

т.е. если система выведена из состояния равновесия, то она идёт в развитии с увеличением , поэтому:

- имеем условие экстремума

Отсюда имеем задачу поиска экстремума функции .

Вероятность удовлетворяет условию нормировки:

-это условие для отыскания экстремума

Задача (1) и (2) является задачей поиска условного экстремума.

Однако с помощью метода неопределённых множителей Лагранжа можно найти экстремум . Для этого вводится функция

, где

Найдём производную :

здесь остальные члены при дифференцировании обращаются в нуль.

Найдём вторые производные:

, при

- это выражение отрицательное

Стало быть, мы имеем максимум, так как вторая производная меньше нуля.

Тогда из условия находим само условие экстремума.

константа находится из условия нормировки:

, где- число всех состояний

Выражение (*) есть принцип равной вероятности для замкнутой системы; это есть микроканоническое распределение.

Теперь найдём экстремум энтропии при двух условиях, а именно при:

и

Переходим от условного экстремума энтропии к безусловному экстремуму функции :

Берём производные:

(3) - это условие экстремума , это одно и то же что условие экстремума дляпри условияхи.

Обозначим , тогда:

Отсюда для имеем:

Постоянная находится из условия нормировки:

(5)

Выражение (5) называется статистической суммой. А выражение (4) – это каноническое распределение Гиббса.

Это распределение относится к системе:

Где 1 находится в тепловом контакте с термостатом 2.

Микроканоническое распределение мы получали для замкнутых систем, где , т.е. условияивырождаются в одно. И для микроканонического распределения мы получили:

А каноническое распределение получили, когда система 1 была в тепловом контакте с термостатом 2:

Константа находится из условия, т.е.- здесьсреднее значение энергии, т.к. у нас случай термодинамики.

Найдём связь энтропии с энергией:

Тогда:

Используем условия и:

- это константа по энергии.

В термодинамике - это наблюдаемая величина, поэтому пишут эту величину просто, т.к.(- из эксперимента, а- из теории).

Тогда:

Отсюда имеем , но ведь, а значит:

И мы определили второй неопределённый множитель Лагранжа.

Каноническое распределение Гиббса принимает вид:

, где

Аналогично пишут для , но тогда вместо статистической суммыбудет интеграл.

Здесь - температура в энергетических единицах.

§20+. Флуктуации аддитивных величин

Рассматриваем величины, которые для всей системы связаны с аналогичными величинами подсистем по закону суперпозиции:

,-номер подсистемы,-число подсистем

Под , например, можно приближённо понимать энергию, когда подсистемы квазизамкнуты, статистически независимы.

Статистическая независимость означает, что исистемы выражаются произведением по соответствующим функциям подсистем:

и(6)

Для таких функций упрощается расчёт средних значений случайных величин, которые описываются этими функциями.

Мы будем рассматривать флуктуации .

Часто мерой флуктуации выступает дисперсия:

или относительное среднеквадратичное отклонение:

Следствием вида функций (6) имеем:

,иэто разные подсистемы

Это свойство можно легко доказать, если использовать вид этих функций, где определение среднего по непрерывному фазовому пространству:

тогда используя (6) получаем: ,- вероятности отдельных подсистем.

Если рассмотреть , то:

иесть среди коэффициентов, т.е.иэто подсистемы из множества всех подсистем, тогда:

, аи

Можно писать , но записьсоответствует вообще-то такому виду записи, асоответствует такому

Теперь рассмотрим такое же среднее, но для флуктуаций величин:

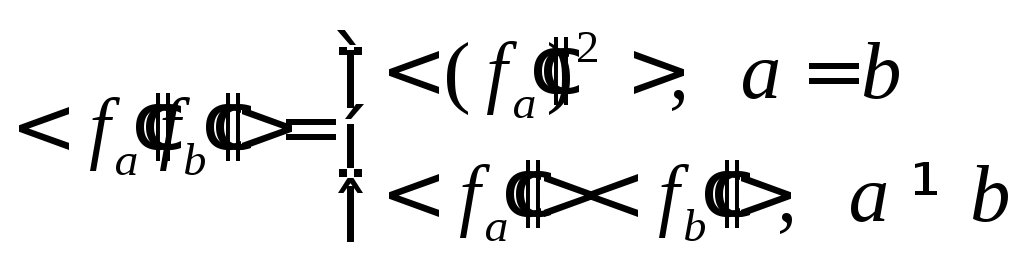
Учтём, что:

- дисперсия случайной величиныв подсистеме

Тогда с учётом этих равенств получаем:

(7)

Посмотрим среднее от аддитивной наблюдаемой случайной величины:

,- число подсистем.

Знак примерного равенства объясняется так:

Если разбиение системы на макроскопические подсистемы таково, что они примерно равны, то говорят, что тоже примерно равны между собой для каждой подсистемы, т.е. получаем, чтоне зависит от номера подсистемы.

Аналогично найдём дисперсию:

т.к. - сумма, то и, тогда:

Используем равенство (7), тогда:

т.е. дисперсия тоже обладает свойством аддитивности, и можно говорить, что имеет место соотношение:

Найдём :

Если исходная система достаточно велика, то число - можно сделать достаточно большим, поэтому:

,- число частиц в системе.

Величина служит мерой вероятности отклонения величиныот её среднегоили, если учитывать эргодическую гипотезу, то это есть относительное время пребывания системы когдаотлично от, где- параметр системы. Для достаточно больших систем, поэтому система почти всё время пребывает в состоянии с параметром- с наиболее вероятным параметром.

§21+. Энтропия и статистический вес

Запишем определение энтропии:

Для канонического распределения мы установили:

здесь мы учитывали только один аддитивный интеграл движения .

Тогда:

, но

- к этому привела Аддитивность и теорема Лиувилля.

Тогда , где- это вероятность состояния с энергией, т.е. это равновесное состояние.

Оценим .

При рассмотрении квантовых систем энергетические уровни образуют дискретное множество точек. Но для достаточно больших систем эти точки расположены достаточно плотно, и можно перейти к непрерывному распределению, т.е. мы «размазываем» дискретный спектр по непрерывному. В этом нет ошибки. Переходим от к

Вводят

Запишем нормировку для ,переходит в, гдеэто число состояний в интервале.

Вводят обозначение - это плотность реализации состояния с энергией, т.е. из интервала.

Из малости имеем, что система большую часть времени пребывает в состоянии с энергией, а вероятность пребывания в состояниях с энергией не равнойочень мала. Поэтому вид распределения:

Площадь под этой кривой можно рассчитать, зная величину.

Параметруможно поставить в соответствие параметр:

, но

тогда:

(8)

Величина , найденная таким образом, называется статистическим весом.

Вероятность мультипликативна,- аддитивна.

Мы установили связь (8) энтропии и статистического веса, тогда - оценка статистического веса.

Энтропия определяется через статистическое среднее. Это означает, что мы должны иметь достаточно большой по численности ансамбль систем, и провести усреднение. С другой стороны, если справедлива эргодическая гипотеза, то .

Здесь статистический подход требует, чтобы время наблюдения было достаточно большим.

Энтропия это статистический параметр, и все параметры, определяемые через энтропию тоже статистические, т.е. они должны определятся на системах с большим числом частиц(с большим числом степеней свободы).

§22+. Температура. Статистическое определение. Условие равновесия систем, находящихся в тепловом контакте

Мы ввели определение температуры, используя первое начало термодинамики:

- причём это в равновесном состоянии

Температура выражена через энтропию, а энтропия это статистический параметр, поэтому это тоже статистический параметр.

Запишем энергию для системы 1 + термостат 2. Здесь вся система в целом – замкнутая.

Можно записать .

Рассмотрим случай, когда система выведена из состояния равновесия. Система будет переходить в равновесное состояние и энтропия системы должна возрастать при этом переходе:

Тогда:

изависит отчерез. Мы рассматриваем только тепловой (или энергетический) контакт.

Равновесие системы может наступать через приход в равновесие отдельных подсистем. Так как система целиком замкнутая, то , и тогда, а значит

Тогда получаем:

(9)

Процесс установления равновесия описывается неравенством (9). Из этого неравенства имеем:

Отсюда видим, что если , то, т.е. идёт перекачка энергии от 2 к 1 подсистеме, т.е. идёт повышение температуры в 1 подсистеме.

Когда достигает максимума, т.е. имеем установление равновесия, то:

Это есть условие равновесия 1 и 2 подсистем.

§23+. Статистическая сумма и её свойства

Мы определили каноническое распределение:

,

и - это сумма по состояниям, а не по энергетическим уровням.

Энтропия:

Тогда, учитывая язык термодинамики , получаем:

Введём свободную энергию Гельмгольца:

Тогда

(10)

Получаем, что определяется через:

Тогда можем записать:

Из (10) получаем:

Мы будем часто использовать это равенство (здесь в энергетических единицах).

Используем определение для нахождения. Запишем определение среднего:

Эту сумму можно найти, используя дифференцирование по параметру :

Но ведь , тогда:

Используем равенство (10):

Тогда:

А в духе термодинамики , тогда:

Мы получили связь между энергией и свободной энергией Гельмгольца.

Мы получили связь между энергией и статистической суммой, где

, а

Запишем определение :

Найдём . По определению:

Подставим сюда выражение для и получим:

, здесь сумма – это сумма по состояниям.

Используем дифференцирование по параметру :

Тогда наше выражение примет вид:

По определению , тогда:

Раньше мы получили соотношение

Тогда:

(11)

Покажем, что равенство верно:

Выражение (11) можно связать с :

Ранее мы получили, что:

Тогда:

Теперь, если пишем это равенство для термодинамики, то и

Величина - это теплоёмкость при постоянном объёме (в термодинамике). Это теплоёмкость всей системы.

Тогда:

- линейная аппроксимация

здесь - безразмерная, а- температура в энергетических единицах.

Удельная теплоёмкость – это теплоёмкость в расчёте на единицу массы.

-теплоёмкость в расчёте на одну частицу

Тогда:

Отсюда следует не отрицательность теплоёмкости .

§24+. Функция распределения вероятностей по энергии и распределение Гаусса

Поскольку величина относительного среднеквадратичного отклонения для энергии значительно меньше 1:

то функция распределения этой величины(энергии) описывается узкой функцией с максимумом:

Ширина максимумаочень мала, т.к..

Так как максимум резкий, то часто эту функцию распределения аппроксимируют Гауссовым распределением:

Константы илегко находятся.

- из условия нормировки:

Тогда:

Интеграл является табличным.

Окончательно для получаем:

Найдём константу через:

Используем дифференцирование по параметру, где мы обозначим :

Но , тогда:

Очевидно, что , т.к.:

-чётная

-как нечётная функция в симметричных пределах

Имеем тогда для :

(12)

Т.к. , то удобно записывать выражение (12) так:

(13)

где .

Зависимости (12) и (13) разные, это надо помнить.

Тогда можно написать:

Окончательно получаем:

Когда мы писали - то получали центрированную случайную величину.

Перейдём к нормированным функциям, т.е. перейдём от . Обозначим, тогда от функциипереходят к:

(14)

здесь для случайной величины :

и

Выражение (14) – это функция Гаусса, в ней всё удобно считать.