Метод конечных элементов.

Сущность метода заключается в расчленении конструкции на отдельные стержни, с целью анализа, с последующим соединением их в единое целое в процессе синтеза. Сопряжение элементов осуществляется на основе составления трех групп уравнений:

1. Статических, описывающих равновесное состояние элементов системы;

2. Геометрических, устанавливающих связь между деформациями элементов и перемещениями их узлов;

3. Физических, связывающих между собой силы и деформации.

Для простоты рассмотрим плоскую стержневую систему, нагруженную узловыми сосредоточенными силами и моментами.

М₃ Р₄

3 4

4

2

Р₁

1

6

1 2

5 6 7

Пронумеруем узлы и стержни в произвольном порядке. Обозначим число узлов u, число стержней S. Мысленно выделим из рамы произвольный k стержень, соединяющий узлы i, j.

ξ

l_k N_j

M_j

Q_i

_y

N_j

k

_j

P_xj

N_j

Q_j

P_yj

α

Q_i

M_{i i x}

N_i y

Q_i

_i

N_i

x

M_i

P_ui

P_xi

Вводим 2 системы координат: общую XY и местную ξ. Следуя общему плану решения задач прочности, рассматриваем анализ, состоящий из трех сторон задачи: статической, геометрической и физической.

1. Статическая сторона задачи.

Установим зависимость между внешними нагрузками, приложенными к узлам ij и внутренним усилиям в стержне k.

В левом сечении стержня возникают внутренние усилия N_i, Q_i, M_i, которые мы объединим базовым вектором усилия для k стержня.

где индекс т означает транспонирование вектора или матрицы, когда столбцы меняются местами со строчками.

Будем считать, что внутренние усилия в сечениях, примыкающих к узлам, уравновешиваются некоторой частью внешних нагрузок P_x, P_y, M^e, приложенных к узлу. Обозначим вектора частью внешних нагрузок в узлах i, j

Объединим их базовым вектором нагрузок для k стержня.

Эти внешние нагрузки создают внутренние усилия.

Составим уравнения равновесия для узла i.

Из условий равновесия стержня получаем:

Рассматривая условия равновесия узла j, аналогично узлу i, получаем с учетом равенств (*).

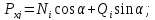
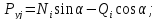
В матричной форме эти зависимости имеют вид:

где 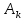- матрица преобразования при переходе из местной системы координатв общуюXY.

Этой зависимостью устанавливается связь между внутренними усилиями в начале стержня и внешними нагрузками в узлах его примыкания (базовыми векторами внутренних усилий и базовыми векторами узловых нагрузок).

2. Геометрическая сторона задачи.

Установим зависимость между перемещениями узлов i, j и абсолютными деформациями стрежня k. Введем базовый вектор абсолютной деформации:

Где - деформация, соответствующая продольной силеN_i (удлинение);

- деформация, соответствующая поперечной силе Q_i (сдвиг);

–деформация, соответствующая изгибающему моменту M_i (поворот).

Базовый вектор перемещений узлов обозначим:

Где - перемещения узлов по осих, - перемещения узлов по осиy, и- углы поворота узлов.

Если известны перемещения узлов, то через них можно выразить деформации. Эти геометрические соотношения более сложны при выводе, чем статические уравнения. В векторной форме эту зависимость можно представить по аналогии с зависимостью (1): т.е.- некоторая матрица преобразования.

Чтобы более просто установить вид этой матрицы, воспользуемся принципом Лагранжа: если механическая система находится в равновесии, то сумма работ внешних и внутренних сил равна нулю. В качестве возможных можно принимать действительные перемещения, если они достаточно малы.

Работа внешних сил совершается на перемещениях узлов, а работа внутренних усилий – на абсолютных деформациях. Работа внутренних сил на действительных деформациях всегда отрицательна, поэтому можно записать, учитывая, что стержень рассматривается в положении равновесия:

i j

l₀

r_ij r_ji

д

Подставляя в равенство формулы (1) и (2), получаем:

.

Так как слева и справа стоят одинаковые вектора, то или

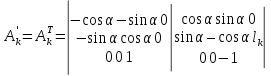
Таким образом,

3. Физическая сторона задачи.

Мы установили статические (1) и геометрические (2а) зависимости. Для того, чтобы согласовать их между собой, воспользуемся законом Гука (какова деформация, такова сила, какова сила, такова деформация).

Где элементы 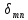матрицыесть абсолютные деформации по направлениюm обобщенной силы, вызыванные действием единичной обобщенной силы в n направлении.

Рассмотрим схему стержня, эквивалентную заданной:

M_i F₁=N_i;

N_i

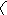
Q_i l_k F₂=Q_i

F₃=M_i

При действии продольной силы стержень удлиняется на, т.к.

При действии поперечной силы стержень изгибается, образуя прогиб и угол поворота.

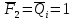
При действии изгибающего момента стержень так же изгибается, образуя прогибы и угол поворота.

Матрица B_k принимает вид:

Закон Гука можно записать в прямой форме (какова деформация, такова сила):

где обратная матрица имеет вид:

Подставим зависимость (3) и (2а) в (1) () и получим:

Где - матрица жесткости дляk стержня, имеющего узлы i, j. В развернутом виде матрицу жесткости стержня для случая α=0 () можно записать так:

Анализ отдельно взятого стержня закончен. Можно переходить к синтезу, т.е. к рассмотрению всей системы в целом. Исходные данные следующие:

1. Координаты узлов системы – геометрическая информация;

2. Жесткости поперечных сечений стержней – физическая информация;

3. Стержневая связь между узлами – топологическая информация;

4. Внешние нагрузки – статическая информация.

Требуется определить:

1. Усилия во всех стрежнях;

2. Перемещения всех узлов.

Обозначим: – вектор узловых нагрузок системы;

- вектор внутренних усилий системы;

- вектор узловых перемещений системы;

- вектор абсолютных деформаций системы;

А – матрица равновесия системы;

В – матрица податливости системы;

R – матрица жесткости системы.

Для поставленной задачи имеем:

1. Уравнения равновесия

2. Геометрические уравнения

3. Физические зависимости закона Гука

Так как в число неизвестных входят только усилия и перемещения, то исключим из трех видов уравнений вектор деформации. Подставим (а), (б), (в):

Объединим уравнения (а) и (г) в одну систему:

(д)

Матрица А имеет 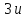строк и 3S столбцов (u – число узлов, S – число стержней). Матрица имеет 3S строк и столбцов.

Первое векторное уравнение содержит 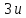алгебраических уравнений с 3S неизвестными, а второе векторное уравнение - 3S алгебраических уравнений с неизвестными. Всего уравнений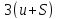; число неизвестных так же равнокаждый узел имеет 3 перемещения, а каждый стержень 3 усилия.

Выразим из второго векторного уравнения вектор усилий

Подставим в первое векторное уравнение:

где - матрица жесткости системы.

Решая уравнение с 3u неизвестными 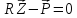находим перемещения всех узлов системы:

Затем вычисляем усилия во всех стержнях системы: