Теорема Кастильяно о взаимности энергии и перемещений

Частная производная от потенциальной энергии по какой-либо внешней силе равна перемещению по направлению этой силы.

Пусть к упругой конструкции приложено n сосредоточенных сил P_i.

P₁ P₂ P_i P_n

Изгибающий момент в произвольном сечении выразим на основе принципа суперпозиции:

где – изгибающий момент от действия единичной силы=1.

Найдем частную производную от изгибающего момента по силе P_i:

Потенциальная энергия деформации равна:

Возьмем частную производную от энергии по силе P_i:

Теорема Рэлея о взаимности реакций

Реакция в связи 1, возникающая при перемещении связи 2, равна реакции связи 2, возникающей при перемещении связи 1, при условии, что перемещения связей одинаковы.

В качестве примера покажем раму, имеющую 5 связей: 3 в заделке и 2 в шарнирной опоре. Пусть I связь будет горизонтальная в шарнире, а II связь – угловая в заделке.

B В R₁₂

R₁₁

( ) перегиба ∆₁=∆

( ) перегиба

Первое состояние системы Второе состояние системы

А A

R₂₁ R₂₂ ∆₂=∆

Рассмотрим два состояния системы. В I состоянии происходит перемещение шарнира В по горизонтали на величину ∆. В результате того, что рама статически неопределима во всех опорных связях, появляются опорные реакции, противодействующие перемещению. Обозначим реакции в выделенных связях R₁₁ и R₂₁. Первый индекс показывает в какой связи возникает реакция, а второй – от смещения какой связи она возникает.

Во II состоянии даем угловое перемещение заделки А на величину ∆. Соответствующие реакции обозначим R₁₂ и R₂₂. Воспользуемся теоремой о взаимности работ: или.

При записи выражений для возможных работ, силы необходимо брать в одном состоянии, а перемещения по их направлению – в другом состоянии.

Правило Верещагина для перемножения эпюр

Произведение двух эпюр, хоть одна из которых прямолинейна, равно площади криволинейной эпюры, умноженной на ординату прямолинейной эпюры, взятой под центром тяжести криволинейной.

При вычислении перемещений по формуле Мора, каждый раз приходится составлять общие выражения для внутренних усилий (изгибающих моментов) на каждом участке от внешних нагрузок и единичных сил, а затем производить интегрирование произведения двух алгебраических функций. Подынтегральная функция имеет вид многочлена, редко превышающего третью степень.

Это объясняется тем, что при воздействии на систему сосредоточенных сил, выражения для изгибающих моментов имеют линейную зависимость вида: M=b₀+kz, а при воздействии, кроме указанных выше, так же и равномерно-распределенных нагрузок, выражения имеют квадратичную зависимость: M=a+bz+cz².

Графически эти зависимости отображаются соответственно наклонной прямой и квадратной параболой, и называются эпюрами моментов. Необходимо заметить, что в единичном состоянии эпюра моментов всегда линейна, а в грузовом состоянии эпюраможет быть прямолинейной или параболической.

Таким образом, на каждом участке необходимо вычислить интеграл

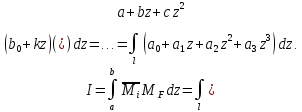
Является целесообразным произвести это интегрирование в общем виде и использовать полученное правило при решении конкретных задач.

Рассмотрим наиболее общий случай: грузовая эпюра – парабола или любая другая криволинейная фигура; единичная эпюра – прямолинейная трапеция: M_i=b+kz, где b – начальная ордината эпюры, - угловой коэффициент,- угол наклона эпюры.

Грузовая эпюра M_F:

M_F(Z) ω_MF

dω_MF C_MF

z dz

M_i(Z)

Z_CMF

Единичная эпюра

M_i(Z_CMF)

b α

l

ω_MF – площадь грузовой эпюры

C_MF – центр тяжести грузовой эпюры.

Разобьем интеграл 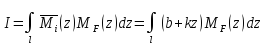на два подинтеграла:

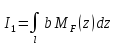и

ω_MF – площадь грузовой эпюры, S_MF – статический момент площади грузовой эпюры относительно оси, проходящей через начало эпюры. Его можно вычислить, зная площадь и абсциссу центра тяжести.