
ZO-2008
.pdf
Анализ и решение
1. Поверхность проводника является эквипотенциальной поверхностью. На этом свойстве проводников основан метод зеркальных изображений, позволяю- щий рассчитывать различные электростатические поля. Суть метода заключается в следующем. Если в произвольном электростатическом поле заменить эквипо-
тенциальную поверхность проводящей поверхностью такой же формы и создать на ней такой же потенциал, то данное электростатическое поле не изменится.
При внесении металлической пластины в поле положительно заряженного
кольца E на ней появляются индуцированные заряды, причем, на поверхности, обращенной к кольцу, индуцируются отрицательные заряды с поверхностной плотностью – σ инд. Напряженность поля индуцированных (отрицательных) заря-
дов вблизи проводящей пластины находится по формуле
Eинд = |
|
σ инд |
, |
|
|
||
|
|
ε0 |
|
где σ инд – поверхностная плотность индуцированных на пластине зарядов. Эту формулу нетрудно вывести с помощью теоремы Гаусса (см. пример из Темы 11).
Электростатическое поле между заряженным кольцом и пластиной, согласно методу зеркального изображения, эквивалентно полю, созданному данным коль- цом и его зеркальным изображением в пластине. Это поле может быть рассчитано по принципу суперпозиции.
E = E к + Eизобр.к
где Eк , Eизобр.к – напряженности полей кольца и его изображения в данной точке.
Найдем напряженность кольца Eк . Выделим на нем элемент длины dl, с за- рядом dQ.
dQк |
O |
|
R |
|
Qк |
|
|
|
|
|
|||
|
|
dQ |
|
|
dEх Х |
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ϕ = const |
|
|
|||
r |
|
h |
|
|
|
|
h |
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
dE |
|
||||
|
|
|
|
|
|
|
|
||||||
dE |
x |
|
|
|
|
dEx |
X |
R |
Eизобр.к |
|
|||
r |
|
|
|
|
|
|
ϕ = const |
|
|
dQизобр.к |
|||
|
|
|
|
|
r |
|
|
|
|
|
|
||
dE* |
|
|
r |
к |
dE |
|
|
У |
|
−Q |
изобр.к |
||
|
|
|
|
|
|||||||||
|
|
|
E |
|
|
|
|
|
|
||||
У
Этот заряд создает в данной точке поле, напряженность которого можно рас-
считать по формуле
r |
|
||||
dEк = k |
dQ |
|
r |
, |
|
r2 r |
|||||
|
|
||||
51

здесь k = 4πε1 0 , ε0 – диэлектрическая постоянная, r – радиус-вектор, направлен-
r
ный от элемента длины dl к точке поля, где вычисляется напряжённость, r = r .
Чтобы найти напряженность поля, созданного всем кольцом, необходимо сложить (проинтегрировать) напряженности от всех его элементов. При этом сле- дует учесть, что слагаемые являются векторами и имеют различные направления. Совместим начало системы координат ХУ с точкой, где ищется результирующее поле. Проекции векторов напряженностей полей, создаваемых какой-либо парой заряженных элементов кольца dl, лежащих на одном диаметре, на ось Х склады-
ваясь, компенсируют друг друга, а на ось У – дают результирующее поле dEк . |
|||||||||||||
Таким образом, вектор напряженности поля создаваемого всем кольцом Eк будет |
|||||||||||||
направлен по оси кольца, а его модуль |
|
|
|
|
|
cosα |
|
|
|
|
|||
Eк = Eyк = òdEкcosα = òk |
dQ |
òdQ = k |
Q |
||||||||||
|
|
|
cosα = k |
|
|
|
|
cosα . |
|||||
|
r |
2 |
r |
2 |
r |
2 |
|||||||
Q |
Q |
|
|
|
|
|
|
Q |
|
|
|||
Совершенно аналогично находится напряженность поля изображения кольца |
|||||||||||||
|
Eизобр.к |
= k |
Q |
cosα . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
Итак, результирующая напряженность электростатического поля кольца и его
изображения в данной точке
E = Eк + Eизобр.к = 2k rQ2 cosα .
Индуцированные заряды распределяются по пластине так, что их поле внут- ри пластины компенсирует внешнее поле (напряженность поля внутри проводни- ка, расположенного в электростатическом поле, равна нулю), то есть
E + Eинд = 0 или E = Eинд .
Следовательно |
|
|
|
|
|
|||
2k |
Q |
cosα = |
|
|
σ инд |
|
|
. |
|
|
|
||||||
|
|
|||||||
|
|
|
|
|
|
|||
|
r2 |
|
ε0 |
|||||
Откуда получаем |
|
|
|
|
|
|||
σ инд = 2kε0 rQ2 cosα .
Подставим в полученную формулу значения k = 4πε1 0 , cosα = hr , r = 
 R2 + h2 ,
R2 + h2 ,
получим
σ инд = 2 |
1 |
|
ε0 |
Qh |
|
= |
Qh |
|
. |
4πε |
|
|
3 |
|
3 |
||||
|
0 |
|
( R2 + h2 )2 |
|
2π ( R2 + h2 )2 |
||||
Проверим наименование поверхностной плотности зарядов в системе СИ
52

наимен. σ инд = Клм3× м = Клм2 .
Найдем численное значение поверхностной плотности индуцированных зарядов
|
25,0 ×10−9 |
3,00 ×10−2 |
|
σ инд = |
|
|
= 1,91×10−7 Кл/м2. |
|
3 |
||
2× 3,14éêë(8,00 ×10−2 )2 + (3,00 ×10−2 )2 ùúû2
2.Потенциал электростатического поля в центре кольца, согласно принципу суперпозиции, равен алгебраической сумме потенциалов полей, созданных заря-
женным кольцом и его изображением
ϕ= ϕ к + ϕ изобр.к .
Элемент длины dl кольца с зарядом dQ создает поле, потенциал которого в центре
кольца можно рассчитать по формуле
|
|
|
|
|
|
|
|
|
|
|
dϕ |
к = κ |
dQ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Чтобы найти потенциал от всего кольца, возьмем интеграл по его заряду |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
ϕ к = òdϕ к = òk |
dQ |
|
= |
|
k |
òdQ = |
k |
Q . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
Q |
|
|
|
|
|
|
Q |
|
|
|
|
R |
|
|
|
R Q |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
||||||||
Потенциал изображения кольца находится аналогично, только расстояние от |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, а его заряд –Q |
|
|
|
|
|
|||||||||||||||||||||||||||
изображения до центра кольца будет |
|
|
4h2 + R2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ϕ изобр.к = òϕ изобр.к |
= òk |
|
|
|
-dQ |
|
|
|
= - |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
òdQ = - |
|
|
|
|
k |
|
|
Q . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
4h |
2 |
+ R |
2 |
|
|
|
4h |
2 |
+ |
R |
2 |
|
|
|
4h |
2 |
+ R |
2 |
|
||||||||||||||||||||||||||
Q |
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
||||||||||||||||||||||
Таким образом, искомый потенциал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ϕ = |
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
æ |
1 |
|
|
|
|
|
1 |
|
ö |
|
|
|
|
|
|
|
|
|||||||||||
|
|
Q - |
|
|
|
|
|
|
|
|
|
|
|
Q = kQç |
|
|
- |
|
|
|
|
|
|
|
|
÷. |
|
|
|
|
|
|
|
|||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4h2 + R2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
4h2 + R2 |
è |
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Проверим наименование потенциала в системе СИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
наимен. ϕ= Н × м2 × Кл |
= |
Дж |
|
|
= В . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кл2 × м |
|
|
Кл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Подставим числовые значения величин и произведем вычисления |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
æ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
||
ϕ = 8,99 ×10925,0 ×10−9 ç |
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
= 562 В. |
|||||
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
2 |
|
|
|
|
|
|
|
|
−2 2 |
|||||||||||||||
|
ç |
|
|
|
|
|
|
|
|
4( 3,00×10 |
) |
+ |
( 8,00 ×10 |
÷ |
|
|
|
|
||||||||||||||||||||||||||||
|
è 8,00 ×10 |
|
|
|
|
|
|
) |
|
|
ø |
|
|
|
|
|||||||||||||||||||||||||||||||
Ответ: поверхностная плотность индуцированного заряда на проводящей пла- стине σ инд = 1,91×10−7 Кл/м2, потенциал поля в центре кольца ϕ = 562 В.
ЗАДАЧИ
241. Точечный заряд q = 0,15 мкКл находится в центре сферической прово- дящей оболочки. Внешний радиус оболочки R1 = 25,0 см, внутренний R2 = 20,0 см. Определить напряженность электростатического поля Е в точках, удаленных
53

от заряда на расстояние r1 = 50,0 cм и r2 = 10,0 см, а также разность потенциалов ϕ между этими точками.
242. Вне изолированной металлической незаряженной сферы на расстоянии r = 15,0 см от её центра находится точечный заряд q = 20,0 нКл. Каков потенциал ϕ сферы, если её радиус R = 5,00 см?
243. Точечный заряд q = 3,00·10–8 Кл находится на расстоянии а = 3,00 см от большой тонкой металлической пластины. Определить поверхностную плотность зарядов σ инд, индуцированных на пластине в точке, находящейся на расстоянии r1 = 5.00 см от заряда. Воспользоваться методом зеркальных изображений.
244. Две одинаковые металлические пластины размерами 20,0 х 20,0 см на- ходятся на расстоянии d = 1,00 см друг от друга. На одной из пластин находится заряд Q1 = 12,0 нКл, на другой – Q2 = 4,00 нКл. Как распределятся заряды по каж- дой из пластин? Найти разность потенциалов ϕ между пластинами.
245. Два точечных заряда q1 = 1,00 нКл и q2 = –1,00 нКл, расположены на расстоянии l = 5,00 см друг от друга и на одинаковом расстоянии а = 2,50 см от безграничной проводящей плоскости. Применяя метод зеркальных изображений, найти модуль кулоновской силы, действующий на каждый заряд.
246. Тонкое кольцо, равномерно заряженное зарядом Q = 2,00 10–8 Кл, и про- водящая сфера расположены так, что центр сферы находится на оси кольца на расстоянии l = 10,0 см от его плоскости. Радиус кольца R = 2,00 см. Определить потенциал ϕ сферы. Воспользоваться формулой для вычисления потенциала за-
ряженного кольца в точке, лежащей на его оси на расстоянии l от центра
ϕ = Q/(4πεо 
 l2 + R2 ).
l2 + R2 ).
247. Большая металлическая пластина расположена в вертикальной плоско- сти и соединена с землей. На расстоянии а = 10,0 см от пластины находится не- подвижная точка, к которой на нити длиной l = 12,0 см подвешен маленький ша- рик. При сообщении шарику заряда q он притянулся к пластине, в результате чего нить отклонилась от вертикали на угол α = 300. С помощью метода зеркальных изображений, найти заряд шарика q, если его масса m = 0,10 г.
248. Металлический шар, радиус которого R1 = 10,0 см, заряжен до потен- циала ϕ 1 = 300 В. Определить потенциал ϕ 2 этого шара в двух случаях: 1) после того как его окружат сферической проводящей оболочкой радиусом R2 = 15,0 см и на короткое время соединят с ней проводником; 2) если его окружить сфериче- ской проводящей заземленной оболочкой радиусом R2 = 15,0 см.
249. На расстоянии а = 10,0 см от бесконечной проводящей плоскости нахо- дится точечный заряд q = 20,0 нКл. Используя метод зеркальных изображений, вычислить напряженность Е электростатического поля в точке, удаленной от плоскости на расстояние а и от заряда q на расстояние 2а.
54

250. Из трех концентрических очень тонких металлических сфер с радиусами R1 = 1,00 см, R2 = 3,00 см, и R3 = 5,00 см крайние заземлены, а средней сфере со- общен заряд Q = 10,0 мкКл. Определить напряженность Е электростатического поля в точках, находящихся на расстояниях r1 = 0,50 см, r2 = 2,00см, r3 = 4,00 см и r4 = 6,00 см от центра сфер.
Рабочая программа Тема 15. Поляризация диэлектриков. Поляризационные заряды. Вычис-
ление напряженности и потенциала электростатического поля при наличии диэлектриков
Пример решения задач
Расстояние между обкладками плоского конденсатора l = 5,00 мм, разность по- тенциалов Δϕ = 1,20 кВ. Пространство между обкладками заполнено диэлек- триком с диэлектрической восприимчивостью χ = 1. Определить: 1) напряжен- ность E электростатического поля в диэлектрике, 2) поверхностную плотность
σсвободных зарядов на обкладках конденсатора, 3) поверхностную плотность
σпол поляризационных зарядов на диэлектрике.
Дано |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l = 5,00 мм |
|
|
|
|
|
|
|
σ |
|
|
S |
n |
|||
Δϕ = 1,20 кВ |
+ |
+ |
+ |
+ |
+ |
|
|
||||||||
|
|
|
|
× |
|
||||||||||
|
|
|
|
|
|||||||||||
χ = 1 |
|
– |
– |
– |
– |
– |
|
σ пол |
диэлектрик |
|
|
||||
|
|
|
|
|
|||||||||||
E = ?, σ = ?, |
|
E0 |
E |
пол |
ε |
E , P |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
σ пол = ? |
|
|
|
|
σ пол |
проводник |
|
E = 0 |
|||||||
|
|
+ |
+ |
|
+ |
+ |
+ |
|
|
||||||
|
– |
– |
|
– |
– |
– |
|
|
|
|
|
S |
|||
|
|
|
σ |
|
|
|
|
|
|||||||
Анализ и решение
При внесении диэлектрика во внешнее электрическое поле он поляризуется, то есть в нем происходит смещение электрических зарядов: положительные сме- щаются по полю, отрицательные – против поля. Эти заряды называются поляри- зационными и распределяются по поверхности диэлектрика с плотностью σ пол.
Напряженность поля поляризационных зарядов Eпол направлена против напря- женности внешнего поля E0 и ослабляет его. Результирующее поле внутри ди-
электрика определяется по принципу суперпозиции
Е = E0 + Eпол или Е = E0 − Eпол . |
(1) |
Для количественного описания поляризации однородных и изотропных ди- |
|
электриков пользуются векторной величиной P – поляризованностью, |
которая |
линейно зависит от напряженности поля |
|
P = χε0E или P = ε0 (ε − 1 )E ,
55
здесь χ , ε – диэлектрические восприимчивость и проницаемость диэлектрика.
Результирующее поле E в диэлектрике зависит его от свойств. Поляризаци- онные заряды, возникающие в диэлектрике, могут вызвать перераспределение
свободных зарядов, создающих поле. Потому вводят новую величину D – вектор электрического смещения (электрической индукции)
D = εε0 E = ε0E + P , |
(2) |
который характеризует электростатическое поле, создаваемое свободными заря- дами (то есть в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
При расчете поля в диэлектриках применяют два метода. Первый метод ос- нован на принципе суперпозиции. Сначала рассчитывают поле свободных зарядов
E0 . Затем определяют поле поляризационных зарядов Eпол . Далее по формуле (1)
находят напряженность поля Е в диэлектрике. Таким же образом можно полу- чить выражение и для потенциала ϕ электростатического поля в диэлектрике.
По второму методу сначала по теореме Гаусса для поля в диэлектрике нахо- дят вектор электрического смещения D , затем по формуле (2) определяют на- пряженность Е и далее (если необходимо) из соотношения E = −gradϕ рассчи-
тывают потенциал. Для решения задачи применим оба метода.
Метод суперпозиции. Поле в диэлектрике создается свободными σ зарядами, расположенными на обкладках конденсатора и поляризационными σ пол зарядами, расположенными на двух параллельных обкладкам гранях диэлектрика. Напря- женности электростатического поля таких заряженных систем нетрудно вычис- лить, применив теорему Гаусса (см. пример из Темы 11)
E0 = |
σ |
, Eпол = |
σ пол |
(3) |
ε0 |
. |
|||
|
|
ε0 |
|
|
Поверхностная плотность поляризационных зарядов σ пол в диэлектрике свя- |
||||
зана с поляризованностью и напряженностью поля соотношением |
|
|||
σ пол = P = ε |
(ε − 1 )E |
n |
= ε |
χ E |
n |
, |
(4) |
n 0 |
|
0 |
|
|
|
здесь – Pn и En – проекции векторов P и E на нормаль к поверхности диэлек- трика. В нашем случае En = E. Подставим в уравнение (1) значения напряженно- стей из (3)
Е = |
σ |
− |
σ пол |
ε0 |
, |
||
|
|
ε0 |
азначение σ пол возьмем из (4), получим
Е= σ − ε0χ E .
ε0 ε0
Решая это уравнение относительно σ , найдем |
|
σ = Eε0(1 + χ ). |
(5) |
56
Напряженность электростатического поля в диэлектрике E можно найти из известного соотношения
Δϕ = ò2 Eldl .
1
Для однородного поля ( Е = const), каким является поле плоского конденсатора,
E = |
Δϕ |
, |
(6) |
|
l |
|
|
здесь Δϕ – разность потенциалов на обкладках конденсатора, l – расстояние меж- ду ними. Подставим (6) в (4) и (5), получим
σ пол = |
Δϕ |
ε |
0 |
χ , σ = |
Δϕ |
ε0 (1 + χ ). |
|
|
l |
|
|
|
l |
|
|
Метод Гаусса. По теореме Гаусса для электростатического поля в диэлек- |
|||||||
трике |
r |
r |
|
|
|
n |
|
ò |
|
ò |
|
(7) |
|||
|
|
|
|
|
|||
ФD = !DdS |
|
= = !DndS = åQi |
|||||
S |
|
|
|
|
|
i=1 |
|
находим электрическое смещение. Для этого применим её к бесконечно малому цилиндру с основанием S , пересекающему границу проводник – диэлектрик.
Ось цилиндра ориентирована вдоль вектора E (см. рис.). Поток вектора электри- ческого смещения D через внутреннюю часть цилиндрической поверхности ра- вен нулю, так как внутри проводника Eпр , а значит и Dпр , равна нулю. Поэтому
поток вектора ФD сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра, причем D = Dn, так как
r
D −− n . Согласно теореме Гаусса (7), этот поток равен сумме зарядов охватывае- мых поверхностью, то есть
D S = σΔS .
Откуда следует, что
D = σ .
С другой стороны, согласно (2)
D = εε0E .
Сравнивая эти две формулы, получаем значение напряженности поля в диэлек-
трике
E = |
σ |
. |
|
||
|
ε ε |
|
|
0 |
|
Отсюда |
Δϕ |
|
σ = Eε0ε = |
ε0 (1 + χ ). |
|
|
l |
|
Далее, по формуле (4) находим поверхностную плотность поляризационных заря-
дов в диэлектрике
57
|
σ пол = ε |
|
χ E = ε |
|
χ |
σ |
= ε |
|
χ |
|
1 Δϕ |
ε |
|
(1 + χ ) = Δϕ ε |
|
χ , |
||||||||||
0 |
0 |
|
|
0 |
|
|
|
|
|
0 |
0 |
|||||||||||||||
ε ε |
ε ε l |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
что совпадает с результатами, полученными методом суперпозиции. |
||||||||||||||||||||||||||
Проверим наименование поверхностной плотности зарядов |
|
|
||||||||||||||||||||||||
|
|
|
наимен. σ = |
В Кл2 |
|
= В |
Кл2м |
= |
Кл . |
|
|
|||||||||||||||
|
|
|
м Нм2 |
|
|
|
||||||||||||||||||||
Проведем числовые расчеты |
|
|
|
|
м ВКлм2 |
м2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E = |
1,20×103 |
= 2,40 ×105 В/м, σ = |
1,20 ×103 |
8,85 ×10−12 (1 + 1 ) = 4,25 ×10−6 Кл/м2, |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
5,00 ×10−3 |
|
|
|
|
|
|
|
|
5,00 ×10−3 |
|
|
|
|
|
|
|
|||||||||
|
|
σ пол = |
1.20 ×103 |
8,85×10−121 = 2,12 ×10−6 Кл/м2. |
|
|
||||||||||||||||||||
|
|
5,00 ×10−3 |
|
|
||||||||||||||||||||||
Ответ: поверхностная |
плотность |
|
свободных |
зарядов |
σ = 4,25 ×10−6 Кл/м2, по- |
|||||||||||||||||||||
верхностная плотность поляризационных зарядов σ пол = 2,12×10−6 Кл/м2, напря- женность электростатического поля в диэлектрике E = 2,40 ×105 B/м,
ЗАДАЧИ
251. Одной из обкладок плоского конденсатора площадью S = 0,20 м2 сооб- щили заряд Q = 1,00 10–9 Кл. Другую обкладку заземлили. Расстояние между об- кладками d = 2,00 мм. Между обкладкам, параллельно им, поместили две пла- стинки: стеклянную толщиной d1 = 0,50 мм и фарфоровую толщиной d2 = 1,50 мм. Определить напряженности электростатического поля Е в стекле и фарфоре, а также поверхностные плотности поляризационных зарядов σ поляр на этих диэлек- триках.
252. Две концентрические металлические сферы с радиусами R1 = 4,00 см и R2 = 10,0 см имеют соответственно заряды Q1 = – 2,00 нКл и Q2 = 3,00 нКл. Про- странство между сферами заполнено парафином (ε = 3). Определить потенциал электростатического поля ϕ на расстояниях r1 = 2,00 см, r2 = 6.00 см, r3 = 20,0см
от центра сфер. Задачу решить, не применяя формулу связи напряженности с из- менением потенциала.
253. На пластины плоского конденсатора подана разность потенциалов ϕ = 1,00·103 В. Пространство между пластинами заполняется диэлектриком
(ε = 7). Найти напряженность электростатического поля Е в диэлектрике и по- верхностную плотность поляризационных зарядов σ поляр на нем, если при запол- нении конденсатор не отключался от источника напряжения. Расстояние между пластинами d = 3,00 см.
254. В однородное электростатическое поле напряженностью Е0 = 700 В/м
перпендикулярно полю помещается бесконечная плоскопараллельная стеклянная пластина (ε = 7). Определить: 1) напряженность электростатического поля Е и
58
электрическое смещение D внутри пластины; 2) поляризованность |
Р стекла; |
3) поверхностную плотность поляризационных зарядов σ поляр на стекле. |
|
255. На пластины плоского конденсатора, расстояние между |
которыми |
d = 3,00 см, подана разность потенциалов ϕ = 1,00 кВ. Пространство между пла-
стинами заполняется диэлектриком (ε = 7). Найти напряженность электростатиче- ского поля Е в диэлектрике и поверхностную плотность поляризационных заря- дов σ поляр. При заполнении конденсатор был отключен от источника напряжения.
256. Пространство между пластинами плоского конденсатора заполнено па- рафином (ε = 2). Расстояние между пластинами d = 8,85 мм. Какую разность по- тенциалов ϕ необходимо подать на пластины, чтобы поверхностная плотность поляризационных зарядов на парафине σ поляр = 0,10 нКл/см2?
257. Расстояние между пластинами плоского конденсатора d = 5,00 мм. По- сле зарядки конденсатора до разности потенциалов ϕ = 500 В между пластина-
ми вдвинули стеклянную пластинку (ε = 7). Определить диэлектрическую вос- приимчивость стекла χ и поверхностную плотность поляризационных зарядов σ поляр на его поверхности.
258. Плоский конденсатор, между обкладками которого помещена стеклян- ная пластинка (ε = 6) толщиной d = 2,00 мм, заряжен до разности потенциалов ϕ = 200 В. Пренебрегая величиной зазора между пластинкой и обкладками, найти напряженность Е электростатического поля в стекле, поверхностную плот- ность поляризационных зарядов на стекле σ поляр, а также поверхностную плот-
ность свободных зарядов σ на обкладках конденсатора.
259. Пространство между обкладками плоского конденсатора заполнено ди- электриком. Расстояние между обкладками d = 2,00 мм, разность потенциалов ϕ 1 = 600 В. Если, отключив источник напряжения, вынуть диэлектрик из кон- денсатора, то разность потенциалов возрастет до ϕ 2 = 1,80 кВ. Найти поверхно-
стную плотность поляризационных зарядов σ поляр на диэлектрике.
260. Между обкладками плоского конденсатора приложена разность потен- циалов ϕ = 200 В. Расстояние между ними d = 1,00 см. Определить напряжен-
ность электростатического поля Е и поверхностную плотность поляризационных зарядов σ поляр в эбонитовой пластинке (ε = 3), помещенной на нижнюю обкладку конденсатора. Толщина пластинки d2 = 8,00 мм.
Рабочая программа Тема 16. Энергия и плотность энергии электростатического поля
Пример решения задач
Найти энергию W уединённой сферы, радиусом R = 4,00 см заряженной до по- тенциала φ =500 В.
59
Дано |
Анализ и решение |
|
R = 4,00 см |
Электростатическое поле, создаваемое заряженной сфе- |
|
φ =500 В |
рой, существует как внутри сферы, так и вне её. Это поле яв- |
|
|
ляется неоднородным, и его энергия распределяется в про- |
|
W = ? |
||
странстве неравномерно. Однако, объемная плотность энер- |
||
|
гии будет одинакова во всех точках, отстоящих на равных расстояниях от центра сферы, так как поле заряженной сферы обладает сферической симметрией. Пол-
ная энергия поля выражается интегралом
W = òωdV ,
V
где dV – элементарный объем, ω – объемная плотность энергии электростатиче- ского поля, определяемая формулой
|
|
|
|
|
|
|
ω = |
1 |
ε |
|
E2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, решение данной задачи сводится к нахождению напряженно- |
|||||||||||||||||
сти поля, созданного заряженной сферой. |
|
|
|
|
|
|
|
||||||||||
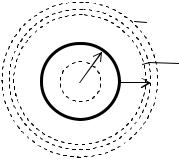
|
|
|
|
|
|
Идеальная сферическая |
симметрия позволяет |
||||||||||
|
|
|
|
|
найти напряженность с помощью теоремы Гаусса: |
||||||||||||
|
|
|
S2 |
|
|
|
|
r |
r |
|
|
r |
r |
|
1 |
n |
|
ϕ |
|
|
ФE |
= !EdS |
=!EdS cos(E ^ dS) = !EndS = |
åQi , |
|||||||||||
|
|
||||||||||||||||
|
|
|
|
|
ò |
|
|
|
|
ò |
|
|
ò |
ε0 |
i=1 |
||
S |
R |
dr |
|
|
S |
|
|
|
|
S |
|
|
S |
||||
R |
|
где S – площадь вспомогательной поверхности, кото- |
|||||||||||||||
S11O |
|
|
r |
|
рой следует придать форму сферы, концентричной |
||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
рассматриваемой сфере. Для расчета напряженности |
||||||||||||
|
|
|
|
|
проведем вспомогательные поверхности S1 и S2 (см. |
||||||||||||
|
|
|
|
|
рисунок). Так как заряд сферы положительный, то во |
||||||||||||
всех точках каждой из этих поверхностей ( E ^ dS ) = 0 и Е = const. Тогда |
|
|
|||||||||||||||
|
|
|
|
|
ò |
EdS = |
ò |
EdS =E4π r2 , |
|
|
|
|
|
||||
|
|
|
|
|
! |
! |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
S1,2 |
|
|
S1,2 |
|
|
|
|
|
|
|
|
|
где r – радиус вспомогательной поверхности.
При r < R сумма зарядов, охваченных поверхностью S1
n
åQi = 0 ,
i=1
так как внутри сферы зарядов нет. Следовательно,
n
E4π r2 = åQi = 0.
i=1
Таким образом, внутри сферы напряженность поля E, его объемная плотность энергии ω и сама энергия W равны нулю.
При r > R сумма зарядов, охваченных поверхностью S2
n
åQi = Q ,
i=1
60
