ZO-2008
.pdfТаким образом, момент инерции стержня, у которого ось вращения проходит через один из его концов, равен
J |
c |
= |
1 |
m |
l2 . |
(4) |
|
||||||
|
|
3 c |
|
|
||
Момент инерции диска определим с помощью теоремы Штейнера. Эта тео-
рема сводит вычисление момента инерции тела относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс
Jд = J0 + mдa2 , |
(6) |
здесь Jд – момент инерции диска относительно заданной оси, J0 – момент инерции диска, относительно оси, проходящей через его центр масс параллельно заданной, а – расстояние между осями. Величину J0 вычислим по формуле (2), в которой элемент массы определяется выражением (3), а r измеряется расстоянием от эле- мента массы диска до оси, проходящей через его центр. Площадь элемента массы
диска dmд определим по формуле
dS = dl × dr = rdα × dr , |
(7) |
где dl – длина элемента, равная длине дуги, радиус которой r, dr – его ширина, dα – центральный угол дуги. Подставляем в интеграл (2) массу элемента диска
(3) с учетом выражения (7). Пределы интегрирования определяются радиусом диска R и углом α = 2π
J0 = òR |
mд |
r3dr2òπ dα = |
mд |
|
R4 |
2π = |
1 |
mд R2 . |
||
2 |
2 |
4 |
2 |
|||||||
0 π R |
0 |
π R |
|
|
||||||
Полученное выражение подставляем в (6) |
|
|
|
|
|
|||||
|
Jд = |
1 |
mдR2 + mд( l + R )2 , |
|
|
|||||
|
2 |
|
|
|||||||
где ( l + R ) = a – расстояние между осями.
(8)
(9)
Найденные выражения момента инерции стержня (4) и момента инерции диска (9) подставляем в формулу (1)
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
2 |
|
2 |
|
|
|
||
|
|
|
J = |
|
|
|
mcl |
|
+ |
|
mдR |
|
+ mд( l |
+ R ) . |
|
|
|
|||
|
|
|
|
3 |
|
2 |
|
|
|
|
||||||||||
Заменяем величины их числовыми значениями, получаем |
|
|
|
|||||||||||||||||
1 |
|
2 |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
||
J = |
|
0,10 ×1,00 |
|
+ |
|
0,50 × 0,25 |
|
+ 0,50(1,00 |
+ 0,25 ) |
= 0,83 кг×м |
. |
|||||||||
3 |
|
2 |
|
|||||||||||||||||
Ответ: момент инерции физического маятника |
относительно |
заданной оси |
||||||||||||||||||
J = 0,83кг×м2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ЗАДАЧИ
141. Найти момент инерции J тонкого однородного кольца массой m =100 г и радиусом R =20,0 см относительно оси, лежащей в плоскости кольца и проходя- щей через его центр.
21
142. Вывести формулу и рассчитать момент инерции J плоской однородной прямоугольной пластины массой m = 800 г относительно оси, совпадающей с од- ной из ее сторон, если длина другой стороны b = 40,0 см.
143. Определить момент инерции J цилиндрической муфты относительно оси, совпадающей с ее осью симметрии, если она имеет массу m = 0,20 кг, внут- ренний радиус R1 = 3,00 см, внешний R2 = 5,00 см.
144. Определить момент инерции J кольца массой m = 50,0 г и радиусом R = 10,0 см относительно оси, касательной к кольцу.
145. Диаметр диска D = 20,0 см, масса m = 800 г. Определить момент инер- ции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.
146. Цилиндр диаметром D = 12,0 см, имеющий массу m = 3,00 кг, лежит бо- ковой поверхностью на горизонтальной плоскости. Определить момент инерции J цилиндра относительно оси, проходящей по линии касания его с плоскостью.
147. Вывести формулу и рассчитать момент инерции J однородной прямо- угольной пластинки относительно оси, перпендикулярной к пластинке и прохо- дящей через одну из ее вершин. Масса пластинки m = 0,20 кг, длинна a = 20,0 см и ширина b = 10,0 см.
148. Однородный диск радиусом R = 20,0 см имеет вырез в виде круга радиу- сом r = R/2. Центр выреза смещен относительно центра диска на расстояние R/2. Масса оставшейся части диска m1 = 7,30 кг. Найти момент инерции J такого диска
относительно оси перпендикулярной к плоскости диска и проходящей через его центр. Воспользоваться формулой момента инерции диска относительно оси про- ходящей через его центр.
149. Определить момент инерции J равностороннего проволочного треуголь- ника со стороной a = 10,0 см относительно оси, совпадающей с одной из сторон треугольника. Масса треугольника m = 12,0 г и равномерно распределена по дли- не проволоки.
150. Пустотелый цилиндр с тонкими стенками лежит на горизонтальной плоскости. Масса цилиндра m = 1,50 кг, радиус R = 20,0 см. Найти момент инер- ции J цилиндра относительно оси, проходящей по линии касания его с плоско- стью.
Рабочая программа Тема 6. Вращение твердого тела вокруг неподвижной оси. Момент силы.
Уравнение динамики вращательного движения твердого тела
Пример решения задач
Через блок массой m =1,00 кг перекинута нить, которая с одной стороны соеди- нена с грузом, находящимся на наклонной плоскости, а с другой с грузом, висящим вертикально. Масса первого тела m1 = 0,20 кг, масса второго тела m2 = 0,30 кг,
22
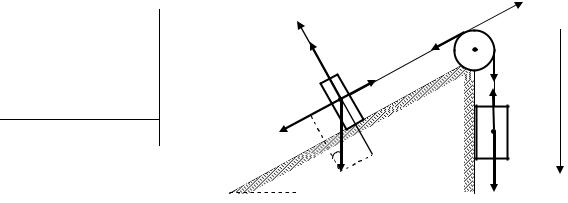
угол наклона плоскости к горизонту равен α = 30°. Коэффициент трения перво- го тела с плоскостью μ = 0,02. Определить разность сил натяжения Fнат по
обе стороны от блока. Блок считать однородным диском, а нить невесомой и нерастяжимой.
Дано
m = 1,00 кг m1 = 0,20 кг
m2 = 0,30 кг α = 30о
μ = 0,02
Fнат = ?
Х
У
Fн2
N1 Fн1
m1 g sinα
F т р |
m1 gcosα |
|
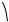α αm1 g
Z |
F* |
|
|
|
н2 |
|
Fн2 |
|
У |
|
m2 g |
Анализ и решение
Заданная система состоит из трех тел – грузов m1 и m2 и блока m. Груз m1 на- ходится под действием четырех сил: силы тяжести m1 g , силы натяжения нити
Fнат1 , силы нормальной реакции наклонной плоскости N и силы трения Fтр . На
второй груз действуют сила тяжести m2 g и сила натяжения нити Fнат 2 . Так как масса блока соизмерима с массой грузов, то силы, с которыми нить действует на
грузы, не равны между собой. |
|
|
Запишем для грузов второй закон Ньютона |
r |
|
r |
, |
|
Fнат1 + N + m1 g + Fтр |
= m1a1 |
|
r |
r |
|
Fнат2 + m2 g = m2a2 . |
|
|
Введем для описания движения тела m1 оси координат Х и У, тела m2 – ось У и заменим векторные уравнения скалярными, связывающими между собой проек-
ции сил и ускорений на эти оси
Fнат1 -Fтр -m1 gsina=m1a1, |
(1) |
N-m1gcosб=0 , |
(2) |
m2 g-Fнат2 =m2a2 . |
(3) |
Блок вращается вокруг неподвижной горизонтальной оси Z, проходящей че- рез его центр, следовательно, моменты сил тяжести блока и реакции оси равны нулю. Считаем, что нить не скользит относительно блока, поэтому вращение бло-
ка вызывается действием только сил натяжения нити F*нат1 и F нат2 . Тогда основ-
ное уравнение динамики вращательного движения для блока
Mz2 -Mz1 =Jеz или ( F* нат2 R- F нат1 R) = Jεz , |
(4) |
23
где Mz1 , Mz2 , J , εz = aRτ – моменты сил натяжения, момент инерции блока отно-
сительно оси Z, проекция вектора его углового ускорения на эту ось. Так как нить
невесома, то Fнат1 = F нат1 и Fнат2 = F нат2 . Поскольку нить не проскальзывает от- носительно блока, то касательное ускорение aτ его точек, соприкасающихся с ни-
тью, равно ускорению нити в любой ее точке, а следовательно, и ускорению гру-
зов
aτ = a1 = a2 .
Учитывая это, преобразуем уравнение (4) |
|
|
aτ |
|
|
|
|
||
( F |
− F |
|
)R = J |
. |
|
|
|
||
|
|
|
|
|
|||||
нат 2 |
нат1 |
|
R |
|
|
|
|||
Выразим силу трения |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Fтр = μN1 = μm1 gcosα , |
|
|
|
||||||
и учитывая, что момент инерции однородного диска J = |
1 |
mR2 |
, получаем систе- |
||||||
2 |
|||||||||
му уравнений |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
F1нат - μm1gcosα - m1 gsinα = m1aτ , |
(5) |
||||||||
m2 g - Fнат2 = m2aτ , |
|
|
(6) |
||||||
F = |
1 |
ma . |
|
|
(7) |
||||
2 |
|
|
|||||||
|
нат |
τ |
|
|
|
||||
Из уравнения (7) находим ускорение aτ , подставляем его в уравнения (5) и (6) и
решаем их относительно величины |
Fнат . Получаем |
|
||||||||||||
|
|
|
|
mg |
|
|
|
é |
ù |
|
||||
|
|
Fнат = 2(m + m |
|
) |
|
|
||||||||
|
|
2 |
+ m ëm2 |
- m1 (μ cosα + sinα )û . |
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||
Проверим наименование силы в системе СИ |
|
кг × м |
|
|
||||||||||
|
|
|
наимен. |
F = |
|
кг = Н . |
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
нат |
|
с2 × кг |
|
|||
Подставим числовые значения величин и произведём вычисления |
|
|||||||||||||
Fнат = |
|
1,00 ×10,0 |
|
× |
é0,30 - 0,20(0,02cos300 + sin300 )ù |
= 0,98Н. |
||||||||
2 |
(0,20 + 0,30) + |
1,00 |
||||||||||||
|
|
|
ë |
|
|
û |
|
|||||||
Ответ: разность сил натяжения |
|
|
Fнат = 0,98 Н. |
|
||||||||||
ЗАДАЧИ
151. На горизонтальную неподвижную ось насажен блок, представляющий собой сплошной цилиндр массой M = 50,0 кг. Через него перекинута невесомая веревка, на концах которой висят две обезьяны массой m = 40,0 кг каждая. Первая обезьяна начинает подниматься с ускорением a1 = 2,00 м/c2 относительно веревки.
24
Определить, с каким ускорением a2 относительно неподвижной системы коорди- нат будет двигаться вторая обезьяна.
152. Найти ускорение а центра масс однородного шара массой m = 1,00 кг, скатывающегося без скольжения по плоскости, которая образует угол α = 300 с горизонтом. Чему равна сила трения Fтр между шаром и плоскостью?
153. По наклонной плоскости скатывается без скольжения сплошной одно- родный цилиндр. Угол наклона плоскости к горизонту α = 300, масса цилиндра m = 300 г. Найти силу трения Fтр между цилиндром и плоскостью.
154. На шероховатой доске на расстоянии l = 0,50 м от ее правого конца ле- жит сплошной цилиндр. Доску начинают двигать с ускорением а0 = 1,00 м/с2 вле- во. С какой скоростью относительно доски будет двигаться центр цилиндра в тот момент, когда он будет находиться над краем доски? Движение цилиндра относи- тельно доски происходит без скольжения.
155. По горизонтальному столу может катиться баз скольжения сплошной цилиндр массой m = 800 г. На цилиндр намотана нить, к свободному концу кото- рой, переброшенному через легкий блок, подвешен груз такой же массы. Система предоставлена сама себе. Найти ускорение а груза и силу трения Fтр между ци- линдром и столом.
156. К краю стола прикреплен блок. Через блок перекинута невесомая и не- растяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, другой по вертикали вниз. Ускорение грузов a = 3,14 м/с2, а их массы равны массе блока m1 = m2 = m. Определить коэффициент трения μ между
поверхностями груза и стола.
157. К концам легкой и нерастяжимой нити, перекинутой через блок, подве- шены грузы массами m1 = 0,20 кг и m2 = 0,30 кг. Во сколько раз отличаются силы, действующие на нить по обе стороны от блока, если масса блока M = 0,40 кг? Си- лами трения и проскальзывания нити по блоку пренебречь.
158. Блок в виде однородного диска массой M = 1,00 кг укреплен на конце стола. Через блок перекинута нить, к концам которой прикреплены грузы. Один из грузов движется по столу, а другой – вдоль вертикали вниз. Коэффициент тре- ния груза о стол μ = 0,10. Найти силы натяжения Fнат нитей и ускорение a, с ко- торым движутся грузы, если их массы m1 = m2 = 1,00 кг.
159. Сплошному однородному шару радиусом R = 0,10 м, лежащему на гори- зонтальной плоскости, сообщается в начальный момент времени поступательная скорость υ 0 = 0,50 м/с без вращения. Учитывая трение скольжения, но, пренебре- гая трением качения, найти угловую скорость шара ω , когда его движение перей- дет в чистое качение.
25
160. Однородный цилиндр лежит на горизонтальной доске. Доске сообщили ускорение a = 0,50 м/с2 в горизонтальном направлении перпендикулярно оси ци- линдра. Найти ускорение оси цилиндра a0 в отсутствие скольжения.
Рабочая программа Тема 7. Момент импульса относительно неподвижной точки и непод-
вижной оси вращения. Уравнение моментов. Закон сохранения момента импульса для твердого тела
Пример решения задач
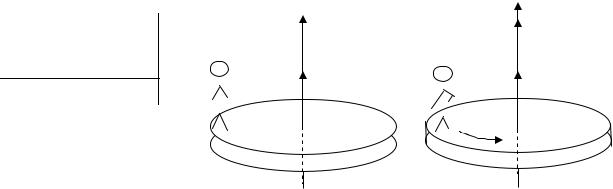
Платформа, в виде диска, может вращаться около вертикальной оси Z, прохо- дящей через её центр. На краю платформы стоит человек массой m = 60,0 кг. На какой угол ϕпл повернется платформа, если человек пойдет вдоль края плат-
формы и, обойдя её, вернется в исходную точку? Масса платформы M = 240 кг.
Дано m = 60,0 кг M = 240 кг
ϕпл = ?
|
|
Z |
|
|
Z |
|
||
|
|
|
|
L2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
ω1 |
|
|
ω2 |
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ и решение
Принимаем платформу за абсолютно твердое тело, а человека – за матери- альную точку. Задачу будем решать в системе отсчета, связанной с Землей. За
время dt человек пройдет по краю платформы угловой путь dϕч = ωчdt ,
здесь ωч – угловая скорость человека относительно платформы. За то же самое
время платформа повернется около своей оси на угол
dϕпл = ωплdt ,
здесь ωпл – угловая скорость платформы относительно Земли. Из сравнения этих уравнений следует, что
dϕпл |
= |
ωпл dϕч . |
(1) |
|
|
ωч |
|
Отношение угловых скоростей ωпл найдем из закона сохранения момента
ωч
импульса системы «человек – платформа». При перемещении человека по плат- форме на систему действуют внешние силы: силы реакции оси Nоси , силы тяже-
26
сти человека и платформы mq , Mq , сила нормальной реакции платформы Nпл .
Суммарный момент этих сил относительно оси Z, равен нулю, следовательно, для нашей системы выполняется закон сохранения момента импульса: в инерциальной системе отсчета момент импульса замкнутой системы сохраняется, то есть
не меняется со временем
N
LcZ = åLZi ( t ) = const .
i=0
Для нашего случая
Lc |
= Lc |
, |
(2) |
Z1 |
Z 2 |
|
|
где LcZ1 ,LcZ 2 – моменты импульса системы относительно оси Z до и после пере-
мещения человека. Так как, до взаимодействия человек и платформа не двига- лись, то проекции их угловых скоростей на ось вращения равны нулю, следова- тельно,
Lc |
= ( J |
ч |
+ J |
пл |
)ω |
z |
= 0 , |
(3) |
Z1 |
|
|
|
|
|
здесь Jч и Jпл – моменты инерции человека и платформы относительно оси вра- щения.
Момент импульса LcZ 2 есть сумма моментов импульса платформы и человека относительно оси вращения
Lc |
= J ω |
+ J |
пл |
( −ω |
пл |
), |
(4) |
Z 2 |
ч ч |
|
|
|
|
здесь ωч , –ωпл – проекции угловых скоростей человека и платформы на ось вра-
щения. Минус обусловлен тем, что угловые скорости платформы и человека про- тивоположны по направлению.
Для нахождения угловой скорости человека следует учесть, что он одновре- менно участвует в двух движениях: перемещается относительно платформы с уг-
ловой скоростью ωч и вращается вместе с ней в противоположную сторону с уг-
ловой скоростью ωпл относительно Земли. Таким образом |
|
ωч = (ωч − ωпл ). |
(5) |
Момент инерции человека, которого мы считаем материальной точкой, отно-
сительно оси вращения
Jч = mR2 , |
(6) |
где R – расстояние от человека до оси вращения, равное радиусу платформы. Мо-
мент инерции платформы
Jпл = |
1 |
МR2 . |
(7) |
|
2 |
||||
Подставим выражение (5) в формулу (4) |
|
|
||
|
|
|
Lc |
= J |
(ω − ω |
пл |
) − J ω |
пл |
, |
(8) |
Z 2 |
ч |
ч |
пл |
|
|
а затем (8) и (3) в (2)
0 = Jчωч − Jчωпл − Jплωпл .
27
Или
Jчωч = ( Jч − Jпл )ωпл .
Откуда получаем
|
|
ωпл |
= |
|
|
Jч |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
ωч |
|
|
|
Jпл + Jч |
|
|
|
|
|
|||||||
После подстановки значений моментов инерции из (6) и (7) |
||||||||||||||||||
|
|
ωпл |
= |
|
|
2m |
|
|
|
|
. |
|
(9) |
|||||
|
|
|
2m + М |
|||||||||||||||
|
|
ωч |
|
|
|
|
|
|
|
|
||||||||
Выражение (9) подставляем в формулу (1) и интегрируем её |
||||||||||||||||||
|
|
ϕпл |
|
2π |
|
2m |
|
|
|
|
|
|
|
|
|
|||
|
|
ò dϕпл = ò |
|
|
|
|
|
|
dϕч . |
|
|
|||||||
|
|
|
2m + |
М |
|
|
|
|||||||||||
В результате получаем |
|
0 |
0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|||
|
|
ϕпл = |
|
|
|
|
|
2π . |
|
|
||||||||
|
|
|
2m + М |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В полученную формулу подставляем числовые значения физических величин |
||||||||||||||||||
ϕпл = |
|
2× 60,0 |
|
|
|
|
2π = |
240 |
π = |
2 |
π (рад). |
|||||||
( 2 |
× 60,0 + 240 ) |
|
3 |
|||||||||||||||
|
360 |
|
|
|||||||||||||||
Ответ: платформа повернётся на угол ϕ = |
2 |
|
π рад. |
|
|
|||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
ЗАДАЧИ
161. На краю круглой горизонтальной платформы радиусом R = 0,40 м стоит человек. Платформа вместе с ним вращается с угловой скоростью ω0 = 25,0 рад/с вокруг вертикальной оси, проходящей через центр тяжести платформы. В некото-
рый момент времени человек начинает идти вдоль края платформы со скоростью υч = 1,80 м/с (по отношению к платформе) в противоположную сторону ее враще- ния. Найти изменившуюся скорость платформы ωч , если ее масса M = 200 кг, а масса человека m = 70,0 кг.
162. Деревянный стержень массой М = 6,00 кг и длиной l = 2,00 м может вращаться в вертикальной плоскости относительно горизонтальной оси, прохо- дящей через один из его концов. В другой конец стержня попадает пуля массой m = 10,0 г, летевшая со скоростью υ = 800 м/с, направленной перпендикулярно стержню и оси, и застревает в нем. Определить кинетическую энергию W к стерж- ня после удара и максимальный угол отклонения α max стержня от вертикали.
163. Маховик, имеющий вид диска радиуса R = 40,0 см и массой M = 48,0 кг, может вращаться вокруг горизонтальной оси. К его цилиндрической поверхности прикреплен шнур, к другому концу которого подвешен груз массой m = 0,20 кг. Груз был приподнят и затем отпущен. Упав свободно с высоты h = 2,00 м, груз
28
натянул шнур и, благодаря этому, привел маховик во вращение. Какую угловую скорость ω * приобрел при этом маховик?
164. Стержень, массой М = 0,70 кг и длиной l = 1,50 м, может свободно вра- щаться вокруг неподвижной горизонтальной оси, проходящей через один из его концов. Под действием силы тяжести, стержень переходит из горизонтального положения в вертикальное. Проходя через вертикальное положение, нижний ко- нец стержня упруго ударяет о тело массой m = 100 г, лежащее на гладком гори- зонтальном столе. Определить скорость тела υ * после удара.
165. Человек стоит на диске, который в начале неподвижен, но может вра- щаться относительно вертикальной оси, проходящей через его центр. Момент инерции диска с человеком I = 48,0 кг×м2. В руках человек держит колесо массой m = 3,00 кг и радиусом R = 0,40 м. Его вертикальная ось расположена на расстоя- нии r = 50,0 см от центра диска. Колесо вращается, делая n = 10,0 об/с. Опреде- лить угловую скорость вращения диска ω *, если человек повернет ось колеса на угол α = 1800.
166. Однородный стержень длиной l = 1,00 м может свободно вращаться во- круг горизонтальной оси, проходящей через один из его концов. В другой конец стержня абсолютно неупруго ударяет пуля массой m = 7,00 г, летящая перпенди- кулярно стержню и его оси. Определить массу М стержня, если в результате по- падания пули он отклонился на угол α = 600. Принять скорость пули υ = 360 м/с.
167. Стержень массой М = 10,0 кг и длиной L =2,00 м, подвешенный за один из его концов, отклонили на угол 900 и отпустили. Около положения равновесия он неупруго соударяется с математическим маятником, ось вращения которого совпадает с осью вращения стержня. Масса маятника m = 0,50 кг, длина l = L. Оп- ределить угловую скорость ω * системы после соударения.
168. Маятник в виде однородного шара, жестко скрепленного с тонким неве- сомым стержнем, может качаться вокруг горизонтальной оси, проходящей через конец стержня. В шар, нормально к его поверхности, ударилась пуля и застряла в нем. Масса пули m = 10,0 г, масса шара М = 10,0 кг, его радиус R = 15,0 см. Длина стержня l = R. На какой угол α отклонился маятник в результате удара пули, если она летела горизонтально со скоростью υ = 800 м/с?
169. На краю неподвижной скамьи Жуковского диаметром D = 0,80 м и мас-
сой М = 6,00 кг стоит человек массой m = 60,0 кг. С какой угловой скоростью ω начнет вращаться скамья, если человек поймает летящий на него мяч? Траектория мяча горизонтальна и проходит на расстоянии r = 0,40 м от оси скамьи. Скорость мяча υ = 5,00 м/с, его масса m1 = 0,50 кг.
170. Найти приращение угловой скорости Δω вращения планеты вокруг соб- ственной оси, происходящее вследствие падения на ее поверхность метеорита массой m = 3·103 кг. Метеорит летел в плоскости экватора планеты со скоростью
29
υ = 15·103 м/с под углом α = 300 к вертикали к ее поверхности. Масса планеты и ее радиус соответственно равны M = 2·1027 кг, R = 72·103 м.
Рабочая программа Тема 8. Идеальный газ. Опытные законы идеального газа. Уравнение
состояния идеального газа (уравнение Клайперона-Менделеева). Барометрическая формула.
Пример решения задач
Зависимость давления воздуха от объема задана уравнением p = ( p0 − αV ) , где
p = 2,00×106 Па, α = 5,00×107 Па/м3. Масса воздуха m = 500 г. Определить мак- |
|||||
0 |
|
|
|
|
|
симальную температуру воздуха Тmax. |
|
||||
Дано |
|
|
|
Анализ и решение |
|
p = ( p0 − αV ) |
|
|
|
|
|
|
Для решения задачи воспользуемся уравнением |
||||
p = 2,00×106 |
Па |
Клайперона-Менделеева, которое устанавливает |
связь |
||
0 |
|
между давлением, объемом и температурой для |
|||
α = 5,00×107 Па/м3 |
|||||
m = 500 г |
|
произвольного равновесного состояния идеального газа |
|||
Тmax = ? |
|
|
m |
|
|
|
рV = M RT , |
(1) |
|||
|
|
||||
здесь m – масса газа, М – его молярная масса, R = 8,31 Дж/(моль·К) – универсаль- ная газовая постоянная. Подставим в это уравнение зависимость давления воздуха
от его объёма
m
( p0 − αV )V = M RT .
В полученной формуле температура является функцией только объёма. Выразим
ее
T = MmRα ( р0V − αV 2 ).
Максимальной температуре воздуха соответствует его максимальный объем Vmax .
Для нахождения этой величины приравняем нулю производную dVdT :
dT Mα
dV = mR ( p0 − 2αVmax ) = 0.
В этом выражении нулю может быть равно только выражение в скобках
( p0 − 2αVmax ) = 0 .
Отсюда находим
Vmax = 2pα0 .
Из уравнения
30