2.6. Операторный метод и передаточная функция

Наиболее распространенным методом описания и анализа элементов и систем управления является операторный метод (метод операционного исчисления). В основе метода лежит преобразование Лапласа

(2.48)

которое устанавливает соответствие между функциями действительной переменной t и функциями комплексной переменной р. Функцию времени x(t), входящую в интеграл Лапласа (2.48), называют оригиналом, а результат интегрирования – функцию Х(р) – изображением функции x(t) по Лапласу.

В табл. 2.1 приведены изображения некоторых простейших функций времени, наиболее часто используемых в расчетах СУ.

Таблица 2.1

Изображения простейших функций времени по Лапласу

Наименование функций
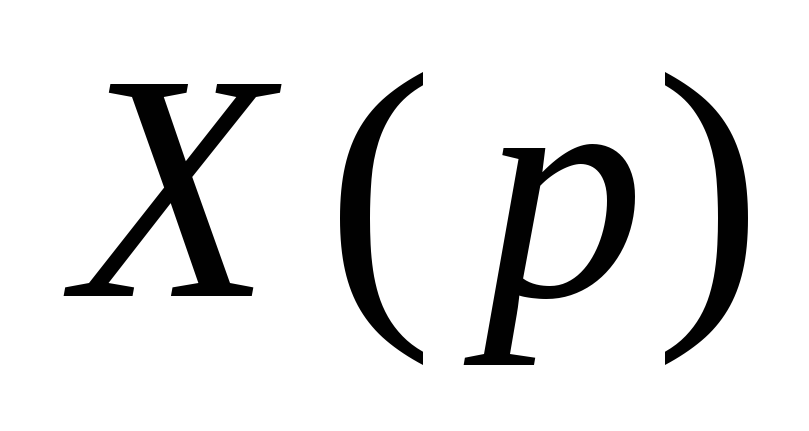
Дельта-функция
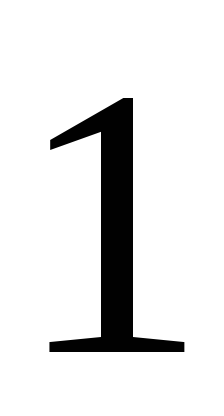
Ступенчатая
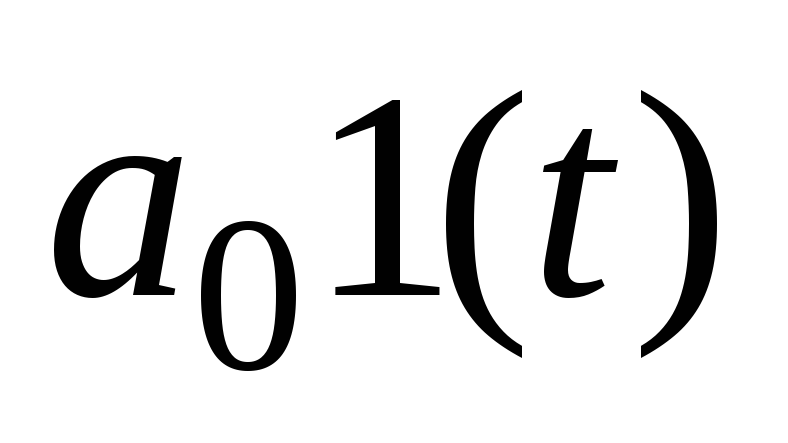
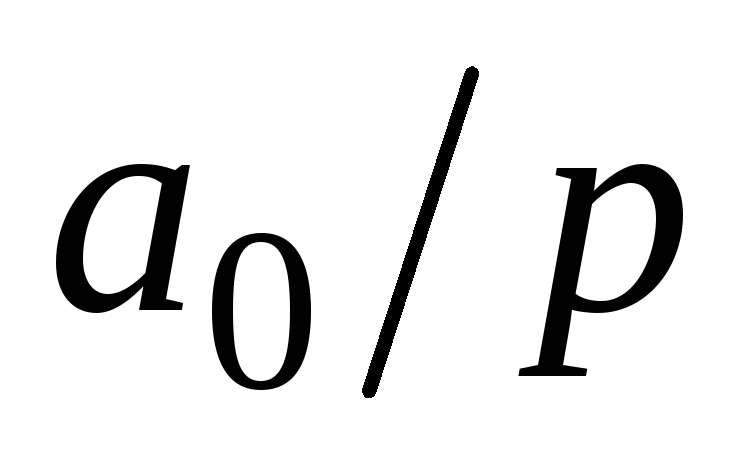
Линейная
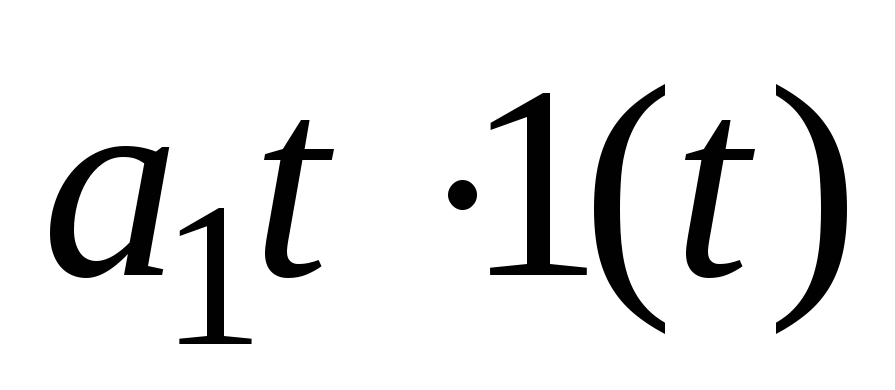
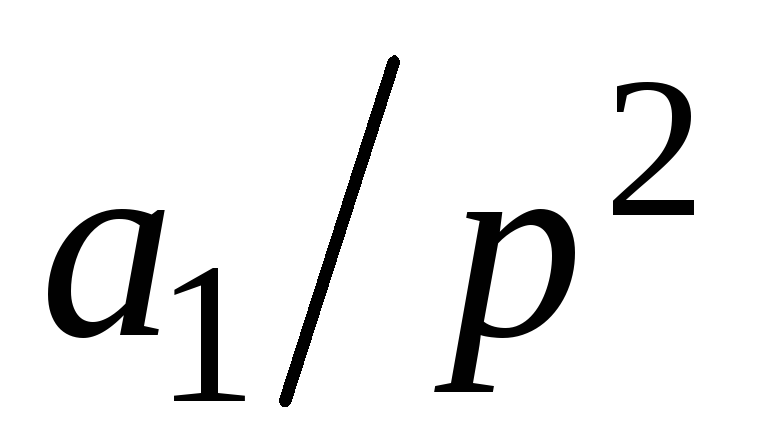
Степенная
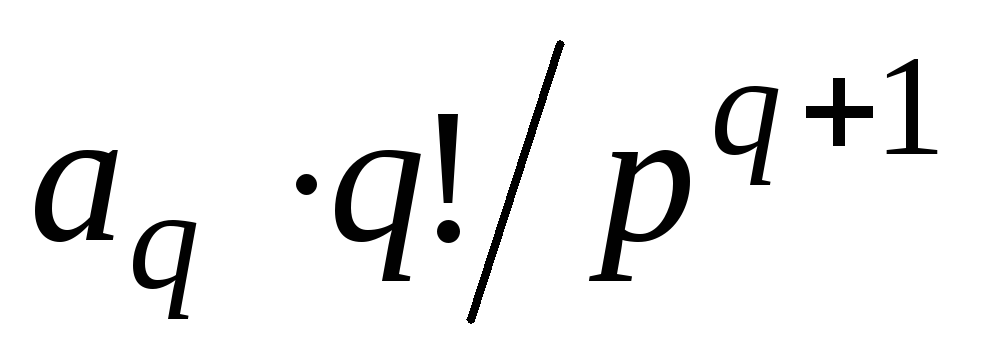
Экспонента

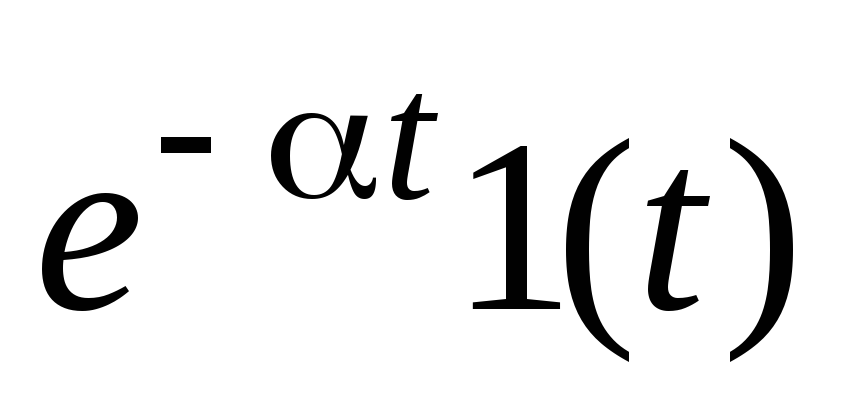
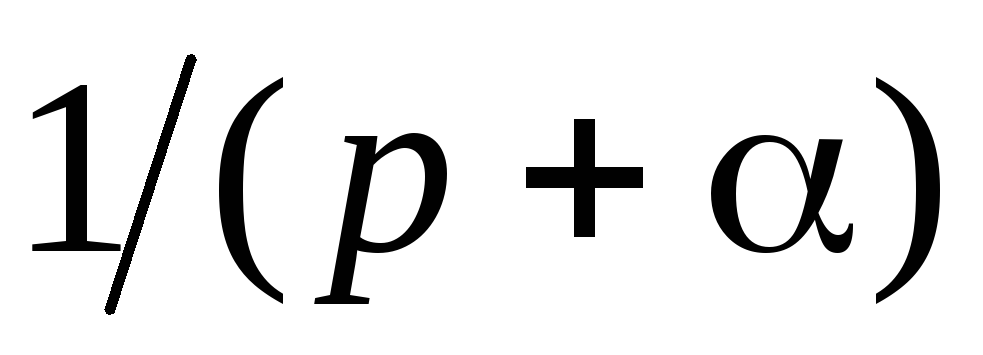
Преобразование Лапласа выполнимо лишь для таких функций времени, которые равны нулю при t<0. Это условие обеспечивается обычно умножением функции x(t) на единичную ступенчатую функцию 1(t). С математической и физической точек зрения такой искусственный прием вполне корректен, так как функции x(t) описывают процессы в СУ, начинающиеся с некоторого момента времени, а этот момент времени всегда может быть принят за начало отсчета.

Некоторые свойства преобразования Лапласа, используемые при анализе автоматических систем, указаны в табл. 2.2.

Таблица 2.2

Некоторые свойства преобразования Лапласа

Наименование	Оригинал	Изображение
Линейность
Правило дифференцирования (при нулевых начальных условия)
Правило интегрирования (при нулевых начальных условия)
Смещение аргумента оригинала (теорема запаздывания)
Теорема о начальном значении оригинала
Теорема о конечном значении оригинала

Широкое распространение операторного метода в теории управления обусловлено тем, что с его помощью определяют так называемую передаточную функцию, которая является компактной формой описания динамических свойств элементов и систем.

Применим преобразование Лапласа к линейному дифференциальному уравнению (2.23), полагая, что до приложения внешнего воздействия система находилась в покое и что все начальные условия равны нулю. Используя свойство линейности и правило дифференцирования (см. табл. 2.2), можно получить алгебраическое уравнение в изображениях

(2.49)

где

Сравнивая уравнение (2.49) с уравнением в символической форме (2.26), можно заметить полную аналогию их структур. Различие уравнений лишь в значении символа p: в первом уравнении он обозначает операцию дифференцирования, во втором – комплексную переменную.

Введем теперь понятие передаточной функции (сокращенно – ПФ). Передаточной функцией W(р) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях

(2.50)

Для системы, описываемой уравнением (2.23), ПФ равна отношению входного оператора K(р) к собственному оператору D(р)

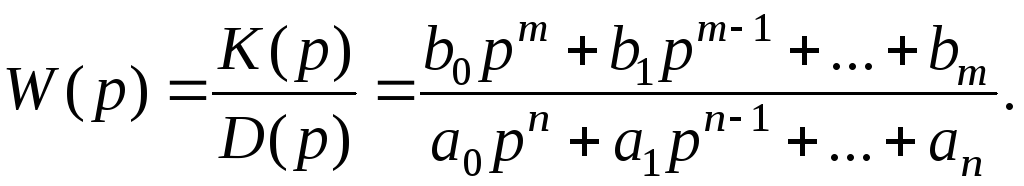(2.51)

Как следует из определений (2.50) и (2.51), ПФ представляет собой некоторый динамический оператор, характеризующий прохождение сигналов через линейный элемент (рис. 2.11,а).

Рис. 2.11. Схемы для определения передаточной функции

электрического четырехполюсника

Передаточную функцию формально можно получить из дифференциального уравнения заменой в нем символа кратного дифференцирования на соответствующую степень р и делением образованного таким образом многочлена правой части уравнения на многочлен левой части.

Передаточную функцию электрических четырехполюсников удобно получить, пользуясь понятием операторного сопротивления. Для этого четырехполюсник необходимо представить в виде схемы делителя напряжения (рис. 2.11,б), состоящей из двух операторных сопротивлений Z₁(р) и Z₂(р). Тогда ПФ между напряжениями u₁ и u₂ может быть определена как отношение выходного сопротивления к входному:

(2.52)

где Z₁(р) и Z₂(р) найдены как эквивалентные операторные сопротивления входного и выходного участков, состоящих из типовых элементов электрических цепей (рис. 2.11,в).

Рассмотрим теперь основные свойства и особенности передаточных функций систем управления и их элементов.

Передаточная функция элемента связана с его импульсной переходной функцией преобразованием Лапласа

(2.53)

соответственно наоборот

(2.54)

Получим в соответствии с теоремами Лапласа о начальном и конечном значениях оригинала (см. табл. 2.2) соотношения, позволяющие по передаточной функции вычислить значения переходной функции h(t) в моменты времени t=0 и t=∞

(2.55)

У реальных элементов систем, описываемых обыкновенными дифференциальными уравнениями вида (2.23), ПФ представляет собой правильную рациональную дробь, у которой степень многочлена числителя меньше или равна степени многочлена знаменателя, т. е. m≤n. Все коэффициенты ПФ – действительные числа, характеризующие параметры элемента (системы).

ПФ является функцией комплексной переменной р=α±jβ, которая может при некоторых значениях переменной р обращаться в нуль или бесконечность. Значение переменной р, при котором функция W(р) обращается в нуль, называют нулем, а значение, при котором обращается в бесконечность, – полюсом передаточной функции. Очевидно, что нулями передаточной функции являются корни полинома К(р), а полюсами – корни полинома D(р). Корни полиномов числителя и знаменателя могут быть комплексными, мнимыми и вещественными числами (в том числе и нулевыми). Если эти корни известны, то ПФ может быть представлена в следующем виде:

(2.56)

где - корни многочленаК(р) (нули ПФ); - корни многочленаD(р) (полюсы ПФ).

Таким образом, каждой конкретной ПФ с заданными коэффициентами соответствует вполне определенное сочетание нулей и полюсов. По распределению нулей и полюсов ПФ на комплексной плоскости с координатами α и jβ можно судить о свойствах элемента или системы.

Если полиномы D(р) и К(р) имеют один или несколько нулевых корней, то ПФ удобно записывать в такой форме, чтобы полюсы и нули были выделены в явном виде. Так, если ПФ имеет в точке р=0 полюс кратности ν, то её удобно записать в виде

(2.57)

где приp→0 стремится к единице.

Передаточная функция (2.56) имеет полюсы в точке p=0, когда один или несколько младших коэффициентов многочлена D(p) равны нулю: Такую передаточную функцию можно представить в виде

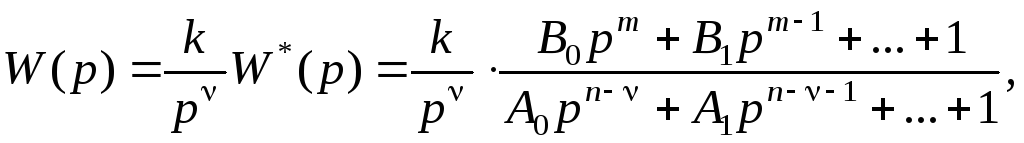(2.58)

где

Величину ν называют порядком астатизма. Коэффициент k имеет размерность

(2.59)

и с некоторой условностью может быть назван передаточным коэффициентом. Условность заключается в том, что понятие «передаточный коэффициент» было введено в качестве характеристики статического режима, а у элементов с ν≠0 статический режим работы не существует.

Если ν =0, то элемент называется статическим, а его передаточная функция при р=0 равна передаточному коэффициенту

(2.60)

Пример 1. Найдем ПФ электрического колебательного контура, который представлен в виде четырехполюсника (рис. 2.11, б), причем входной участок образован последовательным соединением резистора r и индуктивности L, а выходной – из емкости С.

Операторные сопротивления участков: Z₁(p)=r +pL, Z₂(p)=1/pC. Согласно (2.52) ПФ равна

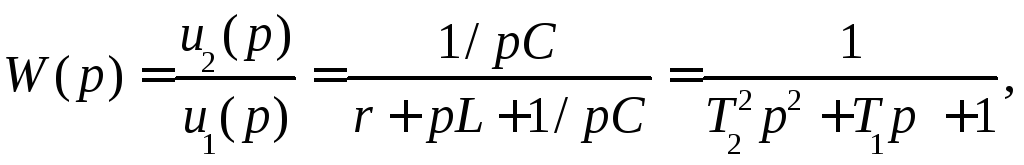(2.61)

где .

Пример 2. Определим ПК системы, описываемой ПФ вида

(2.62)

Запишем формулу (2.62) согласно (2.58)

(2.63)

Откуда ПК