Д15. Условия принадлежности прямой плоскости

При построении прямой, принадлежащей плоскости, следует исходить из условия принадлежности:

Прямая принадлежит плоскости, если она проходит:

1)через две точки, принадлежащие этой плоскости;

2)через одну точку, принадлежащую плоскости, параллельно прямой,

принадлежащей плоскости.
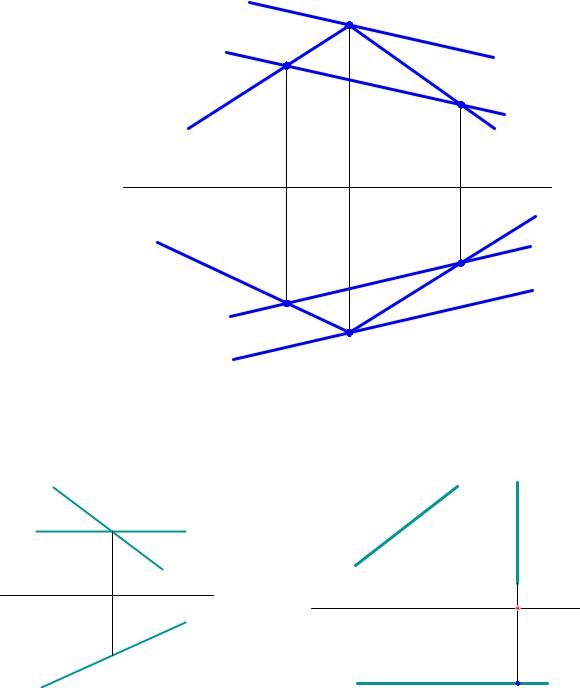
Прямые m и n,	принадлежащие плоскости α(аÇb) показаны на			рис. 48.
Прямая n проходит	через точки1 и 2 плоскости α. Прямая m		принадлежит
плоскости α, так как проходит через точку С и параллельна прямой n плоскости α.
Если прямая принадлежит плоскости частного положения(проециру-
ющей или уровня), то проекция прямой		совпадает с	той	одноименной
проекцией плоскости, которая изображается в виде прямой линии(на основе
собирательного свойства этой проекции плоскости).
Прямые a и h	на рис. 49 принадлежат	горизонтально-проецирующей

плоскости β, так как их горизонтальные проекции а1 и h1 совпадают с β1;

Прямые b и c на рис. 50 принадлежат фронтальной плоскости α, так как их горизонтальные проекции b1 и c1 лежат на α1.

				45
			m2	С
			n2	2
			n2	12	22
		а2			22
		а2				b2
	x					b2
	x
	а1				21	b1
	а1			11	21
			n1	11
			n1
			m1	С
			m1	1
				Рис.48
а2		h2		b2
		h2				c2
х						c2
х
			1	b =a
		h				c
		=
	a1
	=			1	1		1
	1						1
b
	Рис.49				Рис.50
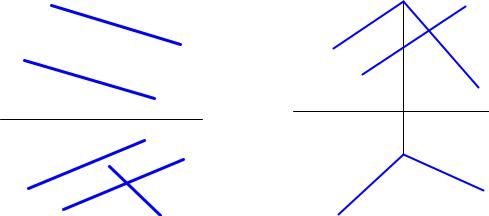
ЗАДАЧА 1. Построить недостающую проекциюn2					прямой n, принадлежащей
плоскости α(а\|\|b) (рис.51).
ЗАДАЧА 2. Построить недостающую проекцию n1 прямой n, принадлежащей
плоскости β(aÇb), если n2\|\|a2 (рис.52).

Д16. Главные линии плоскости

Главные линии плоскости– это прямые, принадлежащие плоскости и занимающие особое положение по отношению к плоскостям проекций. К

главным линиям относятся линии уровня плоскости(горизонталь, фронталь и профильная прямая) и линии наибольшего наклона к плоскостям проекций.

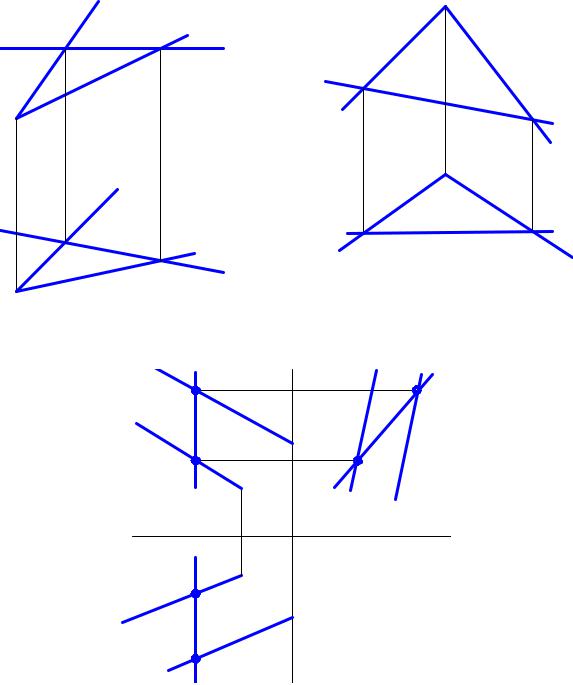
Горизонталь плоскости – это прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций П1 (прямая h на рис. 53).

На чертеже фронтальная проекция h2 || x , а горизонтальная h1 строится по двум точкам, принадлежащим плоскости.

Фронталь плоскости – это прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций П2 (прямая ƒ на рис. 54).

На чертеже горизонтальная проекцияƒ1 || x, а фронтальная проекция ƒ2

стоится по двум точкам, принадлежащим плоскости.

Профильная прямая плоскости – это прямая, принадлежащая плос-

кости и параллельная профильной плоскости проекций П3 (прямая АВ на рис. 55).

			47
На чертеже горизонтальная и фронтальная проекции прямойАВ
перпендикулярны оси х (А2В2^x ; А1В1^x) и проходят через две точки плоскости,
принадлежащие заданным прямым m и n.
a2	b2				c
h2	b2				c
					2
					d2
					f2
a1					c1
h1	b1				f1
	b1				d1
					d1
Рис.53					Рис.54
	А2		m	n	A3
			2	3	m3
	B2			B	m3
		n2		3
		n2
n1	B1
n1
m1		A1
			Рис.55
Линии наибольшего наклона плоскости к плоскостям проекцииэто
прямые, принадлежащие плоскости и перпендикулярные к ее линиям уровня. С

<<< < Предыдущая 1 2 3 4 5 67 / 187 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]