
- •ВВЕДЕНИЕ
- •ОБОЗНАЧЕНИЯ И СИМВОЛИКА
- •Д3. Аксонометрия
- •Д4. Метод Монжа. Точка. Проекции точки
- •Д5. Координаты точки
- •Д6. Прямая общего положения. Принадлежность точки прямой
- •Д7. Прямые уровня. Принадлежность точки прямой
- •Д8. Проецирующие прямые
- •Д9. Прямые различного взаимного расположения
- •Д12. Плоскость общего положения. Принадлежность точки плоскости
- •Д13. Проецирующие плоскости. Принадлежность точки плоскости
- •Д15. Условия принадлежности прямой плоскости
- •Д16. Главные линии плоскости
- •Д17. Поверхность. Образование, задание и изображение на чертеже. Принадлежность точки и линии поверхности
- •Д20. Частные виды поверхностей вращения
- •Раздел II. ПОЗИЦИОННЫЕ ЗАДАЧИ
- •Д23. Сечения кривых поверхностей
- •Д24. Цилиндрические сечения
- •Д25. Конические сечения
- •Д26. Сферические сечения
- •Д27. Сечения многогранников
- •Д28. Пересечение поверхностей
- •Д30. Способ вспомогательных секущих плоскостей
- •Д31. Пересечение соосных поверхностей вращения
- •Д32. Способ концентрических сфер
- •Д33. Теорема Монжа
- •Раздел III. МЕТРИЧЕСКИЕ ЗАДАЧИ.
- •Д36. Способ замены плоскостей проекций
- •КОНТРОЛЬНЫЕ ВОПРОСЫ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
|
|
|
23 |
|
|
|
|
|
|
|
|
S2 |
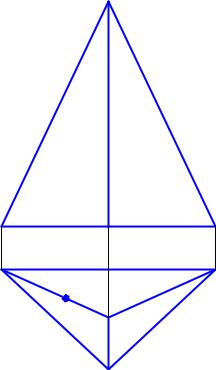
ЗАДАЧА. |
Дана |
пирамида SАВС |
и |
|||
|
|
|
горизонтальная |
|
проекция |
||||
|
|
|
|
точки |
D, |
принадлежащей |
|||
|
|
|
|
ребру АS. Определить, какие |
|||||
|
|
|
|
ребра |
пирамиды |
являются |
|||
|
|
|
|
прямыми общего положения. |
|||||
А |
|
|
|
Построить |
|
|
профильную |
||
2 |
C |
B2 |
проекцию |
|
пирамиды |
и |
|||
|
|
|
|
|
|
||||
|
2 |
фронтальную |
и |
профильную |
|||||
А1 |
|
B1 |
проекции точки D. |
|
|
||||
S1 |
|
|
|
|
|
|
|||
|
|
D1 |
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
Рис.14 |
|
|
|
|
|
|
|
|
|
Д7. Прямые уровня. Принадлежность точки прямой |
|
|
|
||||
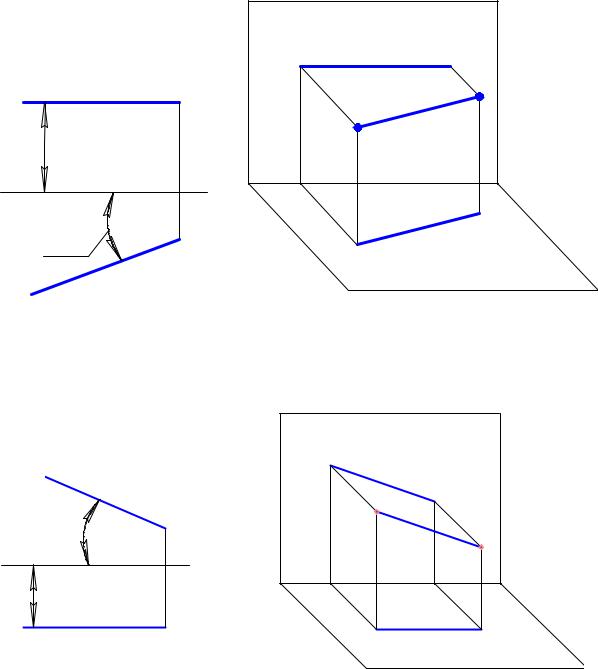
Прямая, параллельная одной из плоскостей проекций, называется прямой
уровня.
Прямая, параллельная горизонтальной плоскости проекцииП1, на-
зывается горизонтальной прямой или горизонталью, параллельная фронтальной плоскости проекции П2 – фронтальной прямой или фронталью, параллельная профильной плоскости проекции П3 – профильной прямой.
Прямая уровня проецируется в натуральную величину на ту плоскость проекций, параллельно которой она расположена, а на две другие плоскости проецируется в виде прямых, параллельных осям проекций.
24
а) |
б) |
p |
h |
|
|
|
2 A |
B |
|
|
|
2 |
2 |
|
|
h2 |
|
h |
2 |
|
|
|
||
|
|
|
|
|
х |
Z=const |
|
А |
|
|
|
h1 |
|
|
|
f |
|
B1 |
|
|
2 |
|
A1 |
|
|
h1 |
|
|
Рис.15
p 1
|
|
p |
|
|
|
|
|
а) |
|
2 |
C |
|
|
|
|
|
б) |
2 |
f 2 |
|
|
|
|
|
|
f2 |
|
|
D2 |
|
|
|
f |
C |
|
|
D |
||
|
|
|
|
|
|||
х |
1 |
|
|
|
f |
|
|
у=const |
|
|
|
|
|||
|
|
|
|
f1 |
|
||
|
f |
|
C1 |
|
|
D1 p |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
1 |
|
Рис.16
|
|
|
|
|
|
25 |
|
|
а) |
В2 |
|
z |
В3 |
б) |
В2 |
В3 |
|
|
|
|
В |
|||||
|
|
х=const |
|
|
||||
|
|
f2 |
f |
|
|
|||
|
А |
|
|
|
1 |
А2 |
|
|
|
|
|
|
|
А |
|
||
х 2 |
|
0 |
|
|
3у |
|
А |
|
|
В1 |
|
|
|
|
|
||
|
|
|
|
|
|
В1 |
3 |
|
|
А1 |
|
у |
|
|
|
А |
|
|
|
|
|
|
|
А1 |
||
|
|
|
|
|
|
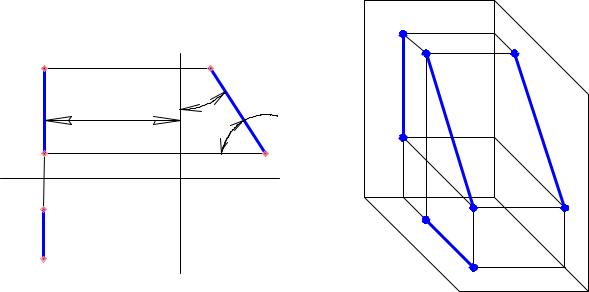
Рис.17 |
|
|
Горизонталь (прямая h на рис. 15). Все точки горизонтали удалены на
одинаковые расстояния от плоскости проекцийП , поэтому фронтальная
1
проекция любой горизонтали параллельна осих (h2 || х). Горизонтальная
проекция горизонтали располагается наклонно к осиx. Величина ее равна
натуральной величине самой горизонтали. Угол j2 между h1 и осью x равен
натуральному углу между горизонталью и плоскостью П2.
Фронталь (прямая f рис. 16). Все точки фронтали удалены на одинаковые
расстояния от плоскости проекций П2, поэтому горизонтальная проекция любой
фронтали параллельна осих (f1 || х). Фронтальная проекция располагается
наклонно к оси х. Величина ее равна натуральной величине самой фронтали.
Угол j1 между f2 и осью x равен натуральному углу между фронталью и плоскостью П1.
Профильная (прямая АВ на рис. 17). Все точки профильной прямой
удалены на одинаковое расстояние от плоскости проекцийП , поэтому
3
горизонтальная проекция любой профильной прямой параллельна осиy (А1В1 || y), а фронтальная – А2В2 || z. Профильная проекция наклонена к осямy и z.
Величина ее равна натуральной величине самой прямой. Угол j1 между А3В3 и
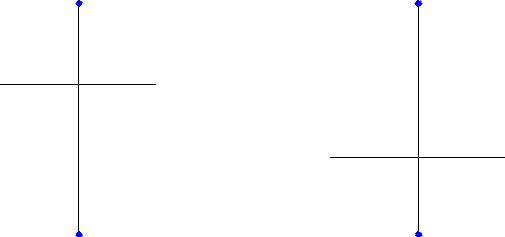
26
осью y равен углу между профильной прямой и плоскостьюП1. Угол j2 между
А3В3 и осью z равен углу между профильной прямой и плоскостью П2.
ЗАДАЧА 1. Построить проекции отрезка АВ, параллельного |
плоскости П1 и |
|
проходящей через точкуА. Натуральная длина отрезка составляет |
||
40 мм. Угол наклона прямой к плоскостиП2 |
равен 45º (рис. 18). |
|
Сколько решений имеет задача? |
|
|
ЗАДАЧА 2. Построить проекции отрезкаСD прямой линии, параллельной |
||
плоскости П2 и проходящей через точкуС. |
Натуральная длина |
|
отрезка составляет 40 мм. Угол наклона прямой |
к плоскостиП1 |
|
равен 30º (рис.19). Сколько решений имеет задача? |
|
|
А2
х
А1
Рис.18
С2
х
С
1
Рис.19
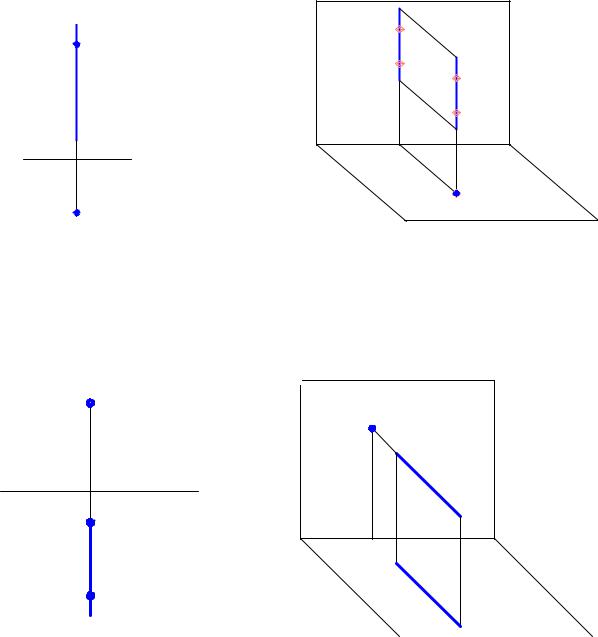
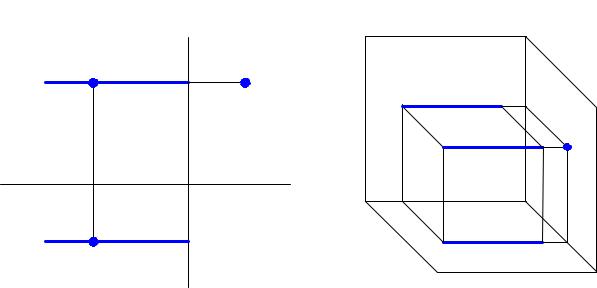
Д8. Проецирующие прямые
Проецирующими называются прямые, перпендикулярные к одной из
плоскостей проекции, т.е. параллельные двум плоскостям проекций.
Прямая, перпендикулярная плоскости П1, называется горизонтально-
проецирующей (прямая a на рис.20); перпендикулярная плоскости П2 – фронтально-
проецирующей (прямая b на рис. 21); перпендикулярная П3 – профильно-
проецирующей (прямая с на рис. 22).
а)
А2
a2


 N2
N2
х
a1=(N1)=A1
а) |
b =(B )=А |
||
|
2 |
2 |
1 |
х |
|
|
|
|
b1 |
B1 |
|
|
А |
|
|
|
|
1 |
|
27
б)
p2 A2 |
|
а2 |
A |
N |
|
2 |
а |
|
|
x |
N |
pа =N =A |
|||
1 |
1 |
1 |
1 |
Рис.20
б)
p |
b2=А2=В2 |
2 |
|
|
В b |
А
x
 В1
В1
b1 А |
p |
1 |
1 |
Рис.21
|
|
|
28 |
|
|
а) |
|
z |
|
б) |
z |
|
|
p |
|||
c2 |
K |
c =K |
|
||
3 |
3 |
2 |
|
||
|
2 |
|
|
с2 |
|
|
|
|
|
p |
|
|
|
|
|
с |
|
|
|
|
|
3 |
|
х |
|
|
y |
х |
с3 |
|
|
О |
|
с1 |
|
|
|
|
|
||
c1 |
K1 |
|
|
p1 |
|
y |
|
y |
|||
|
|
|
|
||
|
|
|
Рис.22 |
|
|
Проецирующие прямые на плоскостях проекций, перпендикулярно которым они расположены, изображаются в виде точки.
Проекция прямой в виде точки обладает собирательным свойством: в эту
точку проецируются все точки прямой (на рис. 20 a1 º A1 º N1; на рис. 21 b2 º B2;
на рис. 22 с3 º K3).
Проецирующие прямые на плоскости проекций, параллельно которым
они расположены, проецируются в натуральную величину, например на рис. 20
проекция A2N2 отрезка AN равна натуральной величине отрезка AN.
ЗАДАЧА 1. Построить проекции отрезкаАВ прямой линии,
перпендикулярной плоскости П1 и проходящей через точку А.
Натуральная длина отрезка составляет25 мм. (Проекции точки А задать самостоятельно.) Сколько решений имеет задача?
ЗАДАЧА 2. Построить проекции отрезкаСD прямой линии,
перпендикулярной плоскости П2 и проходящей через точку С.
Натуральная длина отрезка составляет15 мм. (Проекции точки С задать самостоятельно.) Сколько решений имеет задача?
