
- •ВВЕДЕНИЕ
- •ОБОЗНАЧЕНИЯ И СИМВОЛИКА
- •Д3. Аксонометрия
- •Д4. Метод Монжа. Точка. Проекции точки
- •Д5. Координаты точки
- •Д6. Прямая общего положения. Принадлежность точки прямой
- •Д7. Прямые уровня. Принадлежность точки прямой
- •Д8. Проецирующие прямые
- •Д9. Прямые различного взаимного расположения
- •Д12. Плоскость общего положения. Принадлежность точки плоскости
- •Д13. Проецирующие плоскости. Принадлежность точки плоскости
- •Д15. Условия принадлежности прямой плоскости
- •Д16. Главные линии плоскости
- •Д17. Поверхность. Образование, задание и изображение на чертеже. Принадлежность точки и линии поверхности
- •Д20. Частные виды поверхностей вращения
- •Раздел II. ПОЗИЦИОННЫЕ ЗАДАЧИ
- •Д23. Сечения кривых поверхностей
- •Д24. Цилиндрические сечения
- •Д25. Конические сечения
- •Д26. Сферические сечения
- •Д27. Сечения многогранников
- •Д28. Пересечение поверхностей
- •Д30. Способ вспомогательных секущих плоскостей
- •Д31. Пересечение соосных поверхностей вращения
- •Д32. Способ концентрических сфер
- •Д33. Теорема Монжа
- •Раздел III. МЕТРИЧЕСКИЕ ЗАДАЧИ.
- •Д36. Способ замены плоскостей проекций
- •КОНТРОЛЬНЫЕ ВОПРОСЫ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
83
аналогично радиусам r1 и r2. Построение проекций промежуточных точек показано на примере точек 1 и 2.
4. Соединяются точки с учетом ихвидимости на плоскостяхП1 и П2.
Фронтальные проекции видимых и невидимых наП2 |
точек линии пересечения |
|||||||
поверхностей |
совпадают, |
так |
как |
линия |
пересечения |
симметрична |
||
относительно |
плоскости α||П2. На |
чертеже |
фронтальная |
проекция |
линии |
|||
изображается |
видимой. На |
горизонтальной |
плоскости |
проекций |
,точки |
|||
расположенные выше плоскостиβ (граница видимости |
наП1), являются |
|||||||
видимыми. Этот участок линии(М1А1Ν1) изображается видимым и далее |
||||||||
переходит в видимую окружность горизонтального очерка сферы. |
|
|||||||
Для придания чертежу большей наглядности |
следует |
определить |
||||||
видимость очерков поверхностей на плоскостях проекций. |
|
|
||||||
Д31. Пересечение соосных поверхностей вращения
Соосными называются поверхности вращения, имеющие общую ось.
Свойство соосных поверхностей вращения: две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей.
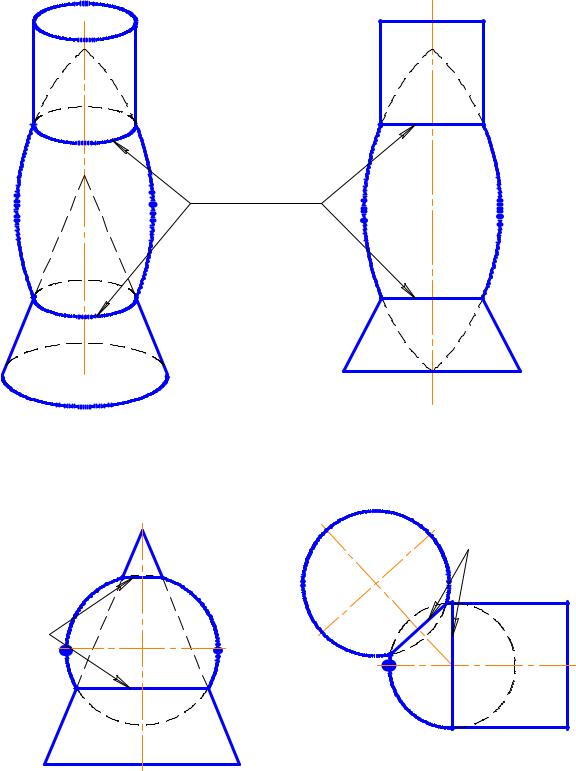
На рисунках 105 и 106 видно, что общие точки А и В меридианов соосных поверхностей цилиндра и тора, тора и конуса при вращении вокруг осиi
описывают окружности, общие для данных поверхностей. Эти окружности представляют собой линии пересечения этих поверхностей.
Втом случае, если одна из поверхностей вращения– сфера,
рассмотренное свойство формулируется так:
если центр сферы находится на оси какой-нибудь поверхности вращения, то сфера соосна этой поверхности и пересекает ее по окружностям, число которых
равно числу точек пересечения(касания) главных меридианов этих
84
поверхностей (рис.107 и 108). Это свойство положено в основу способа концентрических сфер (Д32).
i2
i
A |
A2 |
|
окружность |
B |
B2 |
Рис.105 |
Рис.106 |
|
i2 |
|
A2 |
окружность |
O |
|
2 |
B2 |
|
i2 |
|
окружность |
|
O |
i2 |
2 |
|
C |
|
2 |
|
D2 |
|
Рис.107 |
Рис.108 |
85
Соосные поверхности – сфера и конус, главные меридианы которых пересекаются в двух точкахА и В, изображены на .рис107. Линиями пересечения этих поверхностей будут две окружности, проходящие через точки
А и В.
Две соосные сферы, пересекающиеся по окружности, проходящей через точку С, и соосные сфера и цилиндр, линией касания которых будет окружность, проходящая через точку D, изображены на рис.108.
|
Д32. Способ концентрических сфер |
|
|
|
||||
Способ |
концентрических |
сфер |
применяется |
при |
построении |
лини |
||
пересечения таких поверхностей, которые имеют общую плоскость симметрии, |
|
|||||||
расположенную параллельно какой-либо плоскости проекций. При этом каждая |
|
|||||||
из поверхностей должна содержать семейство окружностей, по которым ее |
|
|||||||
могут пересекать вспомогательные сферы, общие для обеих поверхностей. В |
|
|||||||
частности, способ вспомогательных сфер можно принять |
при построении |
|||||||
линии пересечения поверхностей вращения, оси которых пересекаются и |
|
|||||||
параллельны какой-либо плоскости проекций. |
|
|
|
|
||||
Сферы-посредники |
могут |
проводится |
из |
одного |
-центраспособ |
|
||
концентрических сфер или из разных центров способ эксцентрических сфер.
Применение способа концентрических сфер возможно, если:
-обе пересекающиеся поверхности являются поверхностями вращения;
-оси поверхностей пересекаются;
- плоскость общей |
симметрии поверхностей |
параллельна какой-либо |
плоскости проекций. |
|
|
В основу способа положено свойство пересечения соосных поверхностей |
||
вращения, рассмотренное |
в 31:Д сфера пересекает |
любую соосную ей |
поверхность по окружности. |
|
|
86
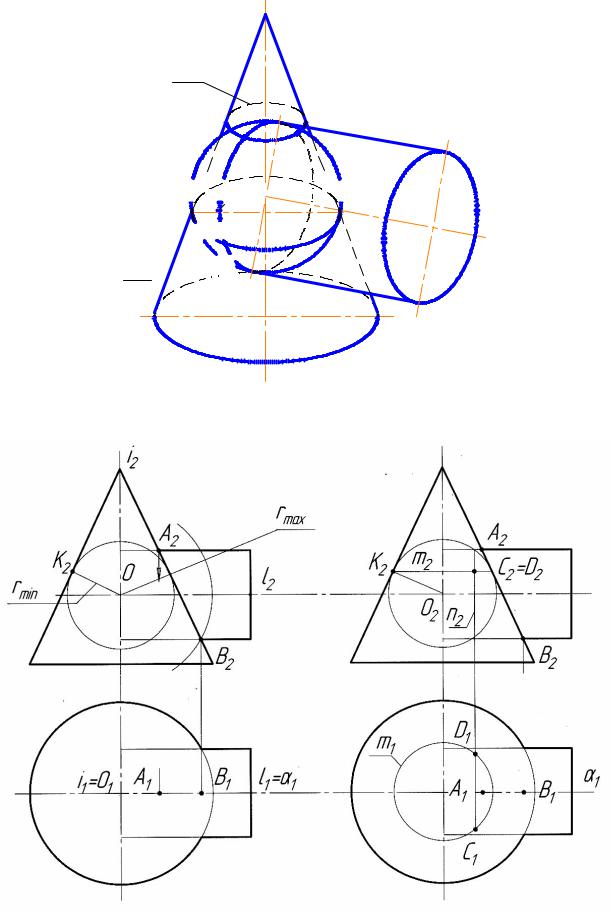
Нахождение четырех общих точек пересекающихся поверхностей конуса
и цилиндра с помощью вспомогательной сферы, соосной обеим поверхностям,
показано на рис.109
Вспомогательная сфера пересекает поверхность конуса по окружностям
m1 и m2, а поверхность |
цилиндра– по окружности n. |
Точки 1 и 2, 3 и 4 |
получены в пересечении построенных окружностей m1 и m2 с окружностью n. |
||
Сущность способа |
концентрических сфер |
рассмотрена на примере |
решения задачи на построение линии пересечения поверхностей конуса и цилиндра (рис. 110 - 113).
Анализируя |
условие |
задачи, можно |
установить, |
что |
заданные |
|
поверхности являются поверхностями вращения. Оси l и i этих поверхностей |
||||||
пересекаются |
в |
точкеО и |
расположены в плоскостиα и |
параллельнойП2 |
||
(рис.110). |
|
|
|
|
|
|
Таким образом, в данной задаче целесообразно использовать способ |
||||||
концентрических сфер, принимая за центр точку О. |
|
|
||||
Последовательность построения следующая. |
|
|
|
|||
1. Определяется положение плоскости симметрии. Ею является плоскость |
||||||
α, в которой |
расположены |
осиl и i заданных |
поверхностей. Эта |
плоскость |
||
параллельна плоскости П2, поэтому сначала строятся фронтальные проекции точек лини пересечения.
2.Находятся опорные точки. А и В - высшая и низшая точки кривой. Они принадлежат плоскости симметрииα и находятся с помощью этой секущей плоскости по общему алгоритму (Д.30 рис.104). Все остальные точки, опорные и промежуточные, находятся с помощью концентрических сфер с центрами в точке О.
87
m2
3 |
(4) |

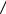


 n О
n О (2)
(2)













 1 m1
1 m1 







Рис.109
Рис.110 |
Рис.111 |
88
Рис.112 Рис.113
Сначала следует определить радиусы максимальной и минимальной сферы,
позволяющие отыскать некоторые опорные точки.
Минимальная сфера должна касаться одной заданной поверхности и пересекать другую поверхность. Чтобы определить радиус минимальной сферы
rтin, необходимо провести через точкуО нормали к очерковым образующим данных поверхностей. Больший из отрезков этих нормалей и будетr in.. В
данном примере rтin=О2К2 (рис.110).
Радиус максимальной сферы равен расстоянию от точкиО до наиболее удаленной опорной точки. В данном примере rтax=О2В2.
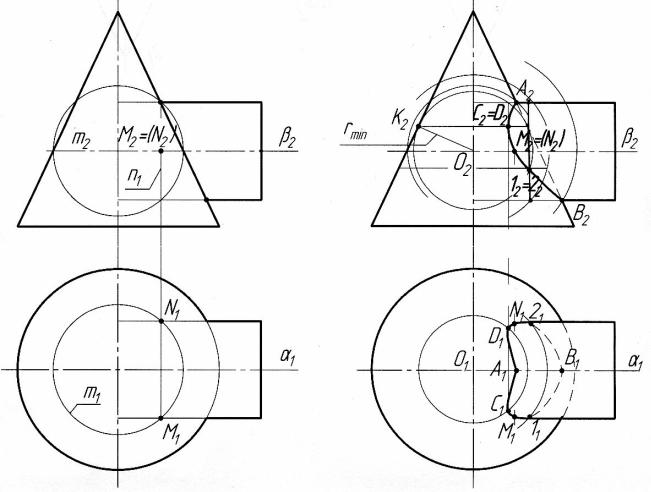
Опорные точки С и Д определяются с помощью минимальной сферы
(рис.111) по следующему алгоритму:
89
1) проводится вспомогательная сфера минимального радиуса. На чертеже
построена фронтальная проекция сферы в виде окружности; |
|
|||||||||
2) |
строится |
окружность m, |
по |
которой |
сфера |
касается |
поверхности |
|||
конуса. |
Строится |
|
окружность n, по |
которой сфера |
пересекает |
поверхность |
||||
цилиндра. Фронтальные проекции окружностейm и n изображаются в виде |
||||||||||
отрезков m2 и n2; |
|
|
|
|
|
|
|
|
||
3) точки С и D находятся на пересечении окружностей m и n. |
|
|||||||||
На чертеже определяются фронтальные проекцииС2=D2 в пересечении |
||||||||||
отрезков m2 и n2. |
Горизонтальные |
проекции С1 |
и D1 |
строятся |
с помощью |
|||||
окружности |
m, |
которая |
проецируется на |
горизонтальную |
плоскость без |
|||||
искажения в виде окружности m1. |
|
|
|
|
|
|||||
М и |
Ν - |
точки |
видимости |
наП1. Они |
принадлежат плоскостиβ, |
|||||
определяющей границу видимости цилиндра наП1 (вся поверхность конуса видима на П1). Для нахождения точек М и Ν надо выбрать такую сферу, которая пересекла бы конус по окружности(m'), расположенной в плоскостиβ (рис. 112). Эта сфера пересекает поверхность цилиндра по окружностиn' , а конус -
по двум окружностям, одна из которых m' пересекается с окружностью n', давая точки М и Ν. Горизонтальные проекции М1 и Ν1 точек М и Ν расположены на образующих горизонтального очерка цилиндра.
3. Строятся промежуточные точки с помощью сфер, адиусы которых
выбираются |
в пределахrтin<r<rтax. |
Построение |
промежуточных |
точек |
аналогично построениям точек С и D, М и Ν (рис.113) |
|
|
||
4. Точки |
соединяются с учетом |
их видимости на плоскостяхП1 |
и П2 |
|
(рис.113). Фронтальные проекции видимых и невидимых наП2 точек линии пересечения совпадают, так как линия симметрична относительно плоскости
α||П2 . На чертеже фронтальная проекция изображена видимой.
На горизонтальной плоскости проекций точки, расположенные выше плоскости β (граница видимости наП1), являются видимыми. Этот участок линии (Ν1D1А1С1М1) изображается видимым, дальше он переходит в видимый
