Это уравнение следует дополнить граничным условием, состоящим в том, что ионы не могут попадать на анод

Таким образом, ток ионов в промежутке мы выразили через ток электронов в промежутке, который, в свою

очередь, однозначно определяется током эмиссии электронов с катода ie 0, t − z , а он – граничным

we

условием (2.1.18), учитывающим как внешний источник, так и вторичные процессы на катоде. Цепь замкнулась. Набор упомянутых уравнений позволяет вычислить все токи в промежутке. Теперь можно перейти к определению тока во внешней цепи.

2.1.4.Ток во внешней цепи

Перемещение любого заряда в промежутке индуцирует смещение зарядов во всей электрической цепи. Ток во внешней цепи равен полному току в промежутке, определяемому для каждого из носителей (электроны, положительные и отрицательные ионы) в соответствии с теоремой о среднем:

Вероятность образования отрицательных ионов (которые нередко появляются за счет прилипания электронов к нейтральным частицам на стадии распада плазмы) в процессе пробоя газа обычно невелика, поэтому далее исключим их из рассмотрения.

Примем, для простоты, что в начальный момент из катода мгновенно испускается N0 электронов, ини-

Здесь индекс (1) означает, что выражение описывает “первичные” токи, которые связаны только с процессом размножения частиц при пролете лавины через газовый промежуток.

122

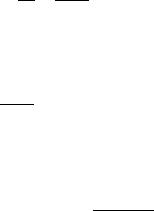
Теперь перейдем к вычислению ионного тока. Прежде чем воспользоваться теоремой о среднем (2.1.25), возьмем интеграл в выражении тока ионов в промежутке ip(z, t)

Смысл ограничения на время ясен из рис. 57. До прихода электронов в плоскость z (момент t = z/we) ионный ток в этой плоскости также отсутствует. Далее в каждый момент времени t в плоскость z приходят

ионы из некоторой выше лежащей плоскости y, удовлетворяющей условию

t = y + y − z we wp

Ток прекращается после прихода ионов, рожденных непосредственно у анода. Это произойдет в момент времени

Теперь можно взять вышеупомянутый интеграл по промежутку, что и даст нам ток во внешней цепи,

Мы обозначили здесь верхний предел интегрирования буквой ζ, чтобы отметить, что до того как электроны достигнут анода (при t < Te), ионы реально существуют только в “нижней” части промежутка в области, где прошла электронная лавина z ≤ wet. После того как электроны уидут на анод (t > Te), верхняя граница этой области движется от анода к катоду вместе с дрейфующими ионами: zmax = d − wp(t − Te).

Подставив подчеркнутые величины z в качестве верхней границы интегрирования ζ и объединив вместе

обе экспоненты, получим выражение для “первичного” ионного тока в цепи:

Полученные выражения достаточно понятны. Первый член верхнего выражения для ионного тока соответствует электронному току,– число образующихся ионов равно числу образующихся электронов, а амплитуда тока меньше в Te/Tp раз, где Tp = d/wp – время, за которое ион, рожденный возле катода,

123

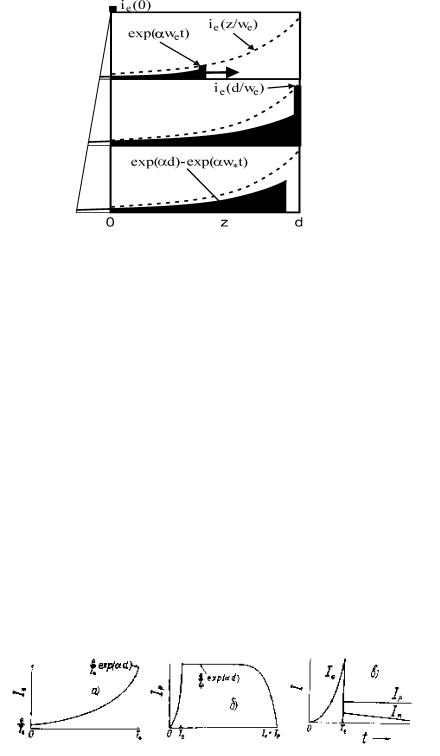
Рис. 59: Схема распределения ионов в промежутке при прохождении электронной лавины, вызванной “мгновенной” эмиссией электронов с катода, для трех последователььных моментов времени:

(а) электронная лавина (обозначена толстым столбиком) вблизи середины промежутка, (б) электронная лавина достигла анода, (в) дрейф ионного “шлейфа” после ухода электронов из промежутка. Площадь под кривой правее z = 0 пропорциональна току во внешней цепи Ip, вызванному движением ионов в промежутке. Вторичная эмиссия с катода не учитывается.

пересекает межэлектродный промежуток. Второй член верхнего выражения учитывает уход части ионов на катод. Графически это изображено на рис. 59. Ток в цепи как функция времени показан на рис. 60, где отношение (Ip(1)/Te(1))max сильно преуменьшено. Таким образом, для случая одиночной лавины, не сопровождаемой вторичной эмиссией с катода, во внешней цепи наблюдается короткий импульс “электронного” тока, завершающийся длинным импульсом “ионного” тока.

В электроотрицательных газах возможно прилипание электронов, конкурирующее с ионизацией атомов электронным ударом. Введя, аналогично первому коэффициенту Таунсенда α, коэффициент прилипания a,

Рис. 60: (а) К вычислению первичных токов во внешней цепи; (б) Токи во внешней цепи, вызываемые движением электронов и ионов в промежутке; (в) Токи с учетом отрицательных ионов.

124

запишем для этого случая коэффициенты размножения

Единица в последних двух выражениях появляется из-за того, что электроны, эмиттированные в начальный момент из катода, не имеют соответствующих им ионов, тогда как остальные заряженные частицы рождаются парами. Ток отрицательных ионов In спадает быстрее, чем Ip, так как большая часть отрицательных ионов сосредоточена вблизи анода, на который они и уходят, тогда как положительным ионам, плотность которых также максимальна вблизи анода, нужно продрейфовать через весь промежуток к катоду.

125