Лекция 7

1.8.ФРЭ в молекулярном газе

Функция распределения электронов в молекулярном газе не может быть описана ни максвелловской, ни дрювестейновскими функциями. В свое время, в связи с исследованиями газовых лазеров, где знание (и управление) функцией распределения является ключевой проблемой, определяющей эффективность генерации, были проведены широкие экспериментальные исследования и выполнен целый ряд численных расчетов по вычислению ФРЭ в молекулярных газах.

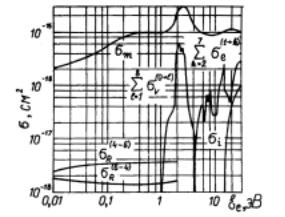
Рис. 47: Сечения элементарных процессов для молекулы азота. Обозначения – стандартные.

Наиболее детальными численными расчетами, в которых использовались точные зависимости сечений интересующих процессов от энергии столковения, были расчеты Найана [45]. Несколько позже Эллис и Хаус [46] опубликовали статью, где подобные расчеты были выполнены на основе простой (если не сказать примитивной) модели функций возбуждения, позволившей решить задачу аналитически. Их “молекула” имела лишь один колебательный и один электронный уровень. Процессами ионизации пренебрегалось вообще (низкотемпературная плазма). Эта работа весьма показательна, так как дает представление и о методике численных расчетов, и позволяет лучше понять вклад разных процессов в вид функции распределения. Самое интересное, что результаты, полученные с помощью их модели не так уж плохо совпадают с численными расчетами Найана. В данном разделе мы получим ФРЭ, основываясь на модели Эллиса и Хауса.

Итак, слабоионизованный молекулярный газ находится в постоянном электрическом поле E. Характерная средняя энергия электронов в таких случаях равна 1 ÷ 3 эВ. Из приведенных на рис.47 сечений элементарных процессоров для молекулы азота видно, что в этом интервале, кроме траспортного сечения, существенными являются сечение возбуждения колебаний молекулы и сечение возбуждения нижних электронных состояний. Поскольку сечение колебателного возбуждения сравнимо с сечением упругого рассеяния

σm, а эффективность передачи энергии в упругом столкновении мала ( m/A · mp 10−4), то в данном случае можно пренебречь упругими столкновениями при расчетах формирования функции распреде-

105

ления. Порог сечения ионизации также достаточно велик, и ее ролью в формировании ФРЭ также можно

Перейдем в этом выражении к функции распределения по энергии, выраженной теперь не в эрг, а в эВ,

введя новую переменную

ε эрг = u [эВ] .

ee

Используя, в соответствии с Приложением A, соотношение (A.0.4) между f(ε) и f0(v), обе части которого домножим на e3/2, и опуская индекс 0 (f0 −→ f), получим для ФРЭ, отнесенной к энергии в электронвольтах, выражение

Здесь введена ФРЭ

f(u) = f0(ε) · e3/2 .

Размерность f(u) есть [эВ−3/2]. Поскольку

= mv2 u 2e ,

то

v2 = 2e u m

и

dv = 1 2e 1/2 u−1/2 du .

2m

теперь легко перейти к f(u). Из уравнения видно, что для этого нужно в левой и правой частях df(v) просто заменить на df(u), а v2 на u. Подставив, оставшиеся “нескомпенсированными” d/dv

106

Ясно, что Sinel – есть “источник” электронов на единицу энергетического диапазона ([−1]), связанный с неупругими столкновениями. Обозначим член в скобках (−GE).По смыслу это “ток” в пространстве энергий. В результате получаем уравнение

являющееся уравнением непрерывности по оси энергии.

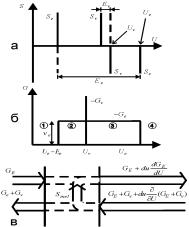
Рис. 48: К выводу уравнения непрерывности, (а) функции источников, (б) потоки, (в) схема по-

токов в пространстве энергий.

Полученное уравнение может быть решено, если конкретизировать функцию источника Sinel. Схематически уравнение иллюстрируется рис. 48,а. GE похоже на ток проводимости в среде, только он E2, а не E.

Предположим, что электроны набирают энергию от поля, а теряют только за счет двух процессов,– возбуждения одного электронного уровня и одного колебательного уровня молекулы. Сильно упрощая ситуацию, принимаем что энергичные электроны, достигая порога возбуждения ue, возбуждают электронный уровень Ee и возвращаются “назад”, “перескакивая” в интервал вблизи u = ue − Ee (здесь все энергии измеряются в эВ). Для такой модели “источник” для электронного возбуждения представляется (см. рис. 48,б) δ-функцией

107

При этом энергия электронов в принципе не может превысить энергию Ee. Точно также для колебательного возбуждения можно записать

Если бы EV было большим, то электроны не преодолели бы энергию uV , но в отличие от электронного возбуждения, где εe и Ee - величины одного порядка и “скачок” по шкале энергии очень большой, величина

Ee << uV . Поэтому можно апроксимировать правую часть производной от δ-функции, положов du EV ,

SV (u) +νV dδ(u − ue) · EV . (1.8.11) du

которое иллюстрируется схемой рис. 48,в и отражает закон сохранения числа электронов (ионизация в нашей модели отсутствует). Эти потоки легко получаются интегрированием δ-функции (Se) и производной

δ-функции (SV ) и имеют вид

108

Чтобы его решить, нужно знать зависимость νm(v). Примем, для простоты, что νm =const. Введем кроме того “дрейфовую энергию”, которую определим выражением:

Далее, проще вычислить интеграл, начиная с правой границы. Учитывая требование равенства ФРЭ нулю при бесконечной энергии, сразу запишем ФРЭ для области 4

Это выражение одновременно является граничным условием для ФРЭ в интервале 3. Отсюда получим

Таблица 7: Типы функции распределения электронов, наблюдавшиеся экспериментально в разных

газах: FM – Максвелла, FD– Дрюйвестейна, FN – Найана

109

Рис. 49: Функция распределения электронов в азоте: (а) вычисленные по упрощенной модели; (б) численно расчитанные Найаном.

Рис. 50: Эффектиность возбуждения колебательных уровней в молекуле CO, вычисленные по упрощенной модели Эллиса и численно расчитанные Найаном.

Выражения (1.8.22), (1.8.25), (1.8.24) и (1.8.23) описывают модельную ФР для электронов в молекулярном газе.

В заключение раздела приведем модельную ФР f(u) для молекулы азота, приняв uV = 2 эВ, EV = 0.2 эВ, ue = Ee = 10 эВ, и сравним ее (см. рис. 49,а) с численными расчетами, Найана (рис. 49,б), выполненными с реальными сечениями с учетом всех уровней. Видно, что даже крайне примитивная модель дает

110