Легко видеть, что верхние (ридберговские) состояния атомов имеют очень большое время жизни по сравнению с нижними ( k−5). Поскольку и энергия связи их сопоставима с температурой газа, то заселенность верхних уровней в значительной мере определяется столкновениями. С ростом плотности вероятность столкновительных переходов начинает превышать вероятность испускания фотона для все более глубоких уровней.

1.4.4.Доплеровское уширение. Фойгтовский профиль

Для изолированного атома контур линии – лоренцовский (1.4.26), и естественная ширина линии γ ≡ γkm

равна сумме радиационных ширин начального γk и конечного γm состояний. Поскольку атомы и ионы плазмы движутся, то происходит смещение спектральной линии излучающего атома вследствие эффекта Доплера

v · n

ω = ω0 1 + c , (1.4.40)

где n – единичный вектор в направлении наблюдения. Если распределение атомов по скоростям максвелловское, то вероятность, что составляющая скорости в направлении наблюдения равна [vx, vx + dvx] есть

Контур линии, описываемый выражением (1.4.43), называют доплеровским. Полуширина (ширина на половине высоты) доплеровской линии δ равна

Поскольку доплеровское и естественное уширение происходят одновременно и независимо, то результирующий контур является сверткой лоренцовского и доплеровского контуров:

64

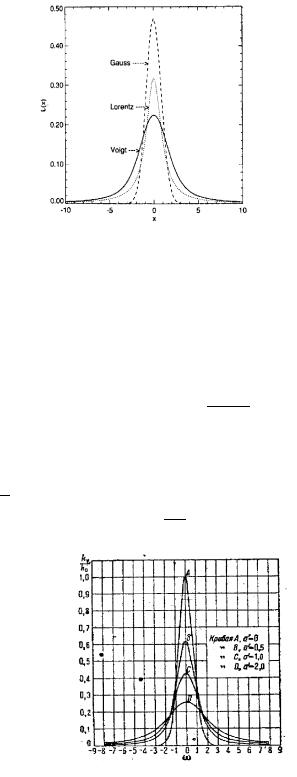
Рис. 25: Контуры линий лоренцевского, доплеровского и фойгтовского профилей [31].

Это выражение справедливо для любого распределения p(v). Если распределение максвелловское, то используя стандартные обозначения [29]

√

Здесь ε0 = 1/ π∆ωD – интенсивность в максимуме линии, а H(a, u) – функция Фойгта. Ее вид в зависимости от величины a = (∆ωL/∆ωD)√ln 2 показан на рис. 26.

Рис. 26: Лоренцевское уширение доплеровской линии [32], стр.145.

Коэффициент поглощения линии с фойгтовский контуром равен

65

–интеграл ошибок.

Впредельном случае a << 1, когда доплеровское уширение много больше естественного, в центральной части линии контур становится чисто доплеровским. На далеких крыльях линии (см. рис. 25), однако, контур всегда остается дисперсионным.

1.4.5.Уширение давлением

Уширение спектральных линий, связанное с взаимодействием излучающей атомной системы с окружающей средой, носит общее название “уширение давлением”. При сближении с другими частицами происходит изменение силового поля в окрестности возбужденного атома, а следовательно, происходит изменение энергии электронных термов. С современным уровнем квантово-механической теории уширения давлением и основными экспериментальными результатами в этой области можно познакомиться в монографии [30]. Из доступных книг можно порекомендовать [23, 24, 29, 31, 32, 33, 34, 35]. В данном параграфе мы очень сжато изложим основные понятия теории уширения давлением в объеме, минимально необходимом для понимания процессов в низкотемпературной плазме, исходя из простейшей теории возмущения классического осциллятора окружающими частицами (см. [23, 24, 29, 35]).

В большинстве случаев в низкотемпературной плазме основную роль играют парные столкновения. Гамильтониан атома изменяется при столкновении на величину

V (R) = − RCnn , (1.4.52)

где Cn - константа, а n - целое число, зависящее от вида взаимодействия. В квазиклассическом приближении (считаем возмущение адиабатическим, то есть не приводящим к переходам между состояниями, а траекторию прямолинейной) на атом накладывается внешнее поле

где t = 0 – момент наибольшего сближения, а v – относительная скорость. Сдвиг частоты перехода при этом равен

66

где n = 2 для линейного и n = 4 для квадратичного штарк-эффекта.

Предположим сначала, что продолжительность соударения мала по сравнению с временем между соударениями (“ударное приближение” Лорентца, Ленца, Ландхольма). Тогда контур линии, излучаемой со-

где сечения, определяющие уширение и сдвиг линии,

∞

σ= 2π [1 − cos η(ρ)] ρ dρ ,

0

∞

σ= 2π sin η(ρ) ρ dρ

0

зависят от полного сдвига фазы колебаний осциллятора за время столкновения

Контур при ударном уширении (1.4.55), подобно естественному контуру, имеет дисперсионный вид. Выражения для вычисления уширения γ ≡ Nvσ и сдвига ∆ ≡ Nvσ для линейного эффекта Штарка (n=2), резонансного уширения при взаимодействии атомов одного и того же элемента (n=3), квадратичного эффекта Штарка (n=4) и уширения Ван-дер-Ваальса (n=6) приведены, например, в [29, 34]. Для оценок естественно считать “сильными” столкновения, для которых η 1. Это соответствует пролетам с

Характерное время столкновения равно τc ρB/v, а соответствующая частота ΩB = 1/τc называется вайскопфовской. В согласии с принципом Месси контур (1.4.55) правильно описывает форму линии при условии ∆ω τc 1. Центральную часть линии, удовлетворяющую условию ∆ω ΩB, называют ударной. Ее ширина может превосходить естественную ширину на много порядков. В обратном случае

∆ω τc 1 атом находится в поле действия других частиц, которое меняется достаточно медленно по сравнению со временем спонтанного излучения. В этом случае справедливо “статическое” (“квазистатическое”, “статистическое”) приближение . Для вычисления контура линии достаточно найти плотность распределения осцилляторов по частотам. Будем считать, что основное поле создает ближайшая частица (приближение

“ближайшего соседа”). Вероятность нахождения ближайшей частицы на расстоянии R, R + dR равна

67