
get_2 физика
.pdfВ.Ф. Аскирка, В.В. Война, А.М. Колодинский, А.А. Маскевич
МЕХАНИКА, МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Учебное пособие для студентов инженерно-технических специальностей учреждений,
обеспечивающих получение высшего образования
Допущено Министерством образования Республики Беларусь
Учреждение образования «Гродненский государственный университет
имени Янки Купалы» 2005
УДК 531+539.19+536 ББК 22.2
А90
Рецензенты: кафедра физики БГТУ (зав. кафедрой – доктор физико-математических наук, профессор И.И. Наркевич);
заведующий кафедрой технической физики БНТУ, кандидат физико-математических наук, доцент Е.Е. Трофименко.
Аскирка, В.Ф.
Механика, молекулярная физика и термодинамика : учеб. А90 пособие / В.Ф. Аскирка [и др.]. – Гродно : ГрГУ, 2005. – 184 с.
ISBN 985-417-713-0
Учебное пособие содержит теоретические сведения, основные законы и формулы, примеры решения задач, а также задания к индивидуальным и контрольным работам по разделам «Механика», «Молекулярная физика и термодинамика» из курса «Физика». Включены справочные материалы, необходимые для решения задач.
Предназначено для студентов инженерно-технических специальностей дневных, вечерних и заочных отделений.
УДК 531+539.19+536 ББК 22.2
ISBN 985-417-713-0
© Аскирка В.Ф., Война В.В., Колодинский А.М., Маскевич А.А., 2005
2
ВВЕДЕНИЕ
Важной задачей курса «Физика» для студентов инженернотехнических специальностей является формирование навыков физического моделирования прикладных задач будущей специальности. Решение этой задачи невозможно без прочного знания основных физических явлений и законов, а также усвоения приемов и методов практического использования полученных знаний. В этой связи большое значение имеет самостоятельная работа студентов над индивидуальными практическими заданиями.
Целью настоящего учебного пособия является оказание помощи студентам инженерно-технических специальностей при изучении курса «Физика» и, прежде всего, при решении задач контрольных и индивидуальных заданий.
Данная книга представляет собой первую часть пособия, адресованного студентам как дневных, так вечерних и заочных отделений. Она включает в себя разделы «Механика» и «Молекулярная физика и термодинамика». В начале каждого из них даны основные понятия и определения, а также законы и формулы, снабженные необходимыми пояснениями. Приведено значительное количество примеров решения типовых задач. В этой части пособия содержится более 500 задач к индивидуальным и контрольным работам. Для составления различных вариантов заданий преподаватель имеет возможность широко комбинировать задачи из разных разделов на свое усмотрение. Для экономии времени студентов в приложении представлен справочный материал, необходимый для решения задач, предлагаемых в пособии. Для удобства студентов-заочников приложение снабжено правилами по выполнению и требованиями к оформлению контрольных работ.
Необходимость подобного рода издания продиктована отсутствием таковых в достаточном количестве, а также наблюдающимся увеличением числа студентов инженерно-технических специальностей. Содержание пособия к тому же ориентировано на максимально самостоятельную работу студента.
Авторы выражают искреннюю признательность заведующему кафедрой физики БГТУ, профессору Наркевичу И.И., доценту ка-
3
федры Илюшонок И.П., ассистенту Долгий В.К., а также заведующему кафедрой технической физики БНТУ, доценту Трофименко Е.Е. за тщательное рецензирование книги и сделанные замечания, в значительной мере способствовавшие ее улучшению.
Авторы выражают также глубокую благодарность старшему преподавателю кафедры общей физики ГрГУ Кукреш М.И. за ценные советы и замечания, сделанные в процессе работы над рукописью.
Авторы будут также признательны всем за высказанные замечания и предложения, касающиеся содержания настоящего пособия.
4
МЕХАНИКА
1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. КИНЕМАТИКА
Механика – раздел физики, в котором изучаются закономерности механического движения, а также причины, вызывающие или изменяющие это движение.
Механическое движение – изменение взаимного расположения тел или частей одного тела с течением времени.
Кинематика изучает движение тел без рассмотрения причин, вызывающих это движение.
Основной задачей кинематики является определение закона движения тела, или, другими словами, определение местоположения его в пространстве в определенный момент времени. Обратная задача кинематики – определение кинематических характеристик (скорости, ускорения) по известному закону движения.
Тело, обладающее массой, размерами которого в данных условиях можно пренебречь, называется материальной точкой. Произвольно выбранное абсолютно твердое тело, относительно которого определяется положение других тел, называют телом
(началом) отсчета.
Системой отсчета называется система координат (преимущественно прямоугольной декартовой), снабженная часами и связанная с телом отсчета, по отношению к которому определяется положение других тел в различные моменты времени (рис. 1.1).
Радиус-вектор r |
– это вектор, соединяющий начало отсчета с |
||
точкой, в |
которой |
находится тело |
в данный момент времени |
(рис. 1.1): |
|
|
|
r |
+ y(t) j + z(t)k , |
(1.1) |
|
r (t) = x(t)i |
|||
где (i , j, k ) – единичные векторы (орты) осей прямоугольной системы координат; x(t), y(t), z(t) – координаты точки в момент времени t .
Перемещение (приращение радиус-вектора) r – вектор,
соединяющий начальную и конечную точки траектории, по кото-
5
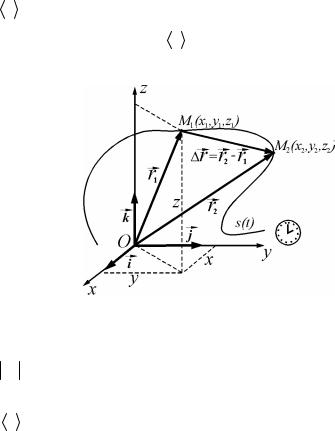
рой двигалась материальная точка в промежутке времени t
(рис. 1.1).
Траектория – линия, вдоль которой движется тело. Длина траектории называется пройденным путем.
Средняя скорость неравномерного движения – векторная физическая величина, определяемая отношением вектора перемеще-
ния |
r к промежутку времени |
t , за который произошло это пе- |
|
ремещение: |
|
||
r |
r |
|
|
r . |
(1.2) |
||
υ = |
|||
|
t |
|
|
|
r |
|
|
Вектор средней скорости υ совпадает по направлению с векто- |
|||
ром перемещения r . |
|
||
Рис. 1.1
Модуль средней скорости – отношение модуля перемещения
r
r к промежутку времени, за который произошло это пере-
мещение: |
|
||||||
|
|
|
|
r |
|
|
|
|
r |
|
|
r |
|
|
|
|
υ |
= |
|
t |
|
. |
(1.3) |
|
|
|
|
6 |
|||
|
|
|
|
|
|
|
|
Средняя путевая скорость – отношение всего пути s к про-
межутку времени t , за который этот путь прошла материальная точка:
υ = |
s |
. |
(1.4) |
|
|||
|
t |
|
|
Равномерным движением называется такое движение, при котором материальная точка (тело) за любые равные промежутки времени совершает равные перемещения.
Вектор мгновенной скорости u (скорости в данной точке траектории) равен пределу отношения вектора перемещения r к
интервалу времени t |
при t , стремящемся к нулю, т.е. первой |
||||
производной перемещения по времени: |
|||||
|
r |
|
r |
(1.5) |
|
u = lim Dr |
= dr . |
||||
r |
|
|
|
|
|
|
t→0 Dt |
|
dt |
|
как и вектор dr , направлена по касатель- |
Мгновенная скорость, |
|||||
ной к траектории движения (в рассматриваемой точке).
Модуль мгновенной скорости может быть найден с помощью следующих соотношений:
|
r |
|
|
|
|
|
|
æ dx ö2 |
æ dy ö2 |
æ dz ö |
2 |
ds |
|
|
||||||
|
|
|
2 |
2 |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
u = |
u |
|
= |
ux |
+ uy + uz |
= |
ç |
|
÷ |
+ ç |
|
÷ |
+ ç |
|
÷ |
= |
|
, |
(1.6) |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
è dt ø |
è dt ø |
è dt ø |
|
dt |
|
|
||||||
где ds – путь, пройденный точкой за время dt , ux = dxdt , uy = dydt
и uz = dzdt – проекции вектора скорости на оси x, y и z соответст-
венно.
r
Средним ускорением a неравномерного движения называет-
ся векторная величина, равная отношению изменения скорости Du к интервалу времени t , за который это изменение произошло:
7

r |
|
Du |
|
a |
= |
Dt . |
(1.7) |
Модуль среднего ускорения – отношение изменения модуля
скорости |
υ к промежутку времени, в течение которого это изме- |
||
нение произошло: |
|||
a = |
Du |
. |
(1.8) |
|
|||
|
Dt |
|
|
Вектор мгновенного ускорения а равен пределу отношения вектора изменения скорости Du к интервалу времени t при t , стремящемся к нулю, то есть первой производной вектора скорости по времени, или, что то же самое, – второй производной ради-
ус-вектора r |
по времени: |
|
|||||||
r |
|
r |
|
r |
|
r |
|
|
|
|
Du |
|
du |
|
d 2 r |
|
|
||
a |
= lim |
|
= |
|
= |
|
. |
(1.9) |
|
Dt |
dt |
dt 2 |
|||||||
|
t→0 |
|
|
|
|
||||
Направление вектора ускорения совпадает с направлением вектора изменения скорости.
Модуль мгновенного ускорения может быть определен из соотношений:
|
r |
|
|
|
|
|
|
|
|
æ d 2 x ö2 |
æ d 2 y ö2 |
æ d 2 z ö |
2 |
d 2 s |
|
||||||||||
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
a = |
a |
= |
a |
|
+ a |
|
+ a |
|
= |
ç |
|
|
÷ |
+ ç |
|
|
÷ |
+ ç |
|
|
÷ |
= |
|
|
, (1.10) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x |
|
y |
|
z |
|
ç |
dt |
2 ÷ |
ç |
dt |
2 ÷ |
ç |
dt |
2 ÷ |
|
dt |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
è |
ø |
è |
ø |
è |
ø |
|
|
|
|||||||
где |
ax = |
d 2 x |
, ay |
= |
d 2 y |
, az |
= |
d 2 z |
– проекции ускорения на оси x, |
||
dt |
2 |
dt 2 |
dt 2 |
||||||||
|
|
|
|
|
|
|
|||||
y и z соответственно. |
|
|
|
|
|||||||
При криволинейном движении вектор ускорения a (в этом случае называемый полным ускорением) можно представить в виде суммы векторов тангенциального aτ (или касательного) и нор-
мального an (или центростремительного) ускорений:
r |
r r |
u2 r |
|
du r |
|
|||
a |
= an + aτ = |
|
n |
+ |
|
t , |
(1.11) |
|
r |
dt |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
8 |
|
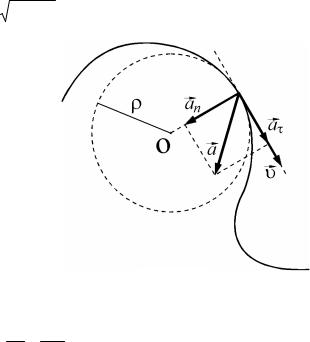
где n и τ – единичные векторы в направлении нормали и касательной к траектории соответственно, ρ – радиус кривизны траек-
тории в данной точке (рис. 1.2).
Нормальное ускорение характеризует изменение направления вектора скорости, а тангенциальное – изменение его модуля. При прямолинейном движении может изменяться только модуль скорости. В этом случае а = аτ .
Модуль полного ускорения определяется выражением:
a = aτ2 + an2 . |
(1.12) |
Рис. 1.2
Модуль тангенциального ускорения:
aτ = dυ = d 22s , dt dt
где υ – модуль мгновенной скорости, s – путь.
Модуль нормального ускорения:
an = υ2 .
ρ
(1.13)
(1.14)
9

Прямолинейное движение, совершаемое с постоянным ускорени-
ем, называется равнопеременным.
Уравнения равнопеременного движения, совершаемого вдоль оси OX :
x = x0 |
+ υ0 x t + ax t 2 2 , |
(1.15) |
||||
υx |
= υ0x + axt , |
(1.16) |
||||
s = υ0x t + ax t 2 2 , |
(1.17) |
|||||
s = |
|
υ2 |
− υ2 |
|
|
|
|
x |
0 x |
|
, |
(1.18) |
|
|
|
2ax |
|
|||
|
|
|
|
|
|
|
где |
|
υ0 x и |
υx – проекции на ось начальной скорости и скорости |
|||
движения в момент времени t , s – пройденный за время t |
путь. |
|||||
Движение тела, которое свободно падает по вертикали (при условии, что ось OY направлена вертикально вниз), описывается уравнениями:
y(t) = y0 |
+ υ0 yt + |
gt 2 |
, |
(1.19) |
|
||||
|
2 |
|
|
|
υy (t) = υ0 y + gt , |
|
(1.20) |
||
где υ0 y и υ y – проекции на ось начальной скорости и скорости движения в момент времени t .
Движение тела, брошенного под углом к горизонту со скоростью υ0 , без учета сопротивления воздуха (при условии, что ось OY
направлена вертикально вверх, а ось OX – горизонтально и тело движется в плоскости XOY ) описывается уравнениями:
y(t) = y0 + υ0 y t − |
gt 2 |
, |
(1.21) |
|
|||
2 |
|
|
|
υy (t) = υ0 y − gt, |
|
(1.22) |
|
x(t) = x0 + υ0 xt, |
|
(1.23) |
|
υx (t) = υ0x = const . |
|
(1.24) |
|
|
|
|
10 |
