get_2 физика
.pdf
Подставив числовые значения и выполнив расчеты, получим,
что значение sin β = 0,845 , тогда b = arcsin(0,845) = 57°40′ .
Построим в точке B «треугольник ускорений» (рис. 1.5). Вектор тангенциального ускорения aτ направлен вдоль вектора
мгновенной скорости uB в данной точке (т.к. модуль скорости увеличивается), то есть по касательной к траектории; вектор нормального ускорения an перпендикулярен вектору мгновенной скорости uB . Из рис. 1.12 видно, что:
aτ = g sin b = guyB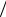 
uB ,
an = g cosb = g 
1 - sin 2 b .
Подставляя числовые значения, находим: aτ = 9,81× 0,85 = 8,3 м/с2,
an = 9,81× 
1 - 0,8452 = 5,25 м/с2.
Радиус кривизны траектории в точке приземления определяем из выражения an = u2B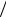 
r . Имеем r = u2B 
an , тогда после подстановки числовых значений:
r = 19,52 = 72,5 м. 5,25
Ответ: uВ =19,5 м/с, b = 57°40′ , aτ = 8,3 м/с2, an = 5,25 м/с2, ρ = 72,5 м.
Пример 7. К нити, перекинутой через неподвижный невесомый блок, подвешены грузы массой 80,0 г и 120 г. С каким ускорением будут двигаться грузы? Какова сила давления на ось блока?
Дано:
m1 = 80 г = 0,80 кг, m2 =120 г = 0,12 кг.
Найти: a, N.
41
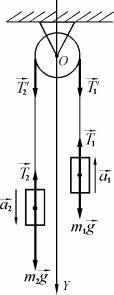
Решение. Грузы массами m1 и m2 будем считать материаль-
ными точками. Ось OY направим вниз, т.е. в направлении ускорения груза с большей массой (рис. 1.13). Ускорения обоих тел одинаковы по величине (нить нерастяжима) и противоположны по направлению.
|
|
|
На тело |
m1 действуют сила тяжести |
|
m1 g и сила натяжения |
|||||||||
нити T1 , на тело m2 |
действуют сила тяжести m2 g и сила натяже- |
||||||||||||||
ния нити T2 . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Второй закон Ньютона [2.1] для обоих тел в векторном виде |
||||||||||||
будет иметь вид: |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
r |
r |
, |
|
|
|
|
|
|
|
(1) |
|
|
|
T1 + m1 g |
= m1a1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
(2) |
|
|
|
T2 + m2 g |
= m2 a2 . |
|
|
|
|
|
||||||
|
|
|
Учитывая знаки проекций векторов на выбранную ось, запи- |
||||||||||||
шем |
|
выражения (1) и (2) в скалярном виде, учитывая, что |
|||||||||||||
|
r |
= |
r |
= a : |
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
a2 |
|
− T1 + m1 g = −m1a , |
|
||||||||||
|
|
|
|
|
|
|
(3) |
||||||||
|
|
|
|
|
|
|
− T2 + m2 g = m2 a . |
(4) |
|||||||
|
|
|
|
|
|
|
Так как нить и блок невесомы, тре- |
||||||||
|
|
|
|
|
|
|
ния на оси блока нет, то T1 |
= T2 = T . По- |
|||||||
|
|
|
|
|
|
|
этому (3) и (4) перепишем в виде: |
||||||||
|
|
|
|
|
|
|
m1 g − T = −m1a , |
(5) |
|||||||
|
|
|
|
|
|
|
m2 g − T = m2 a . |
(6) |
|||||||
|
|
|
|
|
|
|
Решив систему уравнений (5) и (6), |
||||||||
|
|
|
|
|
|
|
получим выражения для нахождения ус- |
||||||||
|
|
|
|
|
|
|
корения и силы натяжения нити: |
||||||||
|
|
|
|
|
|
|
a = g |
m2 |
− m1 |
, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
m + m |
2 |
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
T = |
2m1m2 |
|
g . |
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
m + m |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
Действие на блок обусловлено двумя |
||||||||
|
|
|
|
Рис. 1.13 |
силами натяжения нитей T |
и силой ре- |
|||||||||
|
|
|
|
акции со стороны оси вращения. Поэто- |
|||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
42 |
|
|
|
|
|
|
|
|
му по 3-му закону Ньютона сумма сил 2T уравновешивает силу упругости N , действующую со стороны оси на блок (ось блока неподвижна). Согласно третьему закону Ньютона сила упругости N численно равна силе давления на ось блока, значит:
N = 2T = 4m1m2 g . m1 + m2
Произведя вычисления, получим окончательно:
a = 9,81× 0,12 - 0,08 =1,96 м/с2, 0,12 + 0,08
N = 4 × 0,12 × 0,08 9,81 =1,88 Н. 0,12 + 0,08
Ответ: a = 1,96 м/с2, N = 1,88 Н.
Пример 8. На наклонной плоскости, составляющей с горизонтом угол α = 30° , находится тело массой m1 = 2,0 кг (см. рис. 1.14). Тело движется вверх по наклонной плоскости под действием груза массой m2 = 20 кг, соединенного с ним невесомой
нерастяжимой нитью. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость μ = 0,10 . Определить
ускорение, с которым движется тело, силу натяжения нити, а также силу давления на ось блока. Блок считать невесомым и вращающимся без трения.
Дано:
α = 30° , m1 = 2,0 кг, m2 = 20 кг, μ = 0,10 .
Найти: a , T , N1 .
Решение. На тело, движущееся по наклонной плоскости, дей-
= r
ствуют сила тяжести [3.2] Fm1 m1 g , сила натяжения нити T1 , си-
43
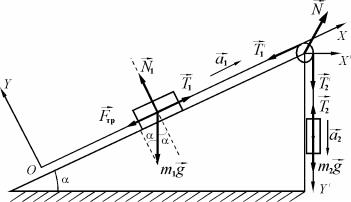
ла трения Fтр и сила реакции плоскости N1 . На груз m2 дейст-
r |
|
. Так как |
вуют сила тяжести Fm2 = m2 g и сила натяжения нити T2 |
||
нить невесома, трение на оси в блоке отсутствует, |
то T1 |
= T2 = T . |
Из нерастяжимости нити следует, что a1 = a2 = a . |
Выберем для |
|
тела m1 систему отсчёта XOY так, как указано на рис. 1.14.
Рис. 1.14
Тогда уравнение движения (второй закон Ньютона [2.1]) тела
в проекциях на оси OX и OY запишется так: |
|
||
T1x + N1x + Fm1x + Fтрx = m1ax , |
|
(1) |
|
T1y + N1y + Fm1y |
+ Fтрy = m1ay . |
|
(2) |
Учитывая знаки проекций, а также то, что T1x = T , |
N1x = 0 , |
||
Fm1x = −m1 g sin α , |
ay = 0 , Fтрx |
= −Fтр = −μN1 [2.5], |
ax = a , |
N1y = N1 , Fm1y = −m1 g cos α , получим: |
|
||
T − m1 sin α − μN1 = m1a , |
|
(3) |
|
N1 − m1 g cos α = 0 . |
|
(4) |
|
Для груза выберем систему |
координат X ′OY ′ . Уравнение |
||
движения груза m2 будет иметь вид: |
|
||
m2 g − T = m2 a . |
|
|
(5) |
|
44 |
|
|
Решив полученную систему уравнений (3) – (5) относительно a , получим:
a = |
|
g[m2 - m1 (sin a + m cos a)] |
» 8,4 м/с2. |
(6) |
|
|
|
|
|||
|
|
m1 + m2 |
|
||
Зная ускорение a , можно найти силу натяжения нити: |
|
||||
T = |
m1m2 g(1 + sin a + m cos a) |
» 28,2 Н. |
(7) |
||
|
|||||
|
|
m1 + m2 |
|
||
Так как по условию задачи масса блока не учитывается, то можно считать, что на него действуют только две силы натяжения
T1¢ и T2¢ со стороны нити и нормальная реакция опоры N со сто-
роны оси.
Под действием приложенных сил блок находится в равно-
весии: |
|
|
|
|
|
|
T1¢ + T2¢ + N = 0 . |
r |
|
r |
|
|
(8) |
|
|
|
|
|
||
Так как нить невесома, то |
T1¢ |
= |
T2¢ |
= T , а по третьему закону |
||
Ньютона модуль силы реакции опоры |
|
r |
численно равен силе |
|||
|
N |
|||||
давления на ось блока. Записав выражение (8) в проекциях на ось,
совпадающей с направлением силы |
N , получим выражение для |
|||||
силы давления: |
|
|
ö |
|
|
|
æ |
90 |
o |
- a |
|
|
|
N = 2T cosç |
|
÷ |
» 48 Н. |
|
||
|
|
|
|
|||
ç |
|
|
2 |
÷ |
|
|
è |
|
|
ø |
|
|
|
Ответ: a = 8,4 м/с2, T = 28,2 Н, |
N = 48 Н. |
|||||
Пример 9. На двух шнурах одинаковой длины, равной 0,80 м, подвешены два свинцовых шара массами 0,50 и 1,0 кг (рис. 1.15). Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол α = 60° , и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и неупругим. Определить энергию, израсходованную на деформацию шаров при ударе.
45
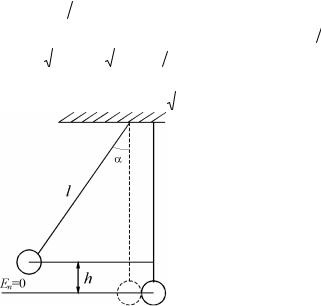
Дано:
m2 = 0,50 кг,
m2 = 1,0 кг,
α = 60° , l = 0,80 м.
Найти: h , Eд .
Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью υ . Закон сохранения импульса [4.1] имеет вид:
m1υ1 + m2 υ2 = (m1 + m2 )υ . |
(1) |
Здесь υ1 и υ2 — скорости шаров до удара. Скорость большего шара до удара равна нулю ( υ2 = 0 ). Скорость меньшего шара най-
дем, используя закон сохранения механической энергии [4.12]. При отклонении меньшего·шара на угол α (см. рис. 1.11) ему
сообщается потенциальная энергия [4.10], которая затем перехо-
дит |
в |
|
кинетическую поступательного |
движения |
|
|
[4.11]: |
|||||||||||
m gh = m υ2 2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
1 |
1 |
1 |
|
|
|
= l(1 − cos α)= 2l sin 2 (α 2), поэтому: |
|||||||||||
|
Из рисунка видно, что h |
|||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
υ1 = |
|
|
|
= 2 |
|
sin(α 2). |
|
|
|
|
|
|
|
(2) |
|||
|
|
|
2gh1 |
gl |
|
|
|
|
|
|
|
|||||||
|
Из уравнений (1) и (2) находим скорость шаров после удара: |
|||||||||||||||||
|
υ = mυ1 /(m1 + m2 ) = 2m1 |
|
|
sin(α / 2) /(m1 + m2 ) . |
|
|
|
(3) |
||||||||||
|
|
gl |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Кинетическая энергия, |
|
которой |
|||||||
|
|
|
|
|
|
|
|
|
обладают шары после удара, пере- |
|||||||||
|
|
|
|
|
|
|
|
|
ходит в потенциальную: |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(m + m |
2 |
)υ2 |
/ 2 = (m + m |
2 |
)gh ,(4) |
|||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
где h – высота поднятия шаров |
|||||||||
|
|
|
|
|
|
|
|
|
после столкновения. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Из (4) |
находим h = υ2 /(2g) , или |
||||||||
|
|
|
|
|
|
|
|
|
с учетом (3): |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
h = 2m2l sin |
2 (α / 2) /(m + m |
2 |
)2 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
Рис. 1.15 |
|
Окончательно: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
||
h = 2 × 0,502 × 0,80 × 0,25 = 0,044 м. (0,50 +1,0)2
При неупругом ударе шаров часть механической энергии расходуется на их деформацию. Энергия деформации DEд определяется разностью кинетических энергий до и после удара:
DE |
д |
=1/ 2m u2 |
-1/ 2(m + m |
2 |
)u2 . |
|||||
|
1 1 |
|
|
1 |
|
|
|
|||
Используя соотношения (2) и (3), получаем |
||||||||||
|
|
æ |
|
|
m1 |
|
ö |
|
2 |
|
DEд |
ç |
|
|
|
÷ |
|
|
|||
- m + m |
|
|
|
(a / 2) . |
||||||
= 2glm1 ç1 |
2 |
÷sin |
|
|||||||
|
|
è |
1 |
|
ø |
|
|
|
||
Подставляя числовые значения, находим |
||||||||||
DEд |
= 2 × 9,81× 0,80 × 0,50(1 - 0,50 1,5)× 0,25 =1,3 Дж. |
|||||||||
Ответ: h = 0,044 м, DEд |
=1,3 Дж. |
|||||||||
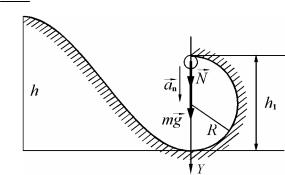
Пример 10. Небольшое тело массой m соскальзывает вниз по наклонному желобу, переходящему в «мертвую петлю» радиусом R = 0,20 м. С какой высоты h должно начать свое движение тело, чтобы не оторваться от желоба в верхней точке петли? Трением пренебречь.
Дано: R = 0,20 м. Найти: h .
Решение. Для решения задачи воспользуемся законом сохранения механической энергии [4.12]. Первым состоянием тела будем считать его состояние на высоте h (обладает лишь потенциальной энергией относительно нулевого уровня потенциальной энергии [4.10]), вторым – состояние в верхней точке петли (обладает и потенциальной, и кинетической [4.11]). Полная энергия тела в этих состояниях соответственно равна:
E1 = mgh , |
|
(1) |
||||
E |
2 |
= |
mu2 |
+ mgh . |
(2) |
|
|
|
|||||
|
|
|
|
1 |
|
|
2
С учетом того, что h1 = 2R , (2) перепишем в виде:
47
E2 = |
mυ2 |
+ mg2R . |
(3) |
|
2 |
||||
|
|
|
Согласно закону сохранения энергии, E1 = E2 . Приравнивая таким образом выражения (1) и (3), получим: mgh = m2υ2 + 2mgR ,
|
|
|
Рис. 1.16 |
|
|
|
|
|
|
|
|||
откуда искомая высота в момент начала движения: |
|
|||||
h = |
υ2 |
+ 2R . |
(4) |
|||
2g |
||||||
|
|
|
|
|
||
Чтобы найти скорость υ , рассмотрим силы, действующие на тело в верхней точке «петли». В общем случае на тело действуют две
|
|
|
|
|
|
r |
N . По |
силы: сила тяжести [3.2] F = mg и сила реакции желоба |
|||||||
второму закону Ньютона [2.1] получим: |
|
||||||
N + mg = |
mυ |
2 |
, |
|
(5) |
||
|
R |
|
|
||||
|
|
|
|
υ2 |
|
|
|
где величина |
|
– центростремительное (нормальное) уско- |
|||||
|
R |
||||||
|
|
|
|
|
|
|
|
рение [1.14] при движении тела по окружности радиуса R . |
|
||||||
Согласно условию задачи, требуется определить высоту h |
|||||||
для предельного случая, когда N = 0 . Тогда (5) примет вид: |
|
||||||
mg = |
mυ2 |
|
, |
|
|
|
|
R |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
откуда υ2 |
|
= gR . |
|
|
|||
|
|
|
|
|
|
48 |
|
Из (4), подставляя найденное соотношение и числовые значения, получим значение высоты h = 2,5R = 0,50 м.
Ответ: h = 0,50 м.
Пример 11. Молот массой m1 = 200 кг падает на болванку, масса m2 которой вместе с наковальней равна 2500 кг. Скорость молота в момент удара равна υ1 = 2,0 м/с. Найти: 1) кинетическую энергию E1 молота в момент удара; 2) энергию E2 , переданную
фундаменту; 3) энергию E , затраченную на деформацию болванки; 4) коэффициент полезного действия η (КПД) удара молота о
болванку. Удар молота о болванку рассматривать как неупругий.
Дано:
m1 = 200 кг, m2 = 2500 кг,
υ1 = 2,0 м/с.
Найти: E1 , E2 , E , η .
Решение. Кинетическую энергию [4.11] молота в момент удара найдем в виде:
E = |
m υ2 |
|
1 1 |
. |
|
|
||
1 |
2 |
|
|
|
|
Подставив значения m1 и υ1 и произведя вычисления, получим E1 = 400 Дж.
Чтобы определить энергию, переданную фундаменту, предварительно найдем скорость системы молот-болванка (с наковальней) непосредственно после удара. Для этого применим закон сохранения импульса [4.1], который в случае неупругого удара двух тел выражается следующим образом:
m1υ1 + m2 υ2 = (m1 + m2 )u , |
(1) |
где υ2 – скорость болванки (вместе с наковальней) перед ударом;
u – скорость молота и болванки (вместе с наковальней) непосредственно после удара. Так как болванка с наковальней до удара на-
49
ходилась в состоянии покоя, то υ2 = 0 . Так как удар неупругий, то
молот и болванка (с наковальней) движутся как одно целое, то есть с одинаковой скоростью u . Из (1) найдем эту скорость:
u = |
|
m1 |
υ1 . |
(2) |
|
m1 |
+ m2 |
||||
|
|
|
|||
В результате сопротивления фундамента скорость u |
быстро |
||||
гасится, а кинетическая энергия, которой обладает система молотболванка (с наковальней), передается фундаменту. Эту энергию находим в виде [4.11]:
E2 |
= |
m1 + m2 |
u 2 . |
|
|
|
||||
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
Используя выражение (2), получим: |
||||||||||
|
= |
|
|
m2 |
υ2 |
|
|
|
|
|
E2 |
|
|
1 |
1 |
|
, |
|
|
|
|
2(m1 + m2 ) |
|
|
|
|||||||
|
|
|
|
|
|
|||||
или, учитывая, что E = m υ2 |
2 , запишем: |
|||||||||
|
|
|
|
m1 |
|
|
1 |
1 |
1 |
|
E2 |
= |
|
|
|
E1 . |
|
|
(3) |
||
|
m1 |
+ m2 |
|
|
||||||
|
|
|
|
|
|
|
|
|||
Подставив в выражение (3) значения m1 , m2 , E1 и произведя вычисления, получим:
E2 = 29,6 Дж.
Молот до удара обладал энергией E1 ; E2 – энергия, передан-
ная фундаменту. Следовательно, при деформации болванки выделилась энергия:
E = E1 − E2 .
Подставив в это выражение числовые значения E1 и E2 , по-
лучим:
E = 370 Дж.
Назначение молота – путем ударов о болванку, находящуюся на наковальне, вызвать деформацию болванки; следовательно, энергию E следует считать полезной. КПД удара молота о бол-
50