МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И РОБОТОТЕХНИКИ

Кафедра «Системы автоматизированного проектирования»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту

по дисциплине

«Геометрическое моделирование»

Тема: «Получение реалистического изображения трехмерного объекта, представляющего собой полигональную сетку, его преобразование и проецирование»

Исполнитель: студентка гр. 107528

Клецкова Ю.В.

Руководитель: Сиденко Л.А.

Минск 2012

Содержание.

1. Описание объекта и получение геометрической модели. 4

2. Геометрические преобразования. 5

3. Проецирование. 7

4. Удаление невидимых линий. 15

5. Закраска изображения с учетом освещения. 16

6. Разработка интерфейса программы. 18

Заключение. 19

Литература. 20

Приложение. 21

Тестирование результатов работы программы. 21

Введение

При решении большинства задач в области автоматизированного конструирования и технологической подготовки производства надо иметь модель объекта проектирования. Модель объекта – некоторое абстрактное представление, удовлетворяющее условию адекватности этому объекту и позволяющее осуществлять его представление и обработку с помощью компьютера. Модель – набор данных, отображающих свойства объекта и совокупность отношений между этими данными.

В модель объекта, в зависимости от характера ее исполнения, может входить ряд разнообразных характеристик и параметров. Чаще всего модели объектов содержат данные о форме объекта, его размерах, допусках, применяемых материалах, механических, электрических, термодинамических и других характеристиках, способах обработки, стоимости, а также о микрогеометрии (шероховатость, отклонения формы, размеров). Для обработки модели в графических системах САПР существенным является не весь объем информации об объекте, а та часть, которая определяет его геометрию, т.е. формы, размеры, пространственное размещение объектов.

Описание объекта с точки зрения его геометрии называется геометрической моделью объекта. Но геометрическая модель может в себя включать еще и некоторую технологическую и вспомогательную информацию. Информация о геометрических характеристиках объекта используется не только для получения графического изображения, но и для расчетов различных характеристик объекта (например, по МКЭ), для подготовки программ для станков с ЧПУ. В традиционном процессе обмен информацией осуществляется на основе эскизных и рабочих чертежей с использованием нормативно-справочной и технической документации. В САПР этот обмен реализуется на основе внутримашинного представления объекта.

Под геометрическим моделированием понимают весь многоступенчатый процесс – от вербального (словесного) описания объекта в соответствии с поставленной задачей до получения внутримашинного представления объекта.

В системах геометрического моделирования могут обрабатываться 2-мерные и 3-хмерные объекты, которые в свою очередь могут быть аналитически описываемыми и неописываемыми. Аналитически неописываемые геометрические элементы, такие как кривые и поверхности произвольной формы, используются преимущественно при описании объектов в автомобиле-, самолета- и судостроении.

Все сказанное выше доказывает то, что трехмерное моделирование это одна из самых важных задач, решаемых в САПР сегодня.

1. Описание объекта и получение геометрической модели.

В разрабатываемой программе предлагается создать реалистичное изображение трехмерного объекта, состоящего из двух конечных элементов типа параллелепипеда и призмы (треугольная, треугольник правильный), объединенных по плоскости без проникновения.

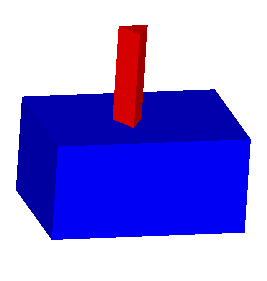
Рис.1. Реалистичное изображение трехмерного объекта.

В итоге в программе необходимо предусмотреть варианты соединения тел (впереди, сзади, сверху, снизу, слева, справа). При этом должна присутствовать возможность задания размеров тел (длина, высота, ширина параллелепипеда; высота и основание призмы ).

Над построенным таким образом объектом необходимо реализовать ряд геометрических преобразований, включающих в себя перемещение вдоль координатных осей, масштабирование, поворот вокруг координатных осей. Также в проекте должны присутствовать функции расширенного построения изображения объекта, то есть возможность построения ортографии (фронтальной, горизонтальной и профильной проекций), аксонометрии, косоугольной и перспективной проекциий.

Чтобы решить поставленную задачу необходимо получить трехмерную геометрическую модель выше описанного тела. Описание объекта с точки зрения его геометрии называется геометрической моделью объекта.

В данной работе я использую совокупность двух моделей: каркасной и поверхностной. В каркасной модели описываются вершины (их координаты) и грани (указатели на вершины). Это делается следующим образом:

V1={X1, Y1, Z1} – вершина, заданная координатами;

R1={ V1, V2,} - ребро, заданное двумя вершинами;

G1={V1, V2, V3, V4} – грань, заданная четырмя вершинами, где

V1 – V4 – это указатели на конкретные вершины.

Все координаты вершин заносятся соответственно в два массива для параллелепипеда pPar = new Point3[8] и для призмы pPr = new Point3[6].

Получение на экране каркасной модели осуществляется перебором всех граней, принадлежащих объекту, и последовательным отображением линий, соединяющих вершины, принадлежащих грани.

2. Геометрические преобразования.

К геометрическим преобразованиям любого объекта относятся перенос, масштабирование и поворот (относительно точки либо оси). Чтобы получить данные преобразования я перемножаю матрицы точек объекта на матрицы соответствующего преобразования , и . В итоге получаются матрицы новых точек объекта . Трехмерные преобразования представляются в виде матриц . Точка объекта записывается в однородных координатах как , где . Если же , то – . Точка, представленная в виде матрицы имеет вид:

.

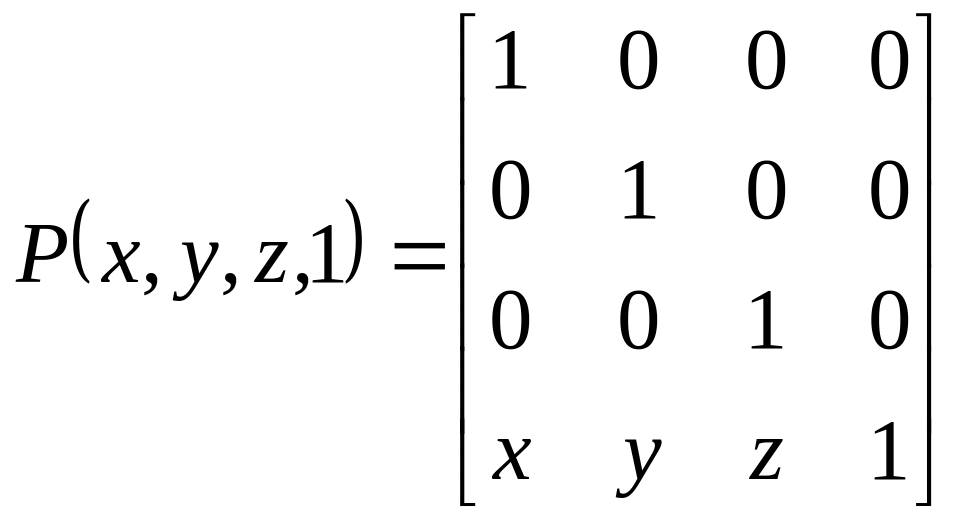Перенос:

Матрица трехмерного переноса представлена в виде:

, тогда .

dx- значение переноса относительно оси OX.

dy- значение переноса относительно оси OY.

dz- значение переноса относительно оси OZ.

Масштабирование:

Матрица трехмерного масштабирования представлена в виде:

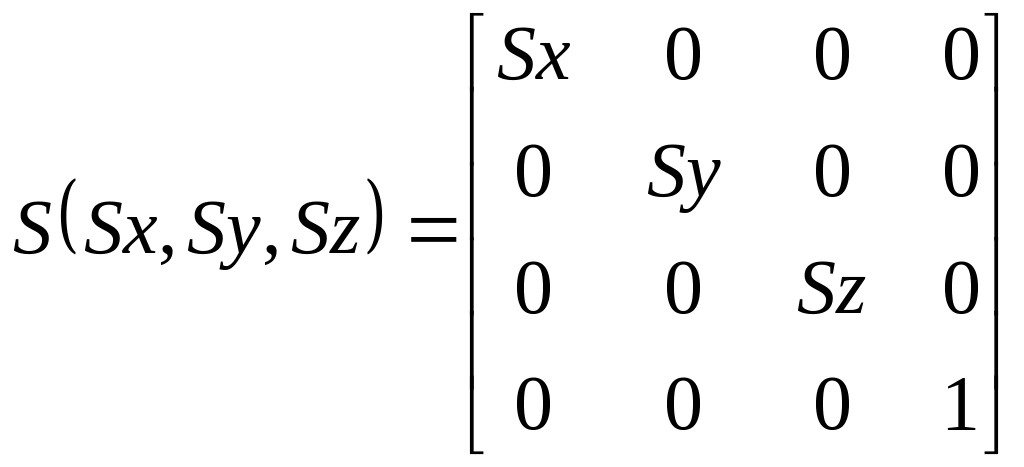, тогда .

sx- коэффициент масштабирования относительно оси OX.

sy- коэффициент масштабирования относительно оси OY.

sz- коэффициент масштабирования относительно оси OZ.

Поворот:

Матрица трехмерного поворота вокруг оси представлена в виде:

, тогда .

Матрица трехмерного поворота вокруг оси представлена в виде:

, тогда .

Матрица трехмерного поворота вокруг оси представлена в виде:

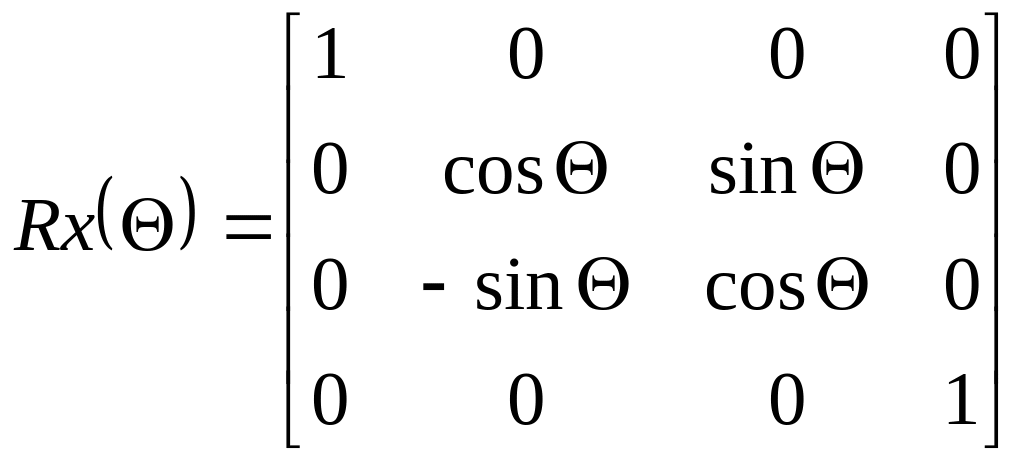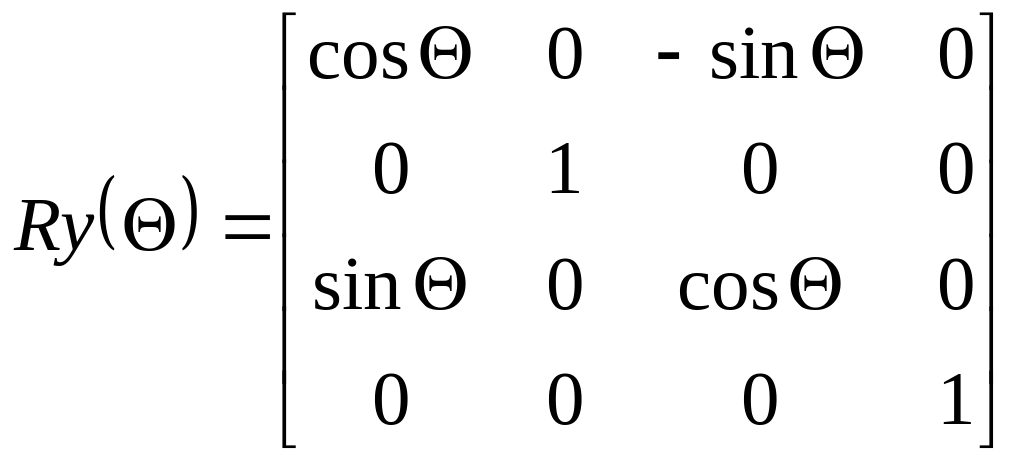, тогда .

Для извлечения новых координат точки после преобразования достаточно считать из матрицы три значения координат в последней строке.

В программе функция перемножения матриц является универсальной. Все зависит от того, какое преобразование нужно сделать с объектом (перенос, масштабирование или поворот). Она возвращает уже преобразованную матрицу точки C (объект перенесли, масштабировали или повернули):

public static Matrix Multiply(Matrix A, Matrix B)

{

Matrix C = new Matrix(A.Rows, B.Columns);

for (int i = 0; i < A.Rows; i++)

{

for (int j = 0; j < B.Columns; j++)

{

double tmp = C[i, j];

for (int k = 0; k < B.Rows; k++)

{

tmp += A[i, k] * B[k, j];

}

C[i, j] = tmp;

}

}

return C;

}

Эта же функцию я использую и при видовом преобразовании, тогда первым параметром является матрица видового преобразования, а вторым матрица собственно трехмерного преобразования.