§14. Формула Тейлора

Теорема. Пусть функция f(x) имеет в некоторой окрестности V(a) точки a производные до (n+1)-го порядка включительно. Пусть х – любая точка из V(a), p - произвольное положительное число. Тогда между точками а и х найдется такая точка с, что справедлива формула

, (1)

где , c(a;x) (или c(x;a)). (2)

Формула (1) называется формулой Тейлора с центром в точке а, R_n(x) - остаточный член формулы Тейлора в общей форме.

Доказательство.

Пусть (x;a) - многочлен n - порядка относительно х правой части формулы (1), т. е.

.

В силу условия (x;a) существует. Обозначим через R_n(x)=f(x)-(x;a). Тогда формула (1) будет доказана, если будет установлено, что R_n(x) имеет вид (2). Зафиксируем . Пустьx>a (для x<a доказательство аналогично). На отрезке [a;x] рассмотрим вспомогательную функцию (t):

, (3)

где , т. е..

Покажем, что (t) удовлетворяет условиям теоремы Ролля:

1. (t) непрерывна на [a;x],

2. (t) дифференцируема на (a;x),

3. ,

.

Значит, (a)=(x). Тогда на основании теоремы Ролля  c(a;x):  (с)=0. Дифференцируя (3), получим

.

Тогда  c(a;x): 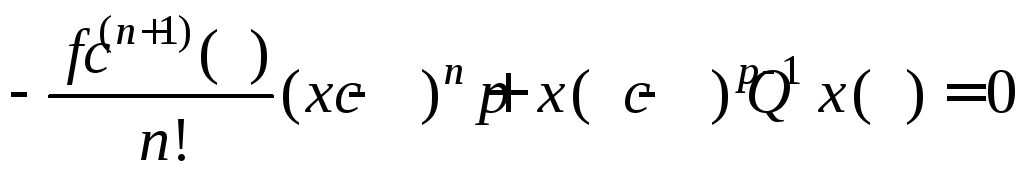.Следовательно,

. (4)

Тогда из (3), (4) следует

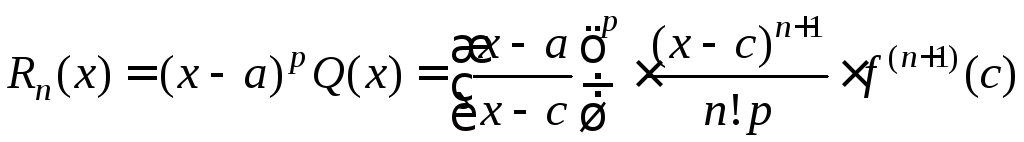, c(a;x).

Пример.1. Найти разложение по формуле Тейлора многочлена n-й степени

, , .

 fⁿ⁺¹(x)=Pⁿ⁺¹(x)=0 . Тогда R_n(x)=0 . Следовательно,

. 

Остаточный член формулы Тейлора в различных формах

Преобразуем формулу (2). Т. к. c(a;x), то существует такое число , 0<<1, что c=a+(x-a)  x-c=x-a-(x-a)=(x-a)(1-). Тогда

. (5)

Частные случаи.

1) p=n+1  или

, 0<<1. (6)

(6)– остаточный член в форме Лагранжа (наиболее употребительная форма).

2) p=1  . (7)

(7) – остаточный член в форме Коши.

Замечание 1. В формулах (6) и (7) , вообще говоря, различны, т. к. эти формулы получены из (2) при различных значениях р, а  зависит от р.

Замечание 2. В некоторых задачах важен лишь порядок R_n(x) относительно (x-a).

Из (6) 

 (8)

(8) - остаточный член в форме Пеано.

Замечание 3. С помощью формулы Тейлора можно производить приближенные вычисления f(x) с любой степенью точности: f(x)(x;a), погрешность равна R_n(x).

Замечание 4. Положим в (1) а=х₀, х-х₀=х, х=х₀+х, f(x₀+x)-f(x₀)=f(x₀)=y.

Тогда . Формула Лагранжаy=f(x)-f(x₀)=f (c)x является частным случаем формулы Тейлора и получается из нее при n=0. Действительно, при n=0

, 0<<1.

Формула Маклорена

Полагая в формулах (1), (6)-(8) а=0, получим

-

формула Маклорена;

- форма Лагранжа;

- форма Коши;

- форма Пеано.

Разложение некоторых элементарных функций по формуле Маклорена

1. y=f(x)=e^x, .

, . При x=0 f(0)=f⁽ⁿ⁾(0)=1 

,

где - форма Лагранжа;

- форма Коши;

- форма Пеано.

2. y=f(x)=sinx, .

,



,

.

3. y=f(x)=cosx, .

, 

,

.

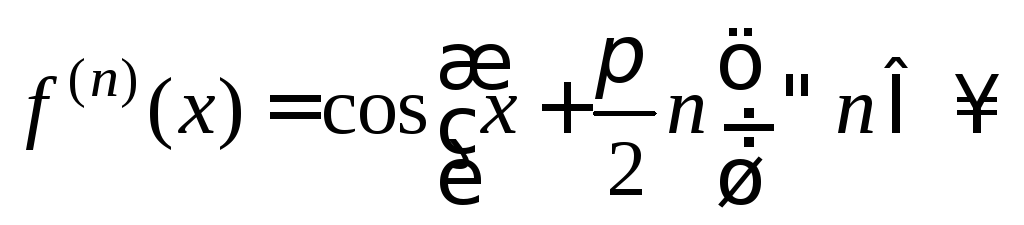4. y=f(x)=ln(1+x), .

. 

,

.

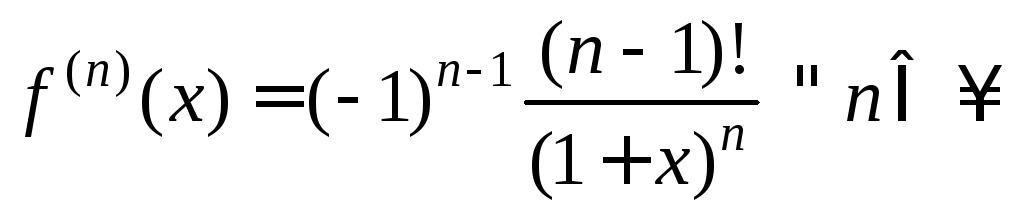5. y=f(x)=(1+x)^m, ,.

, ,

,

.

6. Пусть в случае 5 m=n  . Тогда

,



- бином Ньютона.

7. Пусть в случае 5 m=-1 

,

.

Положим здесь х=-х:

.

§15. Исследование функций с помощью производной

1. Условия постоянства, возрастания и убывания функций

Пусть f(x) определена в V(x₀).

Определение 1. Функция f называется возрастающей в точке x₀, если V(x₀,) точки x₀, такая, что

f(x)<f(x₀) при x<x₀ (x(x₀-, x₀),

f(x)>f(x₀) при x>x₀ (x(x₀, x₀+).

Определение 2. Функция f называется убывающей в точке x₀, если V(x₀,) точки x₀, такая, что

f(x)>f(x₀) при x<x₀ (x(x₀-, x₀),

f(x)<f(x₀) при x>x₀ (x(x₀, x₀+).

Теорема 1. Если функция f дифференцируема в точке x₀ и f (x₀)>0 (f(x₀)<0), то f возрастает (убывает) в точке x₀.

Доказательство.

По определению производной .

Пусть f (x₀)>0 (случай f (x₀)<0 доказывается аналогично). По определению предела функции по Коши получаем:

>0 (=f (x₀)) >0: x: |x-x₀|< выполнено 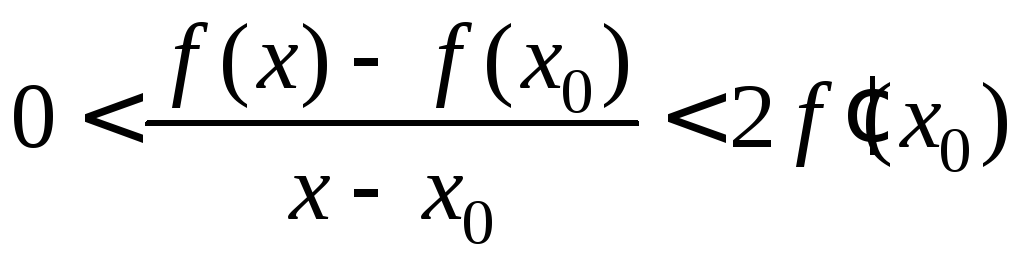  (1)

(1) выполнено .

Возьмем , т. е.x(x₀-, x₀)  x-x₀<0. Тогда из того, что  f(x)<f(x₀).

Возьмем , т. е.x(x₀, x₀+)  x-x₀>0. Тогда из того, что  f(x)>f(x₀).

На основании определения 1 функция f возрастает в точке x₀.

Замечание. Условие f (x₀)>0 (f (x₀)<0) не является необходимым для возрастания (убывания) функции в точке x₀. Т. е. из того, что f(x) возрастает (убывает)в точке x₀ не следует, что f (x₀)>0 (f (x₀)<0).

Пример.  f(x)=x³, . Рассмотрим точку x=0.

f (x)=3x², f (0)=0, но в точке х=0 функция возрастает. 

Теорема 2 (признак постоянства функции) Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Для того, чтобы f(x) была постоянной на [a;b] необходимо и достаточно, чтобы f(x)=0 x(a;b).

Следствие. Пусть f(x), g(x) определены и непрерывны на [a;b] и дифференцируемы на (a;b). Если f (x)=g (x) x(a;b), то f(x), g(x) отличаются друг от друга на постоянную.

Доказательство следует из теоремы 2 (применить для функции F(x)=f(x)-g(x)).

Теорема 3 (признак монотонности функции). Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Функция не убывает (не возрастает) на [a;b]  f (x)0 (f (x)0) на (a;b).

Доказательство.

1) Необходимость.

Пусть f не убывает на (случай невозрастания доказывается аналогично).

Тогда по определению x, x₀[a;b]: x<x₀  f(x) (x₀)  ,

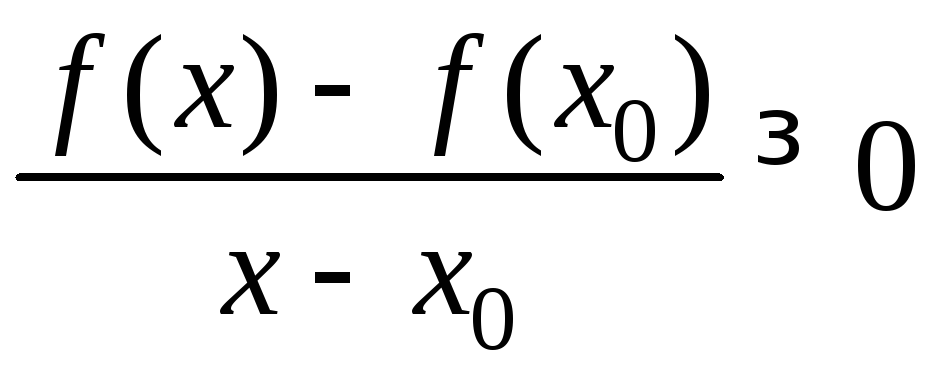x, x₀[a;b]: x>x₀  f(x) (x₀)  .

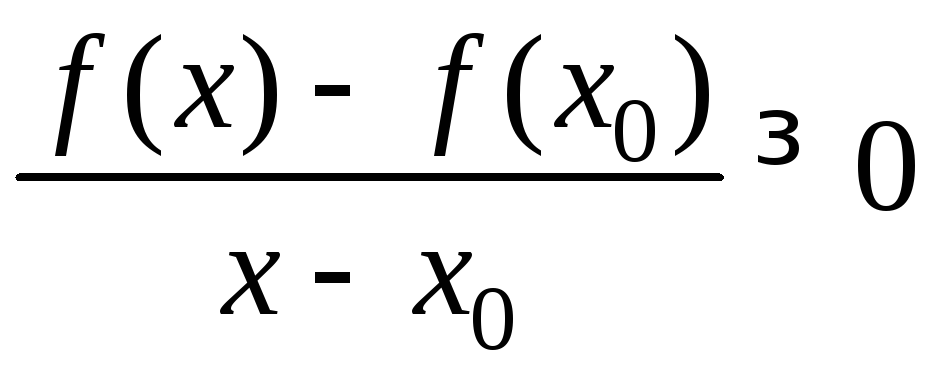Следовательно, 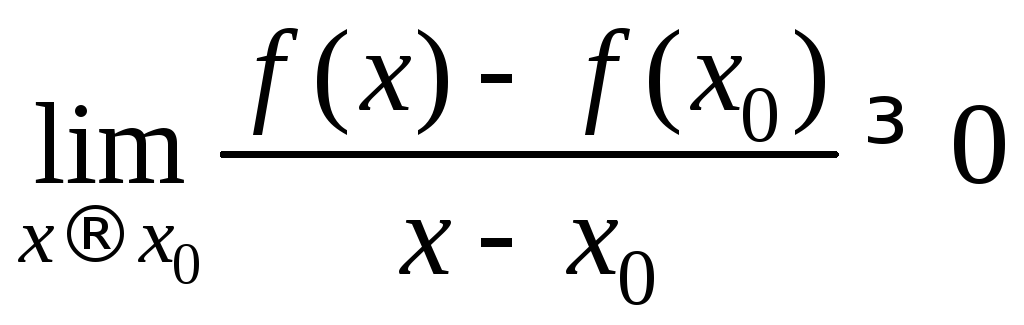, т. е.. Т. к. x₀[a;b] - произвольная точка, то необходимость доказана.

2) Достаточность.

Пусть f (x)0 на (a;b) (случай f (x)0 доказывается аналогично). Возьмем x₁, x₂[a;b]: x₁<x₂. К [x₁;x₂] применим теорему Лагранжа: с( x₁;x₂):

f(x₂)-f(x₁)=f (c)(x₂-x₁). Т. к. f (с)0, x₂-x₁>0, то f(x₂)-f(x₁)0. Т. е. f(x₂) f(x₁). По определению функция не убывает на [a;b].

Теорема 4. Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Если f (x)>0 (f(x)<0), то f возрастает (убывает) на (a;b).

Доказывается так же, как и п. 2) теоремы 3.

Замечание. Условие теоремы 4 является достаточным, а не необходимым. Например, функция y=x³ возрастает на , аf (0)=0.