
- •Дифференциальное исчисление функций одной переменной
- •§1. Производная
- •§2. Дифференцируемость и дифференциал функции
- •1. Дифференцируемость функции
- •2. Дифференциал функции
- •3. Применение дифференциала к приближённым вычислениям
- •§3. Геометрический смысл производной и дифференциала
- •1. Геометрический смысл производной
- •2. Геометрический смысл дифференциала
- •§4. Дифференцирование суммы, разности, произведения, частного
- •§6. Дифференцирование сложной функции.
- •1.Производная сложной функции.
- •2. Дифференциал сложной функции.
- •§7. Дифференцирование обратной функции.
- •§8. Производные основных элементарных функций.
- •§9. Производная показательно – степенной функции. Логарифмическое дифференцирование
- •§10 Производные высших порядков
- •§12. Основные теоремы дифференциального исчисления
- •§13. Раскрытие неопределенностей по правилу Лопиталя
- •§14. Формула Тейлора
- •§15. Исследование функций с помощью производной
- •1. Условия постоянства, возрастания и убывания функций
- •2. Экстремум функции
- •3. Нахождение наибольшего и наименьшего значений функции на отрезке.
- •4. Выпуклость функции.
- •5. Точки перегиба.
- •§ 16. Асимптоты графика функции
2. Дифференциал сложной функции.
Инвариантная форма дифференциала.
I.
Пусть y=f(x),
где х
– независимая переменная, дифференцируема
в точке х.
Следовательно,
существует
![]() ,
,![]() ,
т.к.х
– независимая переменная.
,
т.к.х
– независимая переменная.
![]() ,(1)
,(1)
![]() . (2)
. (2)
Таким образом, если х – независимая переменная, то имеем две формулы записи дифференциала (1) и (2).
II.
Пусть
y=f(x),
а x=g(t),
т.е. y=f(g(t)),
где t
– независимая переменная. Если g(t)
дифференцируема в точке t,
а y=f(x)
дифференцируема в соответствующей
точке x=g(t),
то сложная функция f(g(t))
дифференцируема в точке
t.
Т.к. t
– независимая переменная, то дифференциал
можно записать в виде:
![]() .
Тогда по теореме о производной сложной
функции
.
Тогда по теореме о производной сложной
функции
![]() ,
т.к.
,
т.к.
![]() .
.
Итак, ![]() .
Получили формулу записи дифференциала,
совпадающую с (2). Следовательно, формула
(2) инвариантна (неизменна).
.
Получили формулу записи дифференциала,
совпадающую с (2). Следовательно, формула
(2) инвариантна (неизменна).
Т.е. дифференциал функции y=f(x) записывается в форме (2) не зависимо от того, является ли х независимой переменной или функцией от какого–то аргумента.
Если x=g(t),
то
![]() .
Следовательно, форма (1) для дифференциала
сложной функции не подходит.
.
Следовательно, форма (1) для дифференциала
сложной функции не подходит.
§7. Дифференцирование обратной функции.
Теорема. Пусть
y=f(x)
непрерывна и монотонна в V(х0)
и дифференцируема в точке х0,
её производная
![]() .
Тогда вV(y0),
где
.
Тогда вV(y0),
где
![]() определена обратная функция
определена обратная функция![]() ,
дифференцируемая в точкеy0
и для её производной в этой точке
справедливо:
,
дифференцируемая в точкеy0
и для её производной в этой точке
справедливо:
 (1)
(1)
или
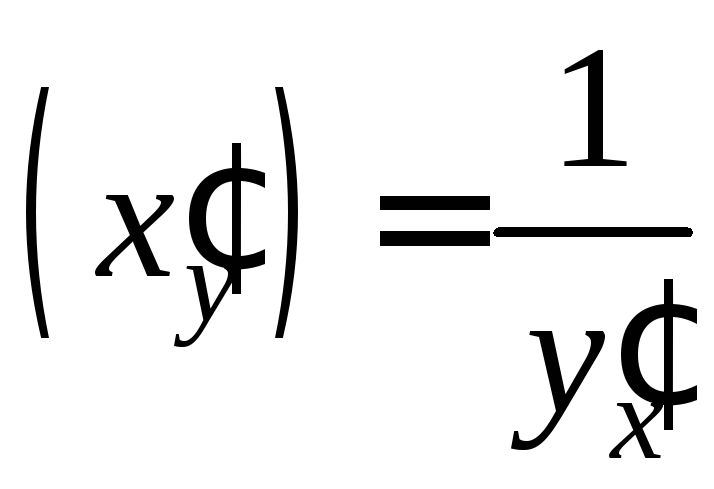 .
.
Доказательство.
![]() Т.к. f
строго монотонна и непрерывна в V(х0),
то в V(y0)
определена обратная функция, также
непрерывная и монотонная. Докажем, что
обратная функция
Т.к. f
строго монотонна и непрерывна в V(х0),
то в V(y0)
определена обратная функция, также
непрерывная и монотонная. Докажем, что
обратная функция
![]() дифференцируема в точкеy0
и справедливо (1).
дифференцируема в точкеy0
и справедливо (1).
Возьмём
![]() .
Значениюy0
аргумента обратной функции придадим
приращение
.
Значениюy0
аргумента обратной функции придадим
приращение
![]() .
Тогда обратная функция получит приращение
.
Тогда обратная функция получит приращение![]() .
.
Т.к.
![]() ,
то
,
то![]() .
Действительно, допустим противное:
.
Действительно, допустим противное:![]() .
Тогда
.
Тогда![]() .
Т.к.
.
Т.к.![]() - монотонная функция, то отсюда следует,
что
- монотонная функция, то отсюда следует,
что![]() .
Следовательно,
.
Следовательно,![]() - противоречит условию
- противоречит условию![]() .
.
Можно записать:
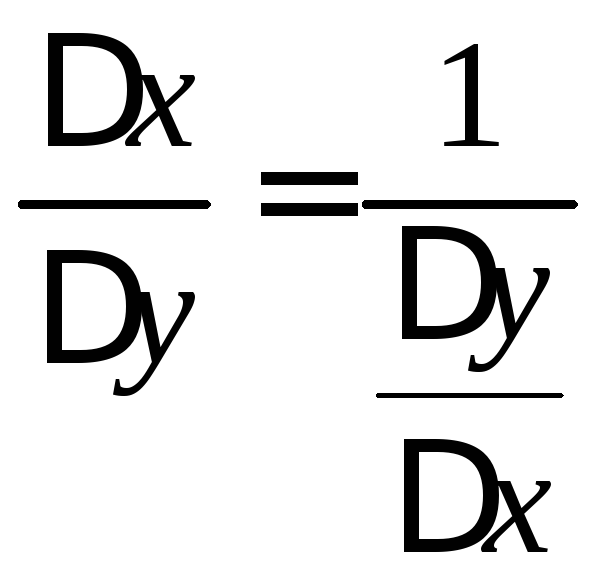 (2)
(2)
Пусть
![]() .
Тогда в силу непрерывности обратной
функции её приращение
.
Тогда в силу непрерывности обратной
функции её приращение![]() .
По условию
.
По условию![]()
![]() .
Следовательно,
.
Следовательно,
существует
![]() правой части (2):
правой части (2): .
Тогда существует и
.
Тогда существует и![]() левой
части при
левой
части при![]() (а, значит, и
(а, значит, и![]() ):
):

Переходя в равенстве
(2) к
![]() ,
получим (1).
,
получим (1).![]()
Замечание. Если
![]() и
и![]() вV(х0)
вV(х0)
![]() ,
то
,
то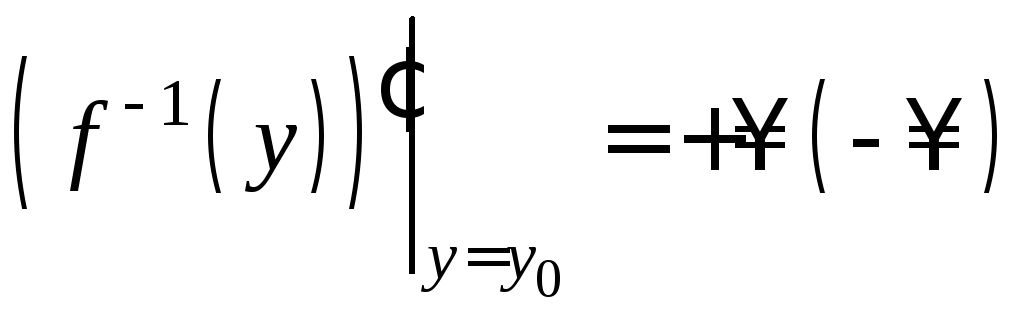 .
Если
.
Если![]() ,
то
,
то .
.
§8. Производные основных элементарных функций.
I.
Производная
степенной функции
y=f(x)=x,
![]() .
.
![]() Придадим произвольному
значению
Придадим произвольному
значению
![]() приращение
приращение![]() .
.
Тогда
![]() .
Разделим на
.
Разделим на![]() :
:
 ,
,
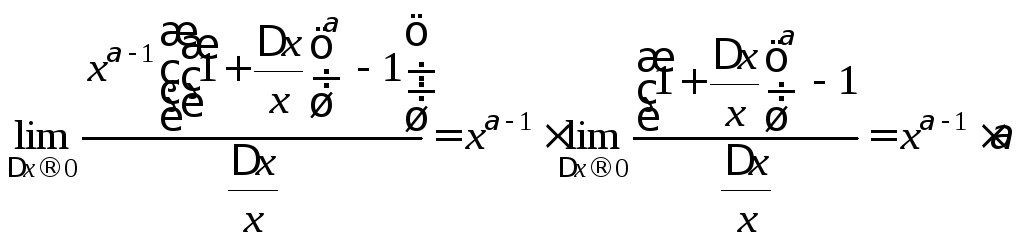 .
.
![]()
![]() - существует
- существует
![]() .
.![]()
![]()
![]() .
.
Частный случай:
![]() ,
,![]()
![]()
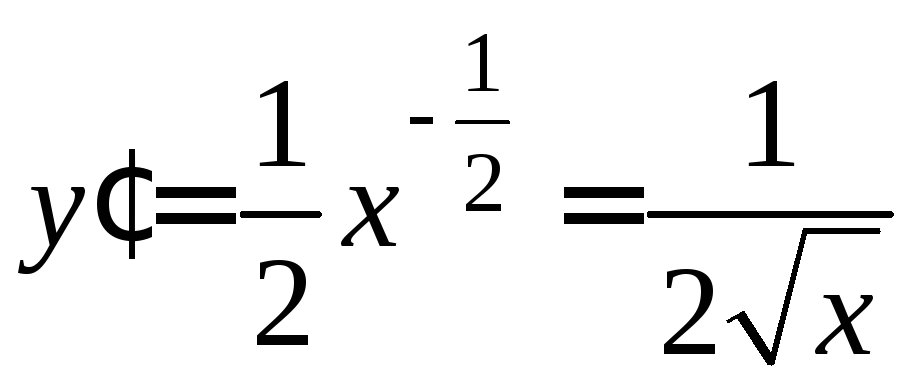 ,
,
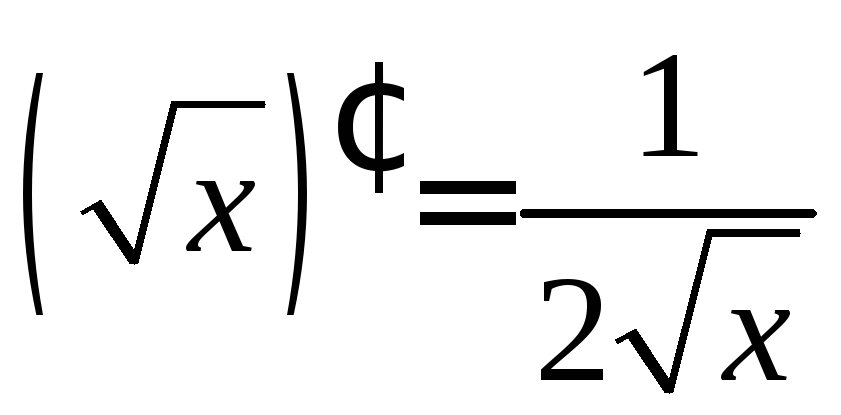 .
.
II.
Производная показательной функции:
y=f(x)=ax
![]() ,
,![]() .
.
![]() Выберем
Выберем
![]() ,
придадим приращение
,
придадим приращение![]() ,
тогда
,
тогда
![]() ,
,  ,
,
 ,
,
![]() .
.
![]()
![]()
![]() .
.
Частный случай:
a=e
![]()
![]() .
.
III.
Производная
логарифмической функции
![]()
![]() .
.
![]()
![]() .
Выберем
.
Выберем![]() ,
придадим приращение
,
придадим приращение![]() ,
тогда
,
тогда
 ,
,
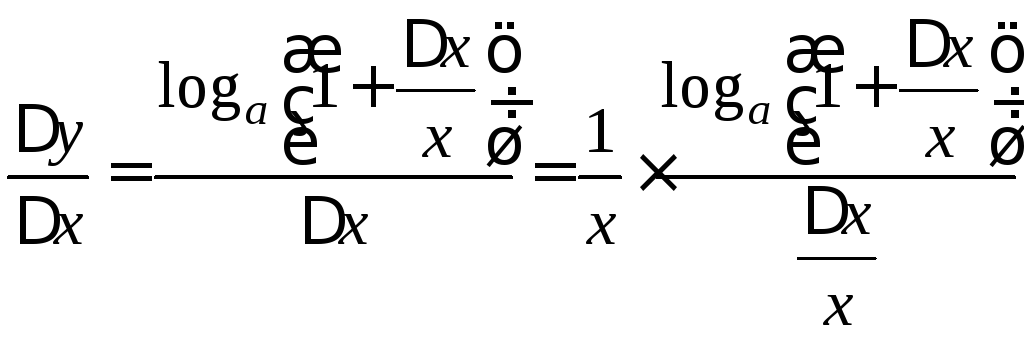 ,
,
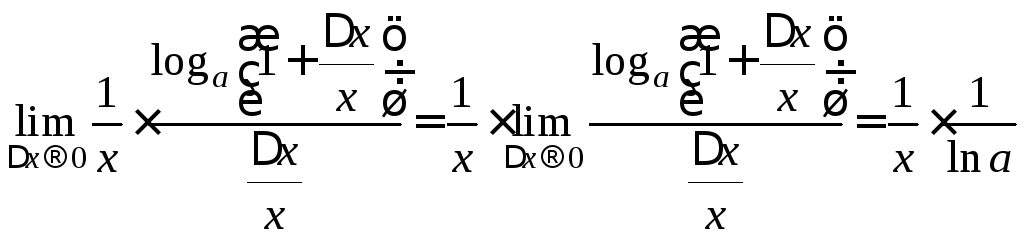 ,
,
![]()
![]() .
.
![]()
![]()
![]() .
.
Частный случай:
a=e
![]()
![]() .
.
IV. Производные тригонометрических функций.
1)
![]() ,
,![]() .
.
![]() Выберем
Выберем
![]() ,
придадим приращение
,
придадим приращение![]() ,
тогда
,
тогда
![]() ,
,
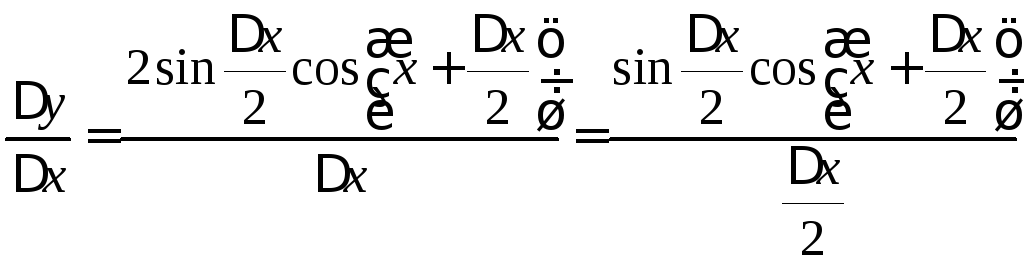 ,
,
![]()
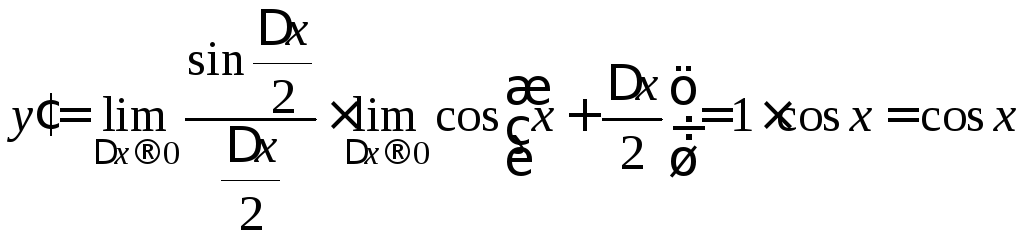 .
.
![]()
![]()
![]()
![]() .
.
2)
![]() ,
,![]() .
.

![]()
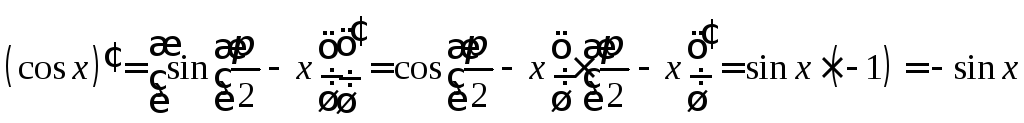 .
.
![]()
![]() .
.
3)
![]() ,
,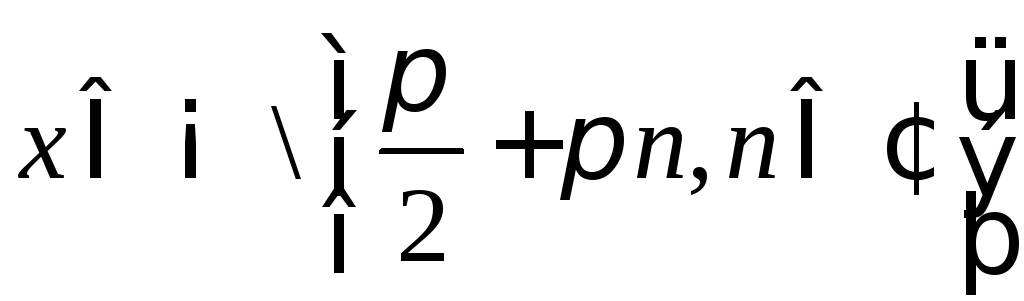 .
.
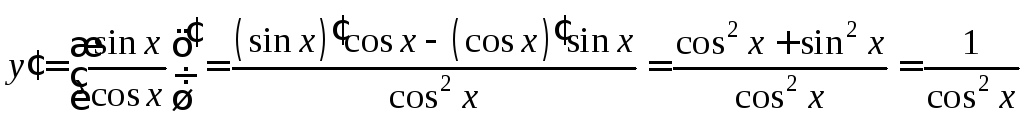 .
.
![]()
 .
.
4)
![]() ,
,![]() .
.
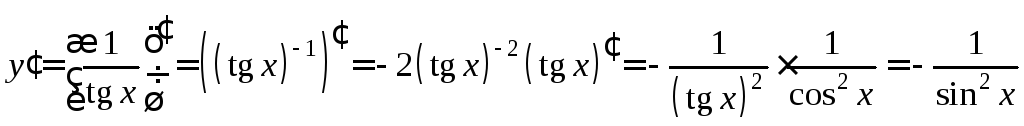 .
.
![]()
![]() .
.
V. Производные обратных тригонометрических функций.
1)
![]() ,
,![]() .
.
![]()
![]() на
на
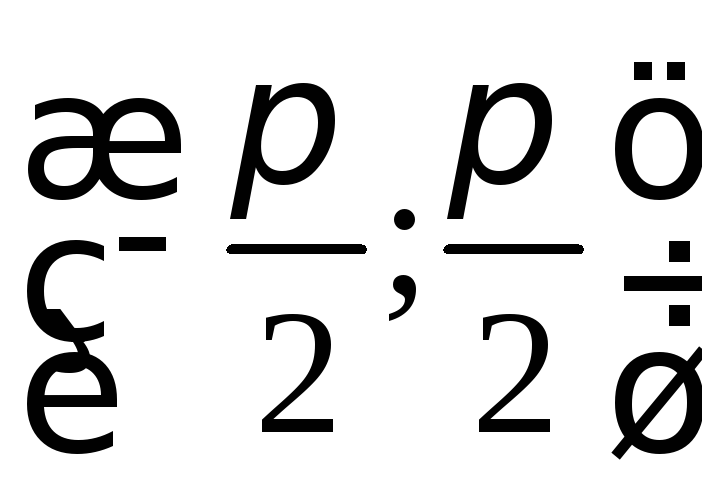 непрерывна, строго монотонна (возрастает),
дифференцируема:
непрерывна, строго монотонна (возрастает),
дифференцируема:![]() на
на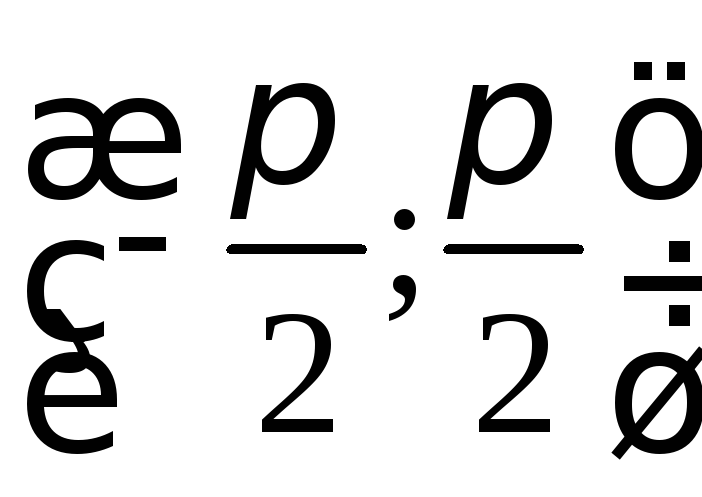 .
Следовательно,
.
Следовательно,![]() по правилу дифференцирования обратной
функции
по правилу дифференцирования обратной
функции
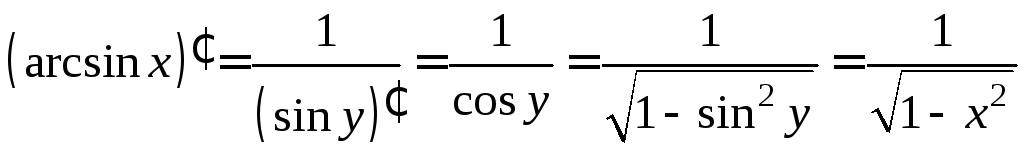
![]()
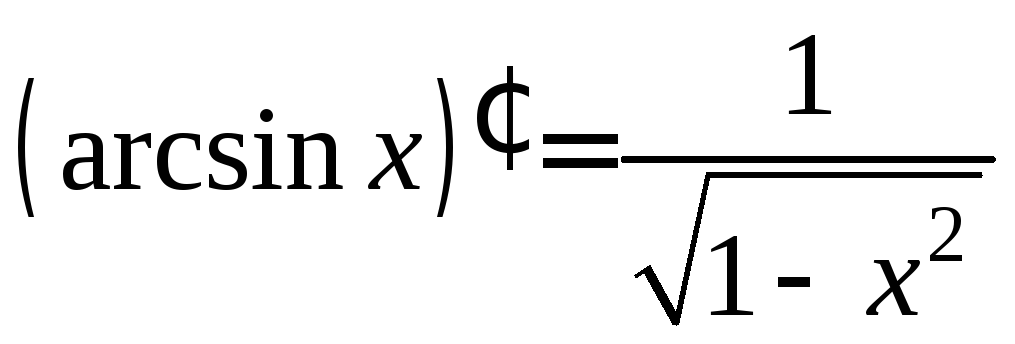
![]() .
.
Если
![]() ,
то
,
то![]()
![]()
![]() .
Тогда
.
Тогда![]()

![]()
2)
![]() ,
,![]() .
.
![]()
![]()
![]()

![]()

![]() .
.
![]()
![]()
3)
![]() ,
,![]() .
.
![]()
![]() - обратная функция
к
- обратная функция
к
![]() на
на .
.![]() непрерывна, строго монотонна,
дифференцируема и
непрерывна, строго монотонна,
дифференцируема и
![]()
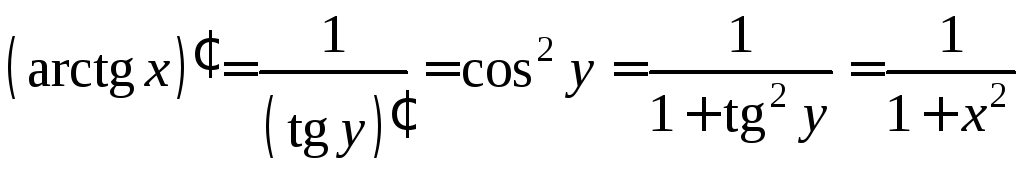
![]()
![]()
![]()
![]() .
.
4)
![]()
![]() .
.
 .
.
![]()
![]() .
.
VI. Производные гиперболических функций.
1)
 ,
,![]() .
.
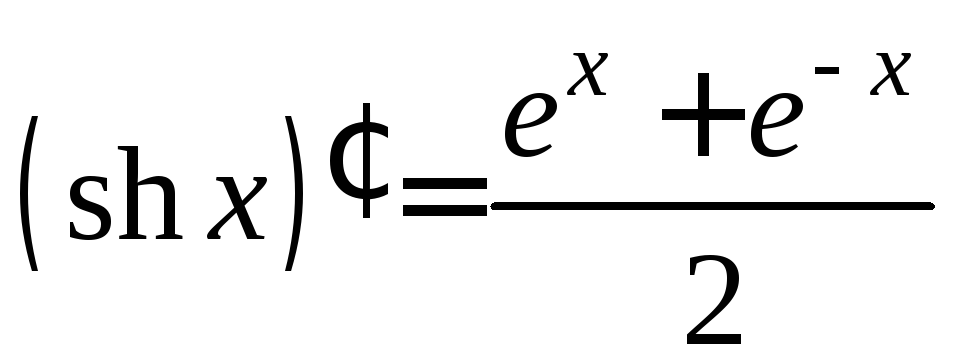 ,
,
![]()
![]()
![]()
![]() .
.
2)
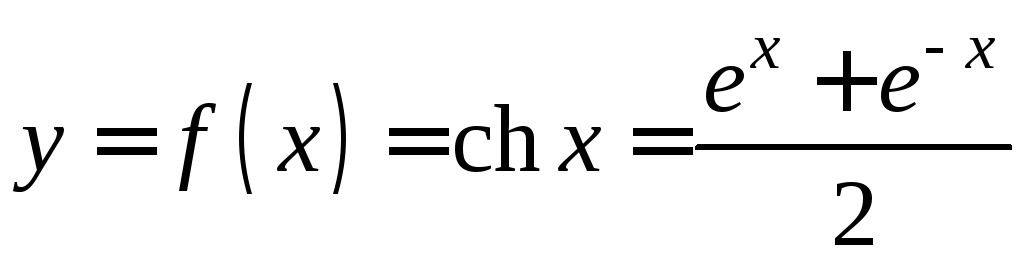 ,
,![]() .
.
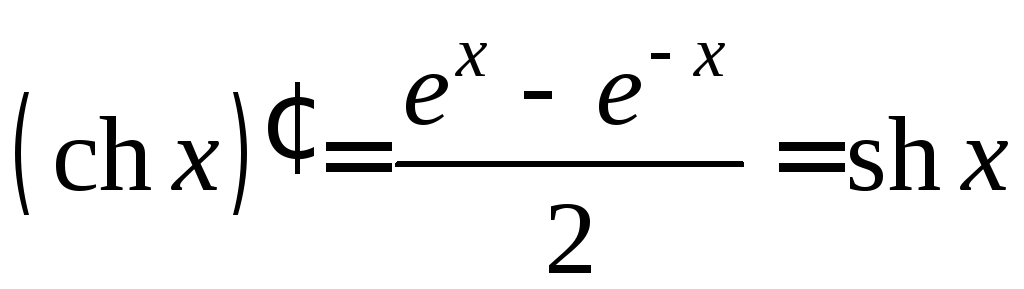
![]()
![]() .
.
3)
![]() ,
,![]() .
.
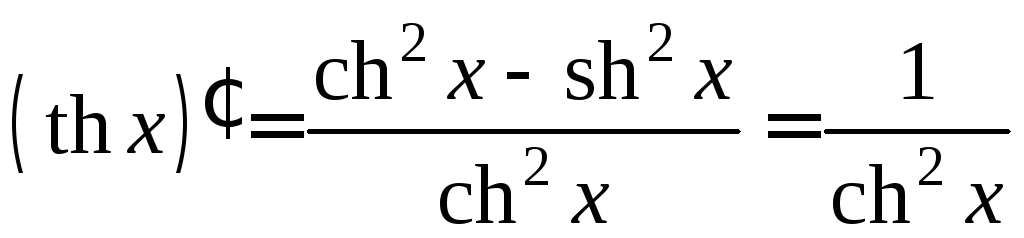 ,
,
![]()
![]() .
.
4)
![]() ,
,![]() \
\![]() .
.
 ,
,
![]()
![]() .
.
