§13. Раскрытие неопределенностей по правилу Лопиталя

1. Неопределенность .

Теорема 1. Пусть

1. f и g определены и дифференцируемы в ,;

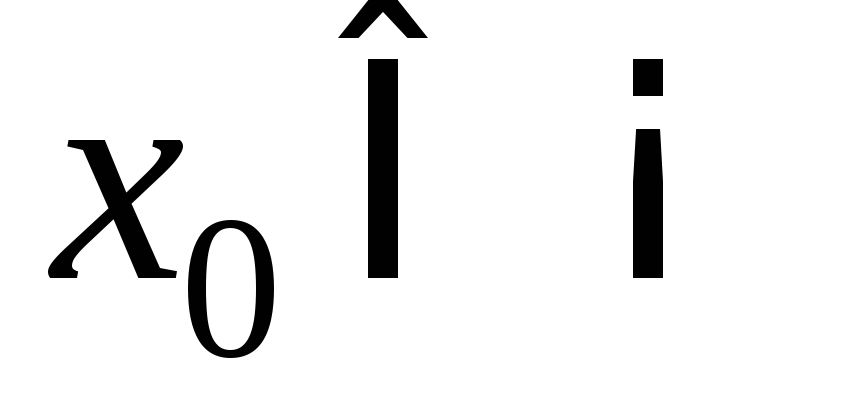2. g (x)0 ;

3. ;

4. существует конечный или бесконечный .

Тогда существует , т. е.. (1)

Доказательство.

Т. к. f и g дифференцируемы в , то они непрерывны в, кроме, быть может самой точкиx₀. Но если положить и , то доопределенные таким образом функции f и g непрерывны в точке x₀, т. е. в . Возьмем. Рассмотрим [x₀;x], если x>x₀ ([x;x₀], если x<x₀). Этот отрезок принадлежит . Функцииf и g на [x₀;x] ([x;x₀]) удовлетворяют условиям теоремы Коши. Тогда по этой теореме

, где с[x₀;x] (или с[x;x₀]).

Т. к. f(x₀)=g(x₀)=0, то . (2)

Пусть xx₀, тогда т. к. с[x₀;x] (или с[x;x₀]), то сx₀. По условию 4) . Т. к. существуетправой части равенства (2), то существует илевой части, равныйk. Переходя в (2) к , получим (1).

Рассмотрим случай, когда .

Теорема 2. Пусть

1. f и g определены и дифференцируемы в ;

2. g (x)0 ;

3. ;

4. существует конечный или бесконечный .

Тогда существует . (3)

Доказательство.

Используем теорему 1, применим замену . Положим,,.

1. Функции F и G определены и дифференцируемы в ,

, ;

2. G (t)0 на ;

3. , ;

4. . (4)

Т. о., функции F и G удовлетворяют условиям теоремы 1. Тогда

. (5)

С другой стороны, . (6)

Из (4)-(6) следует (3).

Из теорем 1 и 2 следует правило Лопиталя раскрытия неопределенностей : предел отношения двух бесконечно малых функций при хх₀ при выполнении условий 1)-4) теорем 1, 2 равен пределу прихх₀ отношения производных этих функций.

Пример 1.  . 

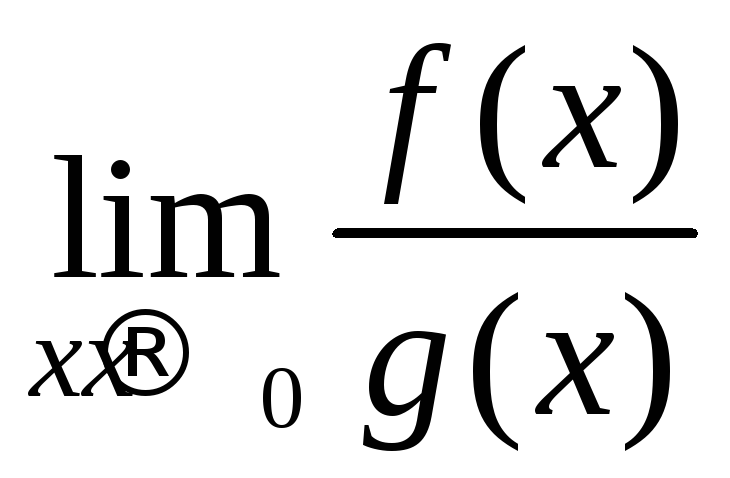Замечание 1. Если условие 4) теорем 1, 2 не выполнено, правило Лопиталя может не действовать: не существует, аможет существовать.

Пример 2.  ,х₀=0.

Для этих функций в выполнены условия 1)-3) теоремы 1. Ноне существует, т.к. не существует. Однако существует.

Замечание 2. Если производные f и g в окрестности удовлетворяют тем же условиям , что и сами функции (условия 1)-4)), то правило Лопиталя можно применять повторно.

Пример 3.



. 

2. Неопределенность .

Теорема 3. Пусть

1. f и g определены и дифференцируемы в ,;

2. g (x)0 ;

3. ;

4. существует конечный или бесконечный .

Тогда существует , т. е..

Из теоремы 3 следует правило Лопиталя раскрытия неопределенностей : предел отношения двух бесконечно больших функций при хх₀ при выполнении условий 1)-4) теоремы 3 равен пределу прихх₀ отношения производных этих функций.

Остаются в силе замечания 1, 2.

Пример 4.  Пусть a>1.

а) ;

б) .

Вывод. Показательная функция a^x (a>1) при растет быстрее, чем степеннаяxⁿ. Степенная функция xⁿ при растет быстрее, чем логарифмическаяlog_ax (a>1).

3. Неопределенности вида |0|, |-| сводятся к неопределенностям вида или 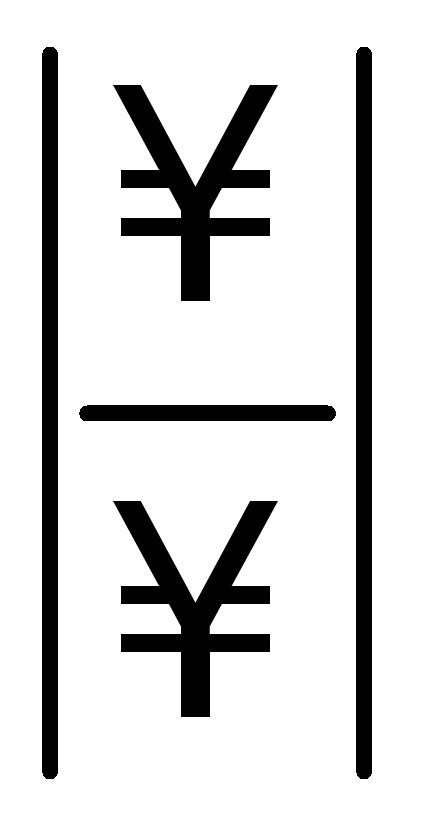: , |-| - привести к общему знаменателю.

Пример 5.  .

Пример 6. 

. 

IV. Неопределенности сводятся к |0|, а она к или .

Пример 7.  ;

.

Следовательно, .

Пример 8.  ;

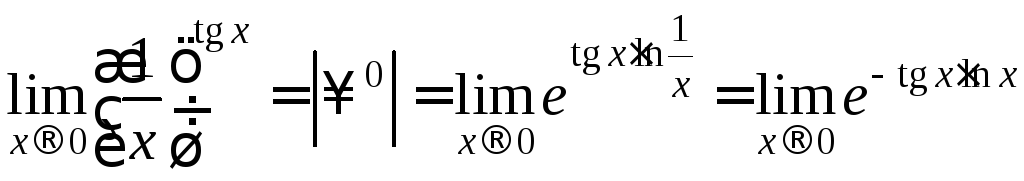Значит, .

Замечание. Важно в случае многократного применения правила Лопиталя не забывать каждый раз проверять, раскрыта ли неопределенность, иначе можно допустить ошибку.