2. Дифференциал функции

Пусть функция f(x) дифференцируема в точке х₀. Тогда приращение функции может быть представлена в виде суммы двух слагаемых.

1) - линейная функция относительно(содержитв первой степени),

2) - бесконечно малая функция высшего порядка, по сравнению спри.

Пусть . Покажем, что при.

.

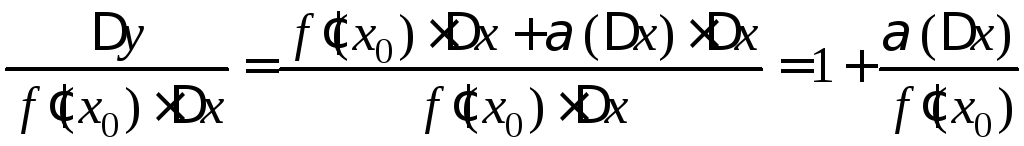Т. к. , то.

Говорят, что при является главной частью бесконечно малого приращения функции.

Определение 3. Дифференциалом функции f(x) в точке х₀ называется главная часть приращения функции, линейно зависящая от приращения аргумента . Обозначаетсяdy,

.

Если =0, то по определению=0.

Правило вычисления дифференциала следует из его определения. Дифференциал функции в точке х₀ равен произведению производной функции в этой точке на приращение аргумента.

Тогда (1) можем записать в виде

=,.

Пример. Найти приращение и дифференциал функции в произвольной точке.

 Пусть х- произвольное действительное число. Придадим х приращение , тогда

.

Значит, .

Рассмотрим функцию ,, то есть для независимого аргументах дифференциал и приращение совпадают: .

Определение 4. Дифференциалом независимой переменной х называется ее приращение :.

Тогда из определения дифференциала следует

.

Отсюда .

3. Применение дифференциала к приближённым вычислениям

При иdy0. Как было показано, при0 имеет место приближенное равенство, (в общем случае), которым пользуются при нахождении приближённых значений функций.

, .

§3. Геометрический смысл производной и дифференциала

1. Геометрический смысл производной

П

А

устьy=f(x) определена в и дифференцируема в некоторой внутренней точке. ПустьM₀(x₀;y₀) - некоторая точка графика функции, а М(х;у)- некоторая другая точка. Прямая М₀М называется секущей кривой y=f(x). Если оставить точку М₀ неподвижной, а точку М перемещать по кривой в направлении к М₀, то секущая будет поворачиваться вокруг М₀. При ММ₀ она будет стремиться к некоторому предельному положению М₀Т.

Определение. Касательной к кривой называется предельное положение секущей М₀М, когда ММ₀ по кривой.

х=х-х₀ .

Пусть секущая р, проходящая через точки М₀(х₀;y₀) и М(х₀+х;у₀+y) образует с положительным направлением оси Ох угол . ИзМ₀АМ

, (1)

т.е. =(x). Если х0, то ММ₀ по графику функции, и y0. Следовательно, секущая будет поворачиваться, и угол будет изменяться. Так как arctgx - непрерывная функция то

.

То есть существует правой части (1). Значит, существует илевой части, т.е. существует, и имеет место равенство. Следовательно, существует предельное положение угла, которое обозначим через ₀, т.е существует предельное положение М₀Т секущей М₀М при ММ₀. Следовательно, М₀Т- касательная к графику у=f(x) в точке М₀ и

.

Геометрический смысл производной состоит в следующем: производная функции f(x) в точке х₀ равна угловому коэффициенту касательной к кривой y=f(x) в точке (х₀;f(x₀)) (равна тангенсу угла наклона касательной к положительному направлению оси Ох)

Таким образом доказана

Теорема. Если функция f дифференцируема в точке х₀ (существует конечная производная ), то график этой функции имеет касательную, угловой коэффициент которой равен.

Замечание. 1) Если =0, то касательная к кривой в точкех₀ параллельна оси Ох (tg=0=0).

2) Если = tg₀= , то касательная к графику перпендикулярна оси Ох (функция не дифференцируема в точке х₀, а касательная существует).

3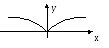) Может быть, чтоне существует , а касательная перпендикулярна оси Ох.

Пример. - не дифференцируема в точкех=0. Прямая х=0 (ось Оy) – касательная к графику в точке х₀=0.