2. Геометрический смысл дифференциала

Из рисунка: из М₀АВ .

Геометрический смысл дифференциала: дифференциал функции y=f(x) в точке х₀- это приращение ординаты точки касательной к графику функции в точке M₀(x₀;y₀), соответствующее приращению аргумента х.

3. Уравнение касательной и нормали к графику функции y=f(x)

Известно, что всякая прямая не параллельная оси Оу, проходящая через точку M₀(x₀;y₀), имеет уравнение .

Пустьf(x) дифференцируема в точке х₀. Следовательно, график функции имеет в точке (x₀;y₀) касательную, угловой коэффициент которой . Тогдауравнение касательной имеет вид

.

Прямая, проходящая через точку M₀(x₀;y₀) и перпендикулярная к касательной, называется нормалью к графику функции f в точке M₀(x₀;y₀). Т.к. коэффициенты перпендикулярных прямых k₁ и k₂, связаны соотношением , то,,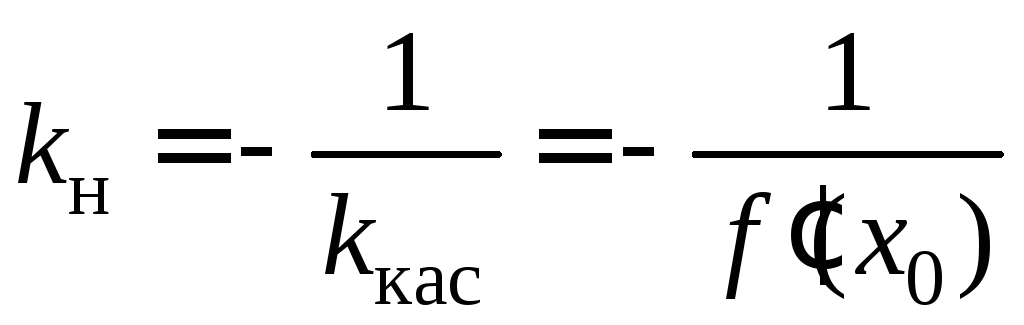 и, значит, уравнение нормали имеет вид

.

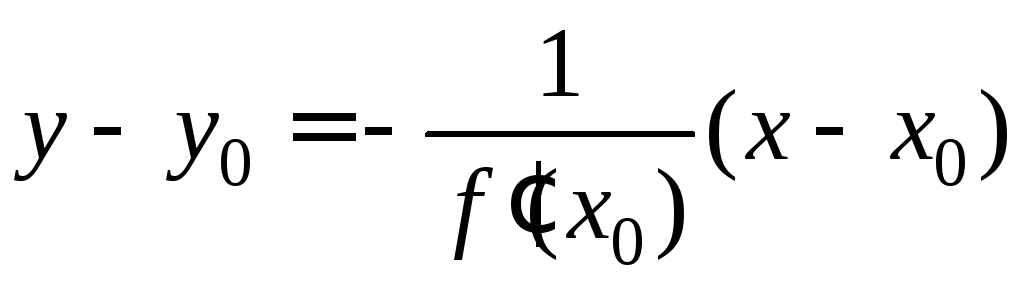§4. Дифференцирование суммы, разности, произведения, частного

Теорема 1. Если функции u=u(x) и v=v(x) дифференцируемы в точке х, то в этой точке дифференцируемы их сумма, произведение и (при условии, что ) частное, при этом справедливы равенства

, (1)

, (2)

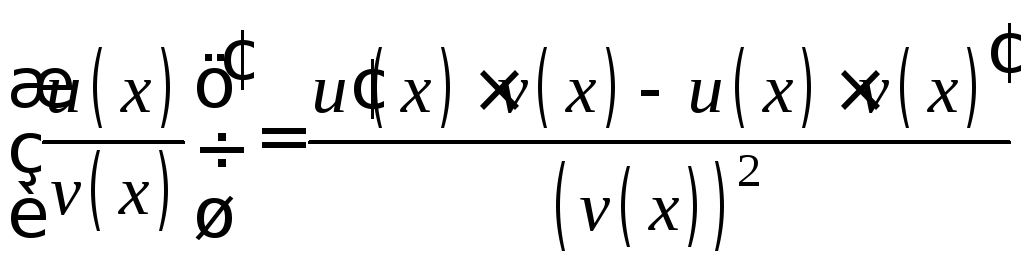. (3)

Доказательство.

1) Пусть . Придадим переменнойх приращение . Тогда функцииu и v получат приращения u и v соответственно. Тогда

,

. (4)

Пусть , так какu и v дифференцируемы в точке х, то существует и существует. Следовательно, существует правой части равенства (4): 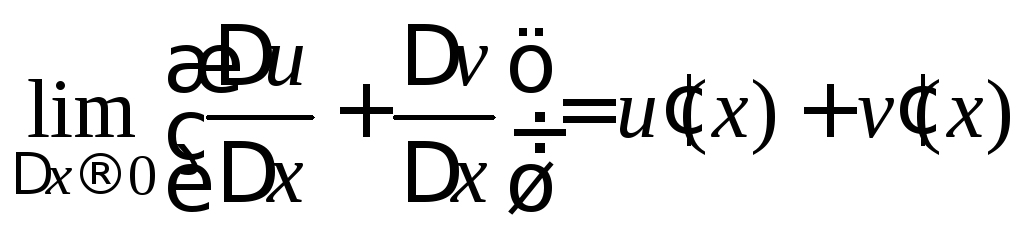. Значит, и существуети левой части .

Переходя в (4) к , получим .

2) Пусть y=u(x)v(x). Придадим точке х приращение . Функцииu=u(x) и v=v(x) получат приращения . Тогда

,

. (5)

Пусть . Так какu(x) и v(x) дифференцируемы в точке х, то существуети существует. Так как функцияu(x) дифференцируема в точке х, то она непрерывна в этой точке, значит, Поэтому существует

.

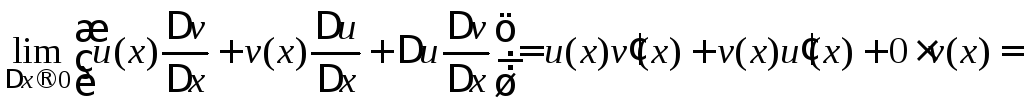
Так как существует правой части равенства (5), то существует и левой части, то есть существует . Переходя в (5) к получим

.

Замечание. Утверждения о дифференцируемости суммы и произведения справедливы для любого конечного числа функций.

Например .

Следствие 1. Если u(x) дифференцируема в точке х, а , то функцияy=Cu(x) также дифференцируема в точке х и (следует из формулы (2) при).

Следствие 2. Если функции u=u(x) и v=v(x) дифференцируемы в точке х, то в точке х дифференцируема их разность y=u(x)-v(x), причем (следует из формулы 1 и следствия 1).

Следствие 3. 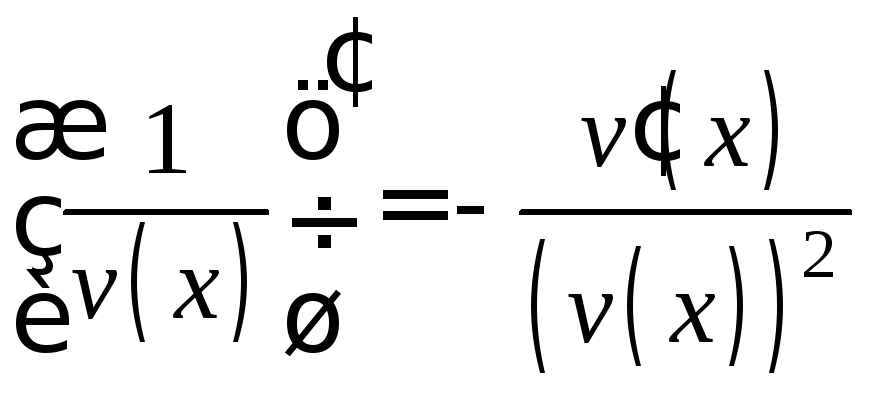(следует из формулы 3 при u(x)=1).

Теорема 1 справедлива как для точки, так и для промежутков. Кроме того, она переносится и на дифференциалы функций.

Теорема 2. Пусть u(x) и v(x) дифференцируемы в точке х. Тогда

,

,

,

.

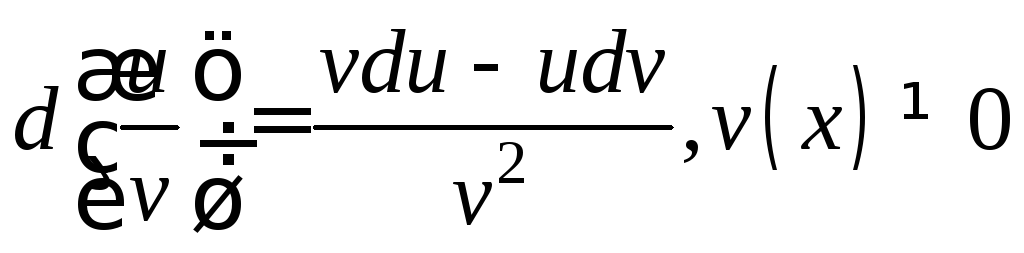Доказательство.

Например, для произведения:

.

§6. Дифференцирование сложной функции.

1.Производная сложной функции.

Теорема 1. Если функция t=(x) дифференцируема в точке х₀, а функция y=f(t) дифференцируема в точке , то сложная функцияy=f((x)) дифференцируема в точке х_0, и для производной в этой точке имеет место формула:

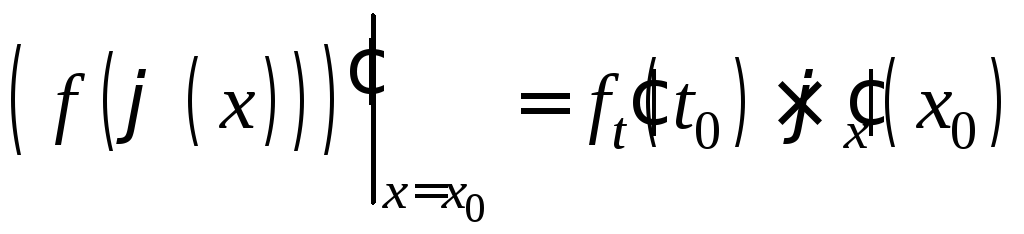(1)

(кратко:).

Доказательство.

По условию - сложная функция, непрерывная в точкех₀. Следовательно, она определена в некоторой окрестности точки х₀ V(х₀).

Придадим точке х₀ приращение:. Тогда функцияt=(x) получит приращение . Но тогда и функция y=f(t) в точке получит приращение. По условию y=f(t) дифференцируема в , значит, её приращение можно представить в виде:

, (2)

где .

Переменной х₀ мы дали приращение . В этом случае приращение функции(x) может быть равно 0. Если , тои равенство (2) не теряет смысла.

Обе части (2) разделим на .

(3)

Пусть . Т.к.t=(x) дифференцируема в точке х₀, то . Т.к.(x) дифференцируема в точке х₀ , то она непрерывна в точке х₀, т.е. . Значит, правая часть (3) имеет предел при, равный

.

Следовательно, существует и левой части:.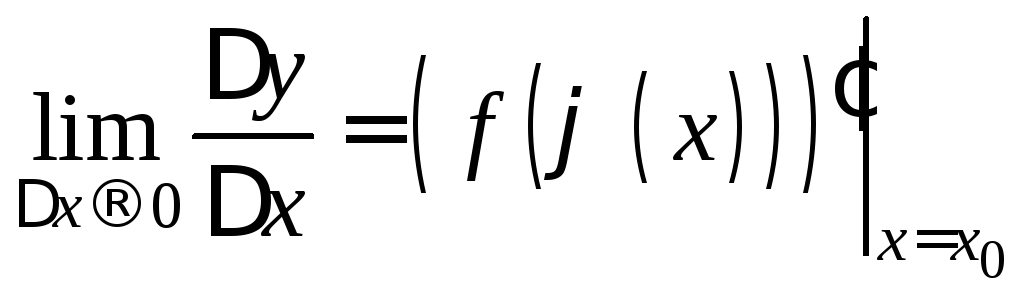

И выполнено

.

Замечание. , где , .