4. Корреляционная теория случайных последовательностей

В этом разделе мы рассмотрим применение корреляционной теории к случайным последовательностям, поскольку именно с последовательностями, то есть с отсчетами процесса в фиксированные моменты времени, исследователю чаще всего приходится иметь дело на практике. Сначала дадим ряд определений.

Случайная последовательность стационарна в узком смысле, если для всех ее конечномерных распределений и для любого k выполняется равенство

,

где m_i – номера отсчетов последовательности. Это определение абсолютно аналогично определению стационарной случайной функции (3.2). Случайная последовательность стационарна в широком смысле, если соответствующая ей автокорреляционная последовательность зависит только от сдвига индекса, то есть

и конечна при n = 0, то есть . При этом, очевидно, B[–n] = B^*[n]. Данное определение аналогично определению стационарной в широком смысле случайной функции, данному нами в конце п. 3.2.

По аналогии с определением эргодичности (3.8) случайной функции введем определение эргодичности для случайной последовательности. Случайная последовательность называется эргодической, если выполняется равенство

.

Критерий Слуцкого (3.7), записанный для случайной последовательности, выглядит следующим образом:

.

(4.12)

На практике чаще всего случайная последовательность представляет собой эквидистантную выборку случайного процесса с интервалом дискретизации t. В этом случае спектральная плотность интенсивности может быть определена как дискретно-временное преобразование Фурье (ДВПФ) автокорреляционной последовательности:

;

(4.13)

соответственно

.

(4.14)

Для чисто действительных случайных последовательностей B[–n] = B[n], поэтому выражения (4.13) и (4.14) упрощаются:

, .

Так же, как и для случайной функции, спектральную плотность интенсивности случайной последовательности можно выразить через ДВПФ самой последовательности:

.

(4.15)

Это выражение доказывается аналогично соотношению (4.7) и эквивалентно (4.13). Заметим, что корреляционная последовательность, так же, как и сама случайная последовательность, является выборкой корреляционной функции, то есть

.

Возникает вопрос, всегда ли по автокорреляциооной последовательности B[m] можно восстановить функцию автокорреляции B(). Для ответа на этот вопрос введем дискретизированную функцию автокорреляции

.

Соответствующая этой функции спектральная плотность интенсивности совпадает с ДВПФ автокорреляционной функции B():

.

С другой стороны, B_D() может быть представлена в виде произведения исходной функции B() на дискретизирующую последовательность (t), то есть

.

Из этой формулы и теоремы о свертке следует, что ДВПФ функции автокорреляции G_t(j) равно свертке спектральной плотности интенсивности процесса G(j) со спектром дискретизирующей пос­ле­до­ва­тель­но­сти (t):

.

(4.16)

Поскольку (t) – периодическая функция времени, ее мож­но разложить в ряд Фурье, коэф­фи­ци­ен­ты которого равны

,

и записать ее спектральную плотность в виде

.

Здесь – циклическая частота дискретизации. Подставив полученное выражение в формулу (4.16) и пользуясь фильтрующим свойством -функции, получим связь ДВПФ автокорреляционной последовательности со спектральной плотностью интенсивности процесса:

.

Таким образом, ДВПФ G_t(j) автокорреляционной последовательности представляет собой сумму (наложение) сдви­ну­тых на 2/t копий спектральной плотности интенсивности процесса. Если функция G(j) ограничена частотой _max (то есть G(|| > _max) = 0), а циклическая частота дискретизации _d удовлетворяет условию Найквиста:

,

(4.17)

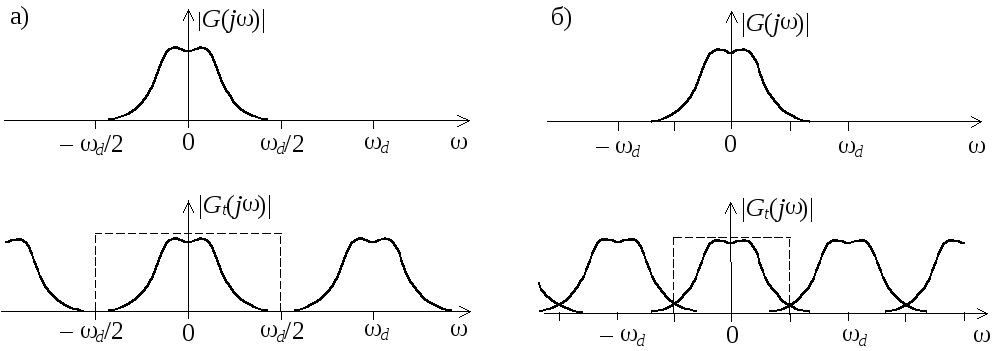
то копии функций G(j) при наложении не перекрываются, как это показано на рис. 4.2, а. В этом случае на интервале частот –_d/2 <  < _d/2 ДВПФ (4.13) полностью совпадает со спектральной плотностью интенсивности исследуемого случайного процесса и его функция автокорреляции может быть восстановлена по своим отсчетам с помощью обратного преобразования Фурье (4.14), вычисленного в пределах [–_d/2, _d/2]. Случай, когда условие (4.17) не выполняется, показан на рис. 4.2, б.

Рис. 4.2. Наложение спектров при дискретизации случайного процесса