4.1. Статусные Сообщения и Сброс.

Статусное сообщение информирует нас, каково текущее состояние автомата. Можно представить, что есть специальный символ, в ответ на который автомат выдает текущее состояние и остается в нем. Мы говорим, что статусное сообщение надежно, если оно гарантированно правильно работает в автомате B, т.е. выдает текущее состояние, не меняя его. Тогда тестовая последовательность может быть получена построением эйлерова пути для автомата A и применим в каждой вершине статусное сообщение. После этого можно узнать, подобен ли B A. Если статусное сообщение недостоверное, тогда тестовая последовательность строится, применяя статусное сообщение дважды, каждый раз как автомат переходит в новое состояние, т.е. каждый раз, когда переходим в новую вершину применяем дважды и один раз в остальных случаях.

Например, рассмотрим автомат A на рис.1 с начальным состоянием . Тогда эйлеров путь получается входной последовательностью x=ababab. Пусть s это статусное сообщение, тогда при надежном статусном сообщении x=sasbsasbsasbs, при ненадежном же x=ssasbssasbssasbs.

Мы говорим, что автомат A имеет возможность сброса, если через входной символ r можно попасть в начальное состояние из любого другого состояния, т.е. 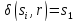, для любого 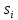. Говорится, что сброс надежен, если он гарантированно правильно работает в автомате B, т.е. 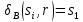, для любого , иначе ненадежно.

Для автоматов с надежным сбросом существует полиномный алгоритм построения тестовой последовательности. Пусть 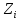, i=1,….,n семейство разделяющих последовательностей. Для каждого состояния мы имеем часть тестовой последовательности. Сначала, строим остовное дерево (методом поиска в ширину) диаграммы переходов автомата-эталона A и проверяем подобен ли B A. Мы проверяем состояния по алгоритму поиска в ширину и ребра (переходы) ведущие к вершинам (состояниям). Для каждого состояния есть часть тестовой последовательности, которая действует следующим образом для каждого члена : сначала, она переведет автомат в через r, затем подаст входную последовательность (скажем 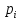) соответствующая пути в дереве от корня 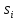до и потом применит разделяющую последовательность из . Если же автомат B пройдет этот тест для всех членов , мы узнаем, что B имеет состояние подобное 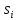, а именно состояние, полученное входной последовательностью , которая подается после сброса в . Если B проходит все тесты для всех , тогда B подобен A. Эта часть теста проверяет все переходы остовного дерева. В конце мы проверяем переходы, не входящие в дерево. Для каждого перехода, скажем из 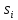в через a, мы делаем тоже самое для каждого члена : сбрасываем автомат, подаем последовательность , переводящая автомат в , подаем на вход a, и затем подаем разделяющую последовательность из . 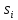Если автомат-реализация B проходит этот тест для всех , тогда переход состояния, подобное , под действием a выдает корректную последовательность и переходит в состояние подобное . Если B проходит этот тест для всех переходов, тогда мы объявляем его изоморфным A.

Пример 3: Для автомата на рис.1, семейство разделяющих последовательностей представляет собой: 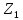={a,b}, ={a}, и ={a,b}. Остовное дерево показано на рис.9 жирными ребрами. Последовательности ra и rb проверяют состояние . Последовательность rba проверяет и переход (s1,s2): после сброса, вход b проверяет переход по ребру дерева из в и разделяющая последовательность из проверяет конечное состояние . Следующие последовательности проверяют состояние и переход из в : rbba и rbbb, где префикс rbb сбрасывает автомат в и переводит в состояние вдоль проверенных ребер, а два суффикса a и b разделяющие последовательности для . В конце мы тестируем ребра не из дерева таким же образом. Например, петля при проверяется последовательностью rbaa.

Проверка B на подобие занимает время: O() – на постройку семейства разделяющих последовательностей, O(pn) – построить остовное дерево, O()- проверить состояние и ребра дерева, и O() – проверить переход и его конечное состояние. Всего переходов pn, таким образом, тестовая последовательность длины O() строится за время O().

Для автоматов с ненадежным сбросом известны лишь случайные полиномные алгоритмы, они строят тестовые последовательности длины за случайное полиномное время.