2.1 Различимость, изоморфизм и минимизация.

Два состояния и неразличимы тогда и только тогда, когда для каждой входной последовательности автомат будет выдавать одинаковый сигнал, независимо от того, какое состояние является начальным или , т.е. для любой входной последовательности x справедливо, что 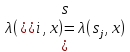, иначе два состояния разичимы, если существует входная последовательность x, для которой. Такая последовательность называется разделяющая последовательностью. Для двух состояний в разных автоматах с одинаковыми входными и выходными алфавитами определение такое же. Два автомата M и M’ эквивалентны тогда и только тогда, когда для каждого состояния из M существует неразличимое состояние из M’ . Пусть M=(I,O,S,) и M’=(I,O,S’,) два автомата с общим входным и выходным алфавитами. Гомеоморфизм из M в M’ это отображение такое, что для каждого состояния и для каждого входного сигнала aсправедливо, что и . Если -биекция, то такое отношение называется изоморфизмом, в этом случае M и M’ должны иметь одинаковое количество состояний идентичных друг другу с учетом возможного переименования. Два автомата называются изоморфными, если существует изоморфизм из одного в другой. Очевидно, два изоморфных конечных автомата эквивалентны друг другу, обратное строго говоря неверно.

В классе эквивалентных автоматов находятся все автоматы с одинаковым вход-выходным поведением, т.е. на каждый сигнал все эти автоматы выдают одинаковые сигналы. В каждом классе эквивалентности есть автомат с минимальным количеством состояний, называющийся минимальным. Автомат минимизирован тогда и только тогда, когда в автомате нет эквивалентных состояний. В классе эквивалентности любые два минимизированных автомата имеют одинаковое количество состояний, к тому же биективное отображение состояний обуславливает изоморфизм данных автоматов. Таким образом, минимальный автомат в классе эквивалентности определен с точностью до изоморфизма.

Если дан автомат M, то мы можем найти минимизированный, эквивалентный ему автомат следующим образом. Эквивалентные друг другу состояния образуют блок, мы можем разбить множество состояний на такие блоки. Сначала проводим разбиение по выходным сигналам, т.е. два состояния принадлежат одному блоку тогда и только тогда, когда на каждый входной сигнал, выходные сигналы совпадают. Когда все состояния распределены по блокам, делим блоки на подблоки по переходам, т.е. два состояния входят в один подблок, если на каждый входной сигнал они переходят в одно и то же состояние. Повторяем данный процесс пока все состояния не будут полностью распределены, т.е. каждый блок содержит в себе эквивалентные состояния и состояния в разных блоках не эквивалентны друг другу. Вдобавок, для состояний в разных блоках последовательность входных сигналов, участвующая в их разделении есть разделяющая последовательность. За один круг деления мы проверяем все p входных сигналов для каждого из n состояний, а всего таких кругов не больше, чем n-1, для n состояний. Сложность такого разбиения равна O(p). Модификация алгоритма дает сложность ).

После разбиения состояний на блоки, получим r блоков:, можем построить минимизированный автомат M’. Мы сопоставляем каждому блоку состояние: и множество состояний S’ автомата M’: . Переопределим функции выходов и переходов. Под действием входного сигнала a все состояния блока переходят в блок и подают на выход сигнал o. Тогда и . В M’ нет неразличимых состояний и он эквивалентен автомату M. Заметим, что M’ есть гомоморфное отображение M (и всех автоматов в классе эквивалентности M). Гомоморфизм переводит все состояния из в соответствующее состояние .