
- •1. Введение.
- •2. Основные определения.
- •2.1 Различимость, изоморфизм и минимизация.
- •2.2 Проблемы тестирования.
- •2.3 Установочная последовательность.
- •2.4 Синхронизирующие последовательности.
- •3. Идентификация и верификация состояния.
- •3.2. Простые условные диагностические эксперименты.
- •3.3. Построение простого условного диагностического эксперимента.
- •3.4. Верификация состояния.
- •4. Тест На Соответствие.
- •4.1. Статусные Сообщения и Сброс.
- •4.2. Разделяющие Последовательности.
- •5. Вывод.
- •6. Список литературы
- •7.Приложение.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
имени М.В. ЛОМОНОСОВА
Механико-математический факультет
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
Об эффективной реализации экспериментов
с конечными автоматами.
Автор:
Студент 4 курса, 412 группы ______________________Оспанов Б.П.
Научный руководитель:
к.ф.-м.н., доцент ______________________________Пантелеев П.А.
Рецензент:
к.ф.-м.н., с.н.с_________________________________Галатенко А.В
Москва 2015 г.
Содержание:
1. Введение ……………………………………………………………………………………………………………………..3
2. Основные определения………………………………………………………………………………………………. 4
2.1. Различимость, изоморфизм и минимизация ………………………………………………………….6
2.2 Проблемы тестирования ……………………………………………………………………………………………7
2.3 Установочная последовательность ………………………………………………………………………. 8
2.4 Синхронизирующие последовательности…………………………………………………………………9
3. Идентификация и верификация состояния………………………………………………………………….10
3.1. Простые безусловные диагностические эксперименты.………………………………………..11
3.2. Простые условные диагностические эксперименты ….…………………………………………..12
3.3. Построение простого условного диагностического эксперимента.……………………….13
3.4. Верификация состояния…………………………………………………………………………………………….15
4. Тест на соответствие……………………………………………………………………………………………………….16
4.1. Статусные сообщения и сброс…………………………………………………………………………………..18
4.2. Разделяющие последовательности……………………………………………………………………….…19
5. Вывод……………………………………………………………………………………………………………………………...22
6. Список литературы ………………………………………………………………………………………………………..23
7.Приложение……………………………………………………………………………………………………………………..24
1. Введение.
Конечные автоматы широко используются для моделирования систем в различных областях, включая последовательные схемы, некоторые программы (лексический анализ, сопоставление с образцом и т.д.) и совсем недавно в протоколах связи. Потребность в повышении надежности систем требует изучения проблем тестирования автоматов, чтобы обеспечить корректное функционирование и узнать аспекты их поведения.
Есть 2 вида конечных автоматов: автомат Мили и автомат Мура. Здесь мы рассматриваем модель Мили, т.к. она более удобна для следующих высказываний и является более распространенной, чем модель Мура.
Рассматривается 2 вида проблем тестирования. В первом случае мы имеем диаграмму переходов конечного автомата, но не знаем в каком состоянии он находится. На вход автомату подается последовательность, анализируя вход-выходные данные, получаем информацию о текущем состоянии. В проблеме идентификации состояния нас волнует определение начального состояния автомата. Тестовая последовательность, которая решает эту проблему, называется простым диагностическим экспериментом.
Проблема верификации состояния отвечает на вопрос, в каком состоянии сейчас находится автомат. Тестовая последовательность, которая решает эту проблему, называется уникальная вход-выходная (УВВ) последовательность.
Второй тип проблем тестирования это проверка на соответствие. Нам дан автомат-эталон, для которого известна его диаграмма переходов и дан автомат (который нужно проверить на соответствие), для которого мы можем наблюдать только его вход-выходное поведение. Нужно проверить, соответствует ли данный автомат автомату-эталону. Последовательность, решающая эту проблему, называется тестовой последовательностью.
2. Основные определения.
Cначала, мы представим главные определения: неразличимые состояния и автоматы, изоморфизм, минимизация.
Опр.1 Конечный автомат M это пятерка:
M=(I,O,S,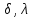 ),
),
Где
I,O
и S
конечные и непустые множества входного
алфавита, выходного алфавита и состояний,
соответственно.
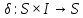 - функция переходов,
- функция переходов,
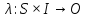 - функция выходов.
- функция выходов.
Если
автомат находится в состоянии s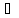 S
и получает на вход сигнал a
S
и получает на вход сигнал a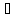 I,
то автомат переходит в состояние
I,
то автомат переходит в состояние
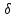 (s,a)
и подает на выход сигнал
(s,a)
и подает на выход сигнал
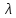 (s,a).
(s,a).
Конечный
автомат может быть представлен в виде
диаграммы переходов: направленный граф,
вершины которого отвечают за состояния,
а грани за переходы между состояниями,
на них отмечены входные и выходные
сигналы. Для конечного автомата на
рис.1, предположим, что он находится в
состоянии
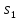 .Под
действием сигнала b
автомат переходит в состояние
.Под
действием сигнала b
автомат переходит в состояние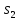 и выдает сигнал 1. Точно также конечный
автомат может быть представлен таблицей
состояний: в первом столбце находятся
все состояния, в каждом следующем столбце
указано, куда перейдет автомат и что
подаст на выход и так для каждого входного
сигнала. Как на таблице 1, которая
определяет диаграмму переходов на
рис.1.
и выдает сигнал 1. Точно также конечный
автомат может быть представлен таблицей
состояний: в первом столбце находятся
все состояния, в каждом следующем столбце
указано, куда перейдет автомат и что
подаст на выход и так для каждого входного
сигнала. Как на таблице 1, которая
определяет диаграмму переходов на
рис.1.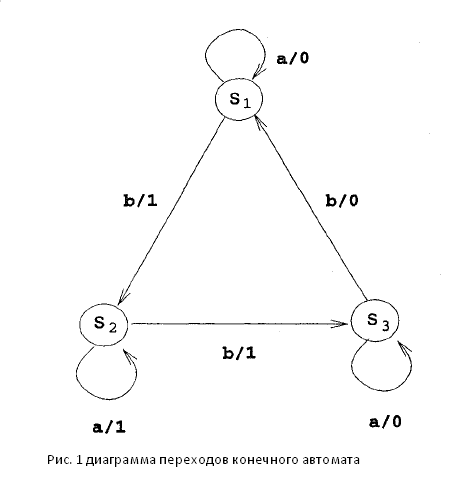
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
таблица 1.
Определим
количество элементов во множествах:
n=|S|,
p=|I|,
q=|O|.
Определим функции переходов и выходов
для последовательностей. Для начального
состояния
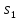 входная последовательность x=
входная последовательность x= проводит
автомат в состояния:
проводит
автомат в состояния:
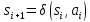 ,
i=1,…..,k
и в финальное
,
i=1,…..,k
и в финальное
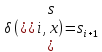 .
Получаем выходную последовательность
.
Получаем выходную последовательность
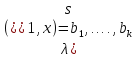 ,
где
,
где
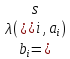 ,
i=1,…,k.
Для автомата на рис.1 входная
последовательность abb
переводит его в состояния
,
i=1,…,k.
Для автомата на рис.1 входная
последовательность abb
переводит его в состояния
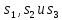 и выводит 011. Также функции переходов и
выходов можно расширить на множества:
и выводит 011. Также функции переходов и
выходов можно расширить на множества:
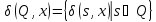 и
и
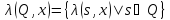 .
.
Входная
последовательность x
индуцирует разбиение
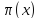 множества состояний S,
где два состояния
множества состояний S,
где два состояния
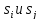 находятся в одном блоке тогда и только
тогда, когда они не различимы
последовательностью x,
т.е.
находятся в одном блоке тогда и только
тогда, когда они не различимы
последовательностью x,
т.е.
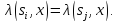 Такое разбиение называется неопределенность
начального состояния последовательности
x.
Заметим, что после подачи входной
последовательности x
в M
и обзора выходной последовательности,
информация о начальном состоянии,
которую мы получим это блок
Такое разбиение называется неопределенность
начального состояния последовательности
x.
Заметим, что после подачи входной
последовательности x
в M
и обзора выходной последовательности,
информация о начальном состоянии,
которую мы получим это блок
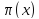 ,
к которому принадлежит выходная
последовательность. Информация о текущем
состоянии автомата M,
в котором он находится после подачи
входной последовательности x,
хранится в семействе множеств:
,
к которому принадлежит выходная
последовательность. Информация о текущем
состоянии автомата M,
в котором он находится после подачи
входной последовательности x,
хранится в семействе множеств:
 ,
называющееся неопределенностью текущего
состояния последовательности x.
Заметим, что
,
называющееся неопределенностью текущего
состояния последовательности x.
Заметим, что
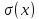 не обязательно является разбиением,
т.е. множества в
не обязательно является разбиением,
т.е. множества в
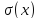 могут пересекаться. Выходной сигнал
произведенный автоматом M,
в ответ на входной сигнал, указывает на
то, какому множеству семейства
могут пересекаться. Выходной сигнал
произведенный автоматом M,
в ответ на входной сигнал, указывает на
то, какому множеству семейства
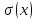 принадлежит текущее состояние. Например,
для автомата на рис.1 подаем на вход b.
Если на выход получим 1, значит начальным
состоянием могло быть
принадлежит текущее состояние. Например,
для автомата на рис.1 подаем на вход b.
Если на выход получим 1, значит начальным
состоянием могло быть
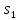 или
или
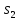 ,
а текущим состоянием
,
а текущим состоянием
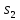 или
или
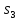 ,
если получим 0, то значит, начальным
состоянием было
,
если получим 0, то значит, начальным
состоянием было
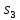 ,
а текущее
,
а текущее
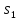 .
Таким образом, для сигнала b
неопределенность
начального состояния :
.
Таким образом, для сигнала b
неопределенность
начального состояния :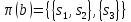 и неопределенность текущего состояния:
и неопределенность текущего состояния:
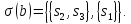
Дерево
преемников автомата - это дерево,
показывающее поведение автомата,
начинающего работу в любой из вершин
под действием любой последовательности.
Для каждой входной последовательности
дерево содержит в себе путь, который
берет начало в корне дерева и каждая
вершина обозначена соответствующим
текущим (начальным) состоянием
неопределенности. На рис.2 показано
дерево преемников автомата на рис.1.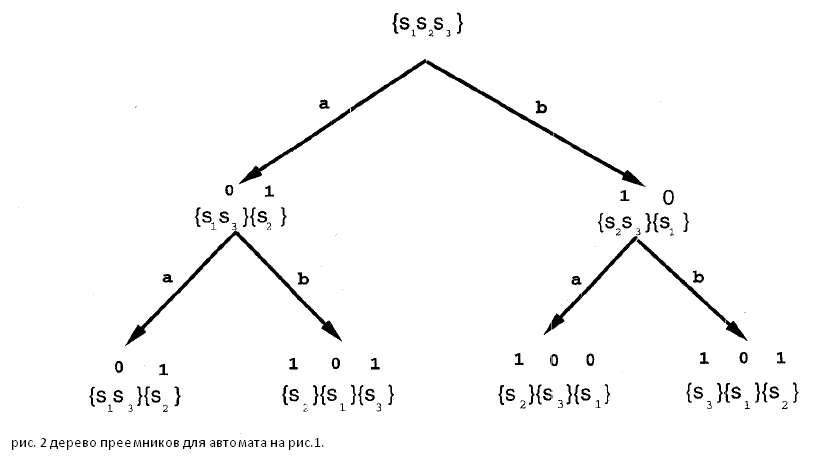
Таким
образом, корень обозначен всем набором
состояний, правый потомок обозначен: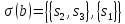 с
соответствующими выходами
с
соответствующими выходами
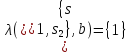 и
и
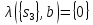 и т.д.
и т.д.
Диаграмма переходов конечного автомата - это направленный граф. Таким образом, теория графов применима в анализе конечных автоматов. Например, мы хотим найти кратчайший путь между двумя вершинами, при этом находим кратчайшую последовательность, переводящую автомат из одного состояния в другое. Также, мы можем найти путь, который проходит по каждому ребру единожды.
Конечный автомат в определении 1 полностью определен в том отношении, что при подаче входного сигнала в автомат, следующее состояние определено функцией переходов, а выходной сигнал определен функцией выходов. Иначе, автомат определен не полностью, т.е. для некоторых состояний при некоторых сигналах функции переходов и выходов не определены. Также, автомат является детерминированным, если под действием входного сигнала автомат переходит в определенное состояние. Иначе, автомат недетерминированный, т.е. он может переходить в несколько состояний под действием определенного символа, а выход будет различаться. Далее будем рассматривать полностью определенные детерминированные конечные автоматы.

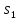
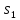 ,0
,0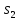 ,1
,1
 ,1
,1 ,1
,1
 ,0
,0 ,1
,1